2022~2023学年中考数学一轮复习专题17圆中角度长度计算问题
试卷更新日期:2022-12-14 类型:一轮复习
一、角度问题
-
1. 如图, 内接于 ,CD是 的直径, ,则 ( )
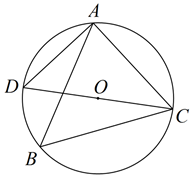 A、70° B、60° C、50° D、40°2. 如图,A、B、C点在圆O上, 若∠ACB=36°, 则∠AOB= .
A、70° B、60° C、50° D、40°2. 如图,A、B、C点在圆O上, 若∠ACB=36°, 则∠AOB= .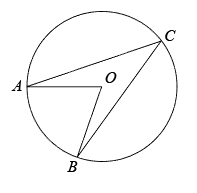 3. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .4. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.
3. 已知⊙O的直径AB长为2,弦AC长为 , 那么弦AC所对的圆周角的度数等于 .4. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.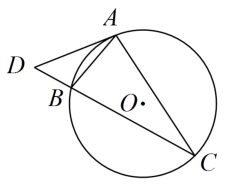 5. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
5. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )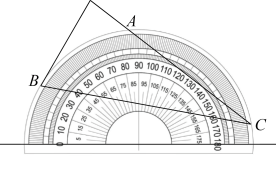 A、28° B、30° C、36° D、56°6. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )
A、28° B、30° C、36° D、56°6. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )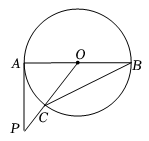 A、25° B、35° C、40° D、50°7. 如图,点A,B,C在 上, ,则 度.
A、25° B、35° C、40° D、50°7. 如图,点A,B,C在 上, ,则 度. 8. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )
8. 如图,AB,CD是的弦,延长AB,CD相交于点P.已知 , , 则的度数是( )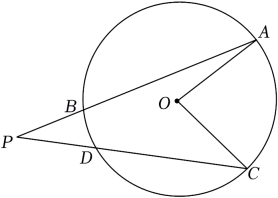 A、30° B、25° C、20° D、10°9. 如图,四边形是的内接四边形.若 , 则的度数为( )
A、30° B、25° C、20° D、10°9. 如图,四边形是的内接四边形.若 , 则的度数为( )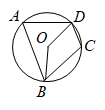 A、138° B、121° C、118° D、112°10. 如图,⊙是的外接圆,是⊙的直径,点P在⊙上,若 , 则的度数是( )
A、138° B、121° C、118° D、112°10. 如图,⊙是的外接圆,是⊙的直径,点P在⊙上,若 , 则的度数是( )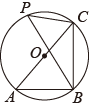 A、 B、 C、 D、11. 如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为 .
A、 B、 C、 D、11. 如图,∠DCE是⊙O内接四边形ABCD的一个外角,若∠DCE=72°,那么∠BOD的度数为 .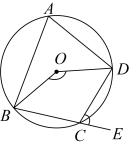 12. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( )
12. 如图,由边长为1的小正方形构成的网格中,点 , , 都在格点上,以为直径的圆经过点 , , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、长度问题
-
13. 如图,为的直径,弦交于点 , , , , 则( )
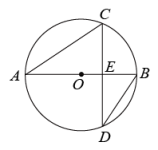 A、 B、 C、1 D、214. 如图,点A,C,D,B在⊙O上,AC=BC,∠ACB=90°.若CD=a,tan∠CBD= , 则AD的长是 .
A、 B、 C、1 D、214. 如图,点A,C,D,B在⊙O上,AC=BC,∠ACB=90°.若CD=a,tan∠CBD= , 则AD的长是 .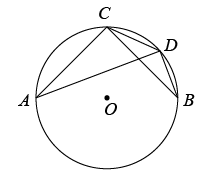 15. 如图,是的内接三角形.若 , , 则的半径是.
15. 如图,是的内接三角形.若 , , 则的半径是.
三、切线长问题
-
16. 四边形内接于 , 直径与弦交于点 , 直线与相切于点 .
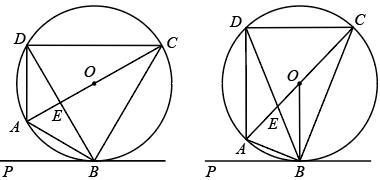 (1)、如图1,若 , 且 , 求证:平分;(2)、如图2,连接 , 若 , 求证: .17. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.
(1)、如图1,若 , 且 , 求证:平分;(2)、如图2,连接 , 若 , 求证: .17. 如图,已知BC为⊙O的直径,点D为的中点,过点D作DG∥CE,交BC的延长线于点A,连接BD,交CE于点F.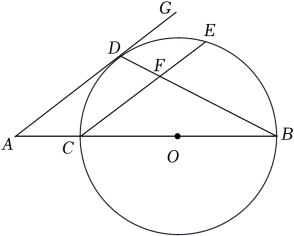 (1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.18. 如图,以线段为直径作 , 交射线于点 , 平分交于点 , 过点作直线于点 , 交的延长线于点 . 连接并延长交于点 .
(1)、求证:AD是⊙O的切线;(2)、若EF=3,CF=5,tan∠GDB=2,求AC的长.18. 如图,以线段为直径作 , 交射线于点 , 平分交于点 , 过点作直线于点 , 交的延长线于点 . 连接并延长交于点 .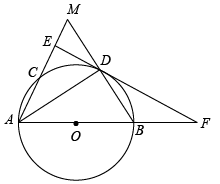 (1)、求证:直线是的切线;(2)、求证:;(3)、若 , , 求的长.19. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M.
(1)、求证:直线是的切线;(2)、求证:;(3)、若 , , 求的长.19. 如图,在Rt△ABC中,∠B=90°,AE平分∠BAC交BC于点E,O为AC上一点,经过点A、E的⊙O分别交AB、AC于点D、F,连接OD交AE于点M. (1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.20. 如图, 是 的外接圆,AB是直径, ,连接AD, ,AC与OD相交于点E.
(1)、求证:BC是⊙O的切线.(2)、若CF=2,sinC= , 求AE的长.20. 如图, 是 的外接圆,AB是直径, ,连接AD, ,AC与OD相交于点E. (1)、求证:AD是 的切线;(2)、若 , ,求 的半径.21. 如图,已知 是 的直径,点 是 上异于 , 的点,点 是 的中点,连接 , , ,过点 作 交 的延长线于点 ,交 的延长线于点 , 的平分线 交 于点 ,交 于点 .
(1)、求证:AD是 的切线;(2)、若 , ,求 的半径.21. 如图,已知 是 的直径,点 是 上异于 , 的点,点 是 的中点,连接 , , ,过点 作 交 的延长线于点 ,交 的延长线于点 , 的平分线 交 于点 ,交 于点 . (1)、求证: 是 的切线;(2)、求 的值;(3)、若 , ,求 的直径.22. 如图,AB是⊙O的直径,E为⊙O上的一点,∠ABE的平分线交⊙O于点C,过点C的直线交BA的延长线于点P,交BE的延长线于点D.且∠PCA=∠CBD.
(1)、求证: 是 的切线;(2)、求 的值;(3)、若 , ,求 的直径.22. 如图,AB是⊙O的直径,E为⊙O上的一点,∠ABE的平分线交⊙O于点C,过点C的直线交BA的延长线于点P,交BE的延长线于点D.且∠PCA=∠CBD.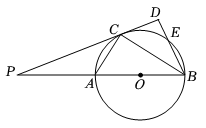 (1)、求证:PC为⊙O的切线;(2)、若PC=BO,PB=12,求⊙O的半径及BE的长.23. 如图,在 中, .以AB为直径的 与线段BC交于点D,过点D作 ,垂足为E,ED的延长线与AB的延长线交于点P.
(1)、求证:PC为⊙O的切线;(2)、若PC=BO,PB=12,求⊙O的半径及BE的长.23. 如图,在 中, .以AB为直径的 与线段BC交于点D,过点D作 ,垂足为E,ED的延长线与AB的延长线交于点P. (1)、求证:直线PE是 的切线;(2)、若 的半径为6, ,求CE的长.
(1)、求证:直线PE是 的切线;(2)、若 的半径为6, ,求CE的长.四、阴影面积问题
-
24. 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°.
 (1)、求:∠CAD的度数;(2)、若AD=6,求图中阴影部分的面积.25. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD.
(1)、求:∠CAD的度数;(2)、若AD=6,求图中阴影部分的面积.25. 如图,C,D是以AB为直径的半圆上的两点, , 连结BC,CD. (1)、求证: .(2)、若 , , 求阴影部分的面积.26. 如图,四边形内接于 , 为的直径,平分 , 点E在的延长线上,连接 .
(1)、求证: .(2)、若 , , 求阴影部分的面积.26. 如图,四边形内接于 , 为的直径,平分 , 点E在的延长线上,连接 . (1)、求直径的长;(2)、若 , 计算图中阴影部分的面积.27. 如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.
(1)、求直径的长;(2)、若 , 计算图中阴影部分的面积.27. 如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.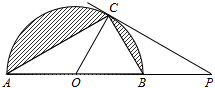 (1)、求证:∠ACO=∠BCP;(2)、若∠ABC=2∠BCP,求∠P的度数;(3)、在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).28. 如图,AB是半圆O的直径,点C在半圆O上,点D为的中点,连接AC,BC,AD,AD与BC相交于点G,过点D作直线DEBC,交AC的延长线于点E.
(1)、求证:∠ACO=∠BCP;(2)、若∠ABC=2∠BCP,求∠P的度数;(3)、在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).28. 如图,AB是半圆O的直径,点C在半圆O上,点D为的中点,连接AC,BC,AD,AD与BC相交于点G,过点D作直线DEBC,交AC的延长线于点E.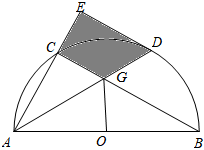 (1)、求证:DE是⊙O的切线;(2)、若 , CG=2 , 求阴影部分的面积.29. 如图,在中, , 以为圆心,的长为半径的圆交边于点 , 点在边上且 , 延长交的延长线于点 .
(1)、求证:DE是⊙O的切线;(2)、若 , CG=2 , 求阴影部分的面积.29. 如图,在中, , 以为圆心,的长为半径的圆交边于点 , 点在边上且 , 延长交的延长线于点 . (1)、求证:是圆的切线;(2)、已知 , , 求长度及阴影部分面积.
(1)、求证:是圆的切线;(2)、已知 , , 求长度及阴影部分面积.五、圆相关尺规作图
-
30. 证明:垂直于弦的直径平分弦以及弦所对的两条弧.
 31. 如图,⊙O是△ABC的外接圆,∠ABC=45°.
31. 如图,⊙O是△ABC的外接圆,∠ABC=45°.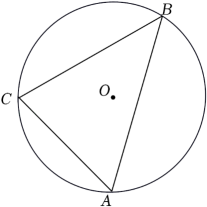 (1)、请用尺规作出⊙O的切线AD(保留作图痕迹,不写作法);(2)、在(1)的条件下,若AB与切线AD所夹的锐角为75°,⊙O的半径为2,求BC的长.32. 如图,的内切圆(圆心为点O)与各边分别相切于点D,E,F,连接 . 以点B为圆心,以适当长为半径作弧分别交于G,H两点;分别以点G,H为圆心,以大于的长为半径作弧,两条弧交于点P;作射线 . 下列说法正确的是( )
(1)、请用尺规作出⊙O的切线AD(保留作图痕迹,不写作法);(2)、在(1)的条件下,若AB与切线AD所夹的锐角为75°,⊙O的半径为2,求BC的长.32. 如图,的内切圆(圆心为点O)与各边分别相切于点D,E,F,连接 . 以点B为圆心,以适当长为半径作弧分别交于G,H两点;分别以点G,H为圆心,以大于的长为半径作弧,两条弧交于点P;作射线 . 下列说法正确的是( ) A、射线一定过点O B、点O是三条中线的交点 C、若是等边三角形,则 D、点O不是三条边的垂直平分线的交点33. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )
A、射线一定过点O B、点O是三条中线的交点 C、若是等边三角形,则 D、点O不是三条边的垂直平分线的交点33. 如图,在△ABC中,BD平分∠ABC,以点A为圆心,以任意长为半径画弧交射线AB,AC于两点,分别以这两点为圆心,以适当的定长为半径画弧,两弧交于点E,作射线AE,交BD于点I,连接CI,以下说法错误的是( )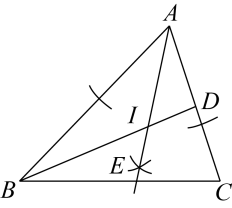 A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等34. 操作探究题(1)、已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.
A、I到AB,AC边的距离相等 B、CI平分∠ACB C、I是△ABC的内心 D、I到A,B,C三点的距离相等34. 操作探究题(1)、已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.操作:如图1,分别将半圆的圆心角(取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);

交流:当时,可以仅用圆规将半圆的圆心角所对的弧三等分吗?
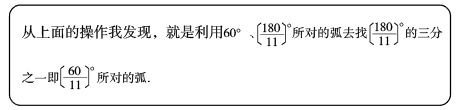
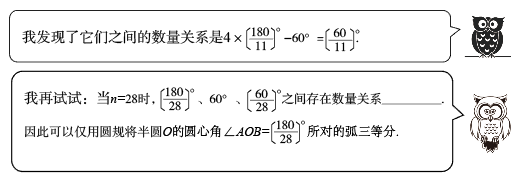
探究:你认为当满足什么条件时,就可以仅用圆规将半圆的圆心角所对的弧三等分?说说你的理由.
(2)、如图2,的圆周角 . 为了将这个圆的圆周14等分,请作出它的一条14等分弧(要求:仅用圆规作图,不写作法,保留作图痕迹).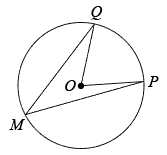
六、正多边形与圆
-
35. 如图,已知的半径为1,则它的内接正方形的边长为( )
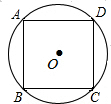 A、 B、2 C、1 D、36. 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )
A、 B、2 C、1 D、36. 如图,已知⊙O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )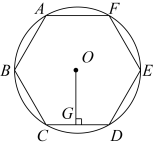 A、3 B、 C、 D、337. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )
A、3 B、 C、 D、337. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( ) A、 B、 C、 D、38. 如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.
A、 B、 C、 D、38. 如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度”.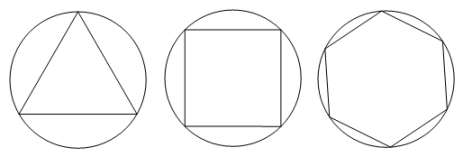 (1)、角的“接近度”定义:设正n边形的每个内角的度数为 , 将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,
(1)、角的“接近度”定义:设正n边形的每个内角的度数为 , 将正n边形的“接近度”定义为.于是越小,该正n边形就越接近于圆,①若 , 则该正n边形的“接近度”等于.
②若 , 则该正n边形的“接近度”等于.
③当“接近度”等于.时,正n边形就成了圆.
(2)、边的“接近度”定义:设一个正n边形的外接圆的半径为R,正n边形的中心到各边的距离为d,将正n边形的“接近度”定义为.分别计算时边的“接近度”,并猜测当边的“接近度”等于多少时,正n边形就成了圆?