(苏科版)2022-2023学年九年级数学下册7.6 用锐角三角函数解决问题 同步测试
试卷更新日期:2022-12-14 类型:同步测试
一、单选题
-
1. 如图,在Rt△ABC中,∠C=90°,BC= , 点D是AC上一点,连接BD.若tanA= , tan∠ABD= , 则CD的长为( )
 A、2 B、3 C、2 D、2. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )
A、2 B、3 C、2 D、2. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )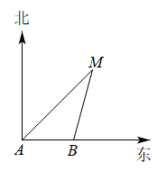 A、海里 B、海里 C、40海里 D、海里3. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )
A、海里 B、海里 C、40海里 D、海里3. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )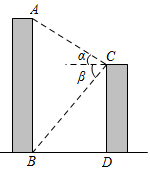 A、 B、 C、 D、4. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比是1∶ , 则AC的长是( )
A、 B、 C、 D、4. 河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比是1∶ , 则AC的长是( ) A、6米 B、12米 C、3米 D、6米5. 如图,河坝横断面迎水坡的坡比为: , 坝高m,则的长度为( )
A、6米 B、12米 C、3米 D、6米5. 如图,河坝横断面迎水坡的坡比为: , 坝高m,则的长度为( )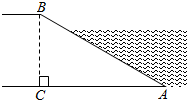 A、6m B、m C、9m D、m6. 如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡AB的坡度i=1:2.5,则此斜坡的水平距离AC为( )
A、6m B、m C、9m D、m6. 如图,有一斜坡AB,坡顶B离地面的高度BC为30m,斜坡AB的坡度i=1:2.5,则此斜坡的水平距离AC为( )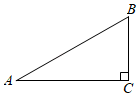 A、75m B、50m C、30m D、12m7. 如图,一艘海轮位于灯塔的北偏东55°方向的处,已知海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离的长是( )
A、75m B、50m C、30m D、12m7. 如图,一艘海轮位于灯塔的北偏东55°方向的处,已知海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离的长是( )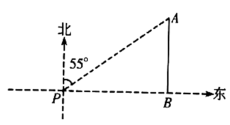 A、6海里 B、海里 C、海里 D、海里8. 某简易房的示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AC的长为( )
A、6海里 B、海里 C、海里 D、海里8. 某简易房的示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AC的长为( )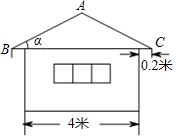 A、米 B、米 C、米 D、米9. 如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m的高空C处时,测得A处渔政船的俯角为45°,测得B处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB是( )
A、米 B、米 C、米 D、米9. 如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m的高空C处时,测得A处渔政船的俯角为45°,测得B处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB是( ) A、m B、m C、m D、m10. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )
A、m B、m C、m D、m10. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )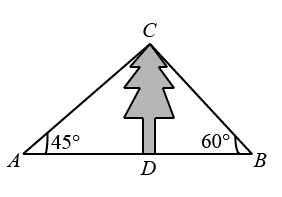 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图是一种机器零件的示意图,其中米,米,则四边形的面积为米2
 12. 小丽想测量学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为30°,测倾器到旗杆底部的距离为12米,测倾器的高度为1.6米,那么旗杆的高度为米(结果保留根号).
12. 小丽想测量学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为30°,测倾器到旗杆底部的距离为12米,测倾器的高度为1.6米,那么旗杆的高度为米(结果保留根号). 13. 如图,A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,小明同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时小明同学一共走的距离为米.
13. 如图,A位于学校主教学楼P南偏东45°方向,且距离教学楼60米,小明同学从这里出发沿着正北方向走了一段时间后,到达位于主教学楼北偏东30°方向的综合楼B处,此时小明同学一共走的距离为米. 14. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )
14. 一艘轮船位于灯塔的南偏东方向,距离灯塔30海里的处,它沿北偏东方向航行一段时间后,到达位于灯塔的北偏东方向上的处,此时与灯塔的距离约为海里.(参考数据: , , )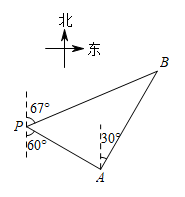 15. 如图,河堤横断面迎水坡的坡比是 , 堤高 , 则坡面的长度是m.
15. 如图,河堤横断面迎水坡的坡比是 , 堤高 , 则坡面的长度是m.
三、解答题
-
16. 如图,AD是△ABC中BC边上的高,且∠B=30°,∠C=45°,CD=2.求BC的长.
 17. 某学校升气球庆祝党的二十大胜利召开.如图,一气球到达离地面高度为12米的处时,仪器显示正前方一高楼顶部的仰角是 , 底部的俯角是 . 气球要飞到楼顶,应至少再上升多少米?(结果精确到0.1米)(参考数据: , , , )
17. 某学校升气球庆祝党的二十大胜利召开.如图,一气球到达离地面高度为12米的处时,仪器显示正前方一高楼顶部的仰角是 , 底部的俯角是 . 气球要飞到楼顶,应至少再上升多少米?(结果精确到0.1米)(参考数据: , , , )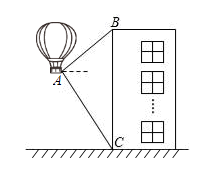 18. 如图,某港口O位于南北延伸的海岸线上,东面是大海.远洋号、长峰号两艘轮船同时离开港O,“远洋”号沿着北偏东60°方向航行,“长峰”号沿着南偏东30°方向匀速航行,“远洋”号每小时航行12海里,“长峰”号每小时航行16海里,它们离开港口1小时后,分别到达A,B两个位置,求1小时后远洋号、长峰号两艘轮船相距多少海里.
18. 如图,某港口O位于南北延伸的海岸线上,东面是大海.远洋号、长峰号两艘轮船同时离开港O,“远洋”号沿着北偏东60°方向航行,“长峰”号沿着南偏东30°方向匀速航行,“远洋”号每小时航行12海里,“长峰”号每小时航行16海里,它们离开港口1小时后,分别到达A,B两个位置,求1小时后远洋号、长峰号两艘轮船相距多少海里.
四、综合题
-
19. 如图,已知∠ABC和射线BD上一点P(点P与点B不重合),且点P到BA.BC的距离为PE、PF.
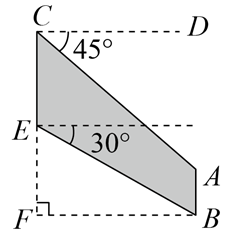
 (1)、若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;(2)、若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.20. 图1是停车场入口处的升降杆,当汽车刷牌照进入时,升降杆就会从水平位置升起.图2是其示意图,其中 , , , , , 现由于故障,不能完全升起,最大为 .
(1)、若∠EBP=40°,∠FBP=20°,PB=m,试比较PE、PF的大小;(2)、若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β.试判断PE、PF的大小,并给出证明.20. 图1是停车场入口处的升降杆,当汽车刷牌照进入时,升降杆就会从水平位置升起.图2是其示意图,其中 , , , , , 现由于故障,不能完全升起,最大为 .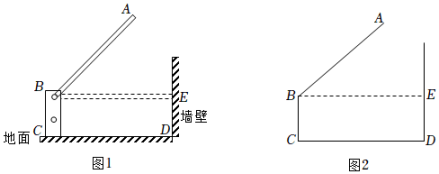 (1)、求故障时A点最高可距离地面多少m(精确到0.1m).(2)、若一辆箱式小货车宽1.8m,高2.4m,请问这辆车能否在升降杆故障时进入停车场?
(1)、求故障时A点最高可距离地面多少m(精确到0.1m).(2)、若一辆箱式小货车宽1.8m,高2.4m,请问这辆车能否在升降杆故障时进入停车场?(参考数据: , , )
21. 九年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A处向正北方向走了220米,到达菜园B处锄草,再从B处沿正西方向走了200米,到达果园C处采摘水果,再向南偏东37°方向走了200米,到达手工坊D处进行手工制作,最后从D处回到门口A处. (1)、求从手工坊D处回到门口A处的距离.(2)、求从手工坊D处回到门口A处的方位角.[参考数据: , , ]22. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,)
(1)、求从手工坊D处回到门口A处的距离.(2)、求从手工坊D处回到门口A处的方位角.[参考数据: , , ]22. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄BC与手臂MC始终在同一直线上,枪身BA与额头保持垂直.量得胳膊MN=28cm,MB=42cm,肘关节M与枪身端点A之间的水平宽度为25.3cm(即MP的长度),枪身BA=8.5cm.(参考数据:sin66.4°≈0.92,cos66.4°≈0.40,sin23.6°≈0.40,) (1)、求∠ABC的度数;(2)、测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)23. 如图,在坡顶A处的同一水平面上有一座网络信号塔 , 数学兴趣小组的同学在斜坡底处测得该塔的塔顶的仰角为45°,然后他们沿着坡度为1:2.4的斜坡攀行了26米到达坡顶,在坡顶A处又测得该塔的塔顶的仰角为76°.求:
(1)、求∠ABC的度数;(2)、测温时规定枪身端点A与额头距离范围为3~5cm.在图2中,若测得∠BMN=68.6°,小红与测温员之间距离为50cm.问此时枪身端点A与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)23. 如图,在坡顶A处的同一水平面上有一座网络信号塔 , 数学兴趣小组的同学在斜坡底处测得该塔的塔顶的仰角为45°,然后他们沿着坡度为1:2.4的斜坡攀行了26米到达坡顶,在坡顶A处又测得该塔的塔顶的仰角为76°.求: (1)、坡顶A到地面的距离;(2)、网络信号塔的高度(结果精确到0.1米).(参考数据: , , )
(1)、坡顶A到地面的距离;(2)、网络信号塔的高度(结果精确到0.1米).(参考数据: , , )