（苏科版）2022-2023学年九年级数学下册7.5 解直角三角形同步测试

试卷更新日期：2022-12-14 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，AB是⊙O的直径，且经过弦CD的中点H，已知cos∠CDB＝ $\frac{4}{5}$ ， BD＝5，则OH的长为（）

A、 $\frac{2}{3}$ B、 $\frac{5}{6}$ C、1 D、 $\frac{7}{6}$

查看试题解析
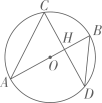2. 在 $Rt △ ABC$ 中，∠C= $90^{°}$ ，AB=4， $tanA = \sqrt{3}$ ，则 $BC$ 的长为（）

A、3 B、2 C、 $\sqrt{3}$ D、 $2 \sqrt{3}$

查看试题解析
3. 如图，在△ABC中，∠C＝90°，∠A＝30°，BD为△ABC的角平分线，若AC＝12，则在△ABD中AB边上的高为（）

A、3 B、4 C、5 D、6

查看试题解析
4. 在Rt△ABC中，∠C=90°，AB=5，AC=4．下列四个选项，正确的是（）

A、tanB= $\frac{3}{4}$ B、sinB= $\frac{4}{3}$ C、sinB= $\frac{4}{5}$ D、cosB= $\frac{4}{5}$

查看试题解析
5. 如图，菱形ABCD中，AB＝2，∠A＝120°，点P、Q、K分别为线段BC、CD、BD上任意一点，则PK+QK的最小值为（）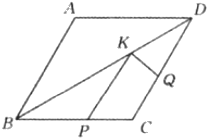

A、1 B、 $\sqrt{3}$ C、2 D、 $\sqrt{3} +$ 1

查看试题解析
6. 如图，在 Rt△ABC 中，∠C＝90°，∠B＝30°，AB＝8，则 BC 的长是（）

A、 $\frac{4 \sqrt{3}}{3}$ B、4 $\sqrt{3}$ C、8 $\sqrt{3}$ D、4

查看试题解析
7. 如图，在 $△ A B C$ 中， $C D ⊥ A B$ ，垂足为D，E为 $B C$ 边的中点， $A B = 4 ， A C = 2 ， D E = \sqrt{3}$ ，则 $∠ A C D$ （）

A、 $15 °$ B、 $30 °$ C、 $22.5 °$ D、 $45 °$

查看试题解析
8. 赵爽弦图由四个全等的直角三角形所组成，形成一个大正方形，中间是一个小正方形（如图所示）．某次课后服务拓展学习上，小浔绘制了一幅赵爽弦图，她将EG延长交CD于点Ｉ．记小正方形EFGＨ的面积为Ｓ₁ ，大正方形ABCD的面积为Ｓ₂ ，若DＩ＝2，CＩ＝1，Ｓ₂＝5Ｓ₁ ，则GＩ的值是（）

A、 $\frac{\sqrt{10}}{5}$ B、 $\frac{9}{20} \sqrt{2}$ C、 $\frac{\sqrt{5}}{8}$ D、 $\frac{3}{4}$

查看试题解析
9. 如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图，该起重机的变幅索顶端记为点A，变幅索的底端记为点B， $A D$ 垂直地面，垂足为点D， $B C ⊥ A D$ ，垂足为点C．设 $∠ A B C = α$ ，下列关系式正确的是（）

A、 $s i n α = \frac{A B}{B C}$ B、 $s i n α = \frac{B C}{A B}$ C、 $s i n α = \frac{A B}{A C}$ D、 $s i n α = \frac{A C}{A B}$

查看试题解析
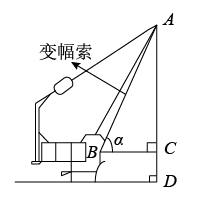10. 如图，线段AB与CD相交于点E，∠AED=45°，DE+AE=9，以AE和CE为边作 $▱$ AGCE，以DE和BE为边作 $▱$ EBFD，且 $▱$ AGCE和 $▱$ EBFD的面积都为3 $\sqrt{2}$ ，若1<CE<3，则线段DF的取值范围是（）

A、 $\frac{3}{4}$ <DF<2 B、 $\frac{6}{7}$ <DF<2 C、 $\frac{6}{7}$ <DF<3 D、1<DF<3

查看试题解析

二、填空题

11. 如图，△ABC的顶点都在正方形网格纸的格点上，则sinC=

查看试题解析
12. 有一块三角形材料如图所示， $∠ A = 30 °$ ， $∠ C = 90 °$ ， $A B = 8$ ．用这块材料剪出一个 $▱ E F D B$ ，其中，点D，E，F分别在 $B C$ ， $A B$ ， $A C$ 上．则剪出的 $▱ E F D B$ 的面积的最大值是．

查看试题解析
13. 如图，在平面直角坐标系 $x O y$ 中， $A B = 2 \sqrt{10}$ ，连结 $A B$ 并延长至C，连结 $O C$ ，若满足 $O C^{2} = B C \cdot A C$ ， $t a n α = 3$ ，则点C的坐标为．

查看试题解析
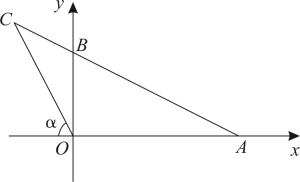14. 如图，在Rt△ABC中，∠ACB=90°，AC<BC，CD平分∠ACB交AB于点D，以DB为直径作⊙O，分别交CD，BC于点E，F，连结BE，EF．则∠EBF=度；若DE=DC， BC=8，则EF的长为

查看试题解析
15. 如图，已知边长为1cm的菱形AFEO，∠AFE＝120°，过点O作两条夹角为60°的射线，分别交边AF，边FE于点M，N，连接MN．则下列命题：
① $S_{四边形 O M F N} = \frac{\sqrt{3}}{4} c m^{2}$ ②MN的长度为定值 ③ $Δ O M N$ 的形状为等边三角形 ④ $\frac{S_{Δ O M N}}{S_{Δ F M N}}$ 的最小值为3，正确的选项有（填序号）

查看试题解析

三、解答题

16. 某型号飞机的机翼形状如图所示，根据图中数据计算 $A B$ 的长度（结果保留小数点后一位， $\sqrt{3} \approx 1.7$ ）.

查看试题解析
17. 如图，已知在Rt△ABC中，∠C=90°，AB=5，BC=3．求AC的长和sinA的值．

查看试题解析
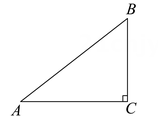18. 如图1是一间安装有壁挂式空调的卧室的一部分，如图2是该空调挂机的侧面示意图.已知空调挂机底部 $B C$ 垂直于墙面 $C D$ ，床 $D E$ 紧靠墙面 $C D$ 放置，当导风板所在的直线 $A E$ 与竖直直线 $A B$ 的夹角 $∠ E A F = 37 °$ 时，空调风刚好吹到床的外边沿E处， $C D ⊥ E D$ 于点D， $A B ⊥ E D$ 于点F.若 $A B = 0.05 m$ ， $B C = 0.2 m$ ，床铺 $E D = 2 m$ ，求空调挂机的底部位置距离床的高度 $C D$ .（参考数据： $s i n 37 ° \approx 0.6$ ， $c o s 37 ° \approx 0.8$ ， $t a n 37 ° \approx 0.75$ ）
图1 图2

查看试题解析

四、综合题

19. 如图，在△ABC中，D是BC边上一点，E是AC边上一点．且满足AD＝AB，∠ADE＝∠C．

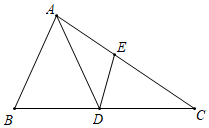(1)、求证：AB²＝AE•AC；

(2)、若D为BC中点，AE＝4，EC＝6，且tanB＝3，求△ABC的面积．

查看试题解析
20. 如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E。CF⊥BD于点F，连接AF，CE。

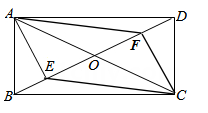(1)、求证：四边形AECF是平行四边形；

(2)、若∠AOB＝60°，AC＝8，求四边形AFCE的面积。

查看试题解析
21. 如图，在菱形ABCD中，AB=5，BD为对角线.点E是边AB延长线上的任意一点，连结DE交BC于点F，BG平分∠CBE交DE于点G．

(1)、求证： $∠ D B G = 90 °$ .

(2)、若 $B D = 6 ， D G = 2 G E$ ．
①求菱形 $A B C D$ 的面积.

②求 $\tan ∠ B D E$ 的值.

(3)、若 $B E = A B$ ，当 $∠ D A B$ 的大小发生变化时（ $0 ° < ∠ D A B < 180 °$ ），在AE上找一点T，使GT为定值，说明理由并求出ET的值．

查看试题解析
22. 如图，在△ABC中，∠ACB为钝角．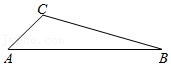

(1)、尺规作图：在边AB上确定一点D，使∠ADC＝2∠B（不写作法，保留作图痕迹，并标明字母）；

(2)、在（1）的条件下，若∠B＝15°，∠ACB＝105°，CD＝3，AC＝ $\sqrt{3}$ ，求△ABC的面积．

查看试题解析
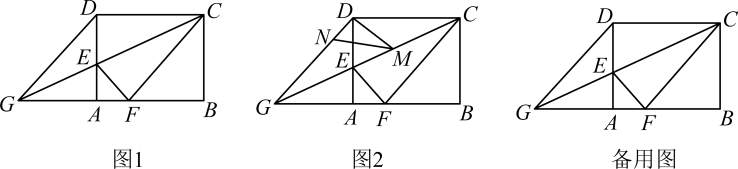23. 如图1，在矩形 $A B C D$ 中， $A B = 10$ ， $A D = 8$ ， $E$ 是 $A D$ 边上的一点，连接 $C E$ ，将矩形 $A B C D$ 沿 $C E$ 折叠，顶点 $D$ 恰好落在 $A B$ 边上的点 $F$ 处，延长 $C E$ 交 $B A$ 的延长线于点 $G$ ．

(1)、求线段 $A E$ 的长；

(2)、求证四边形 $D G F C$ 为菱形；

(3)、如图2， $M$ ， $N$ 分别是线段 $C G$ ， $D G$ 上的动点（与端点不重合），且 $∠ D M N = ∠ D C M$ ，设 $D N = x$ ，是否存在这样的点 $N$ ，使 $△ D M N$ 是直角三角形？若存在，请求出 $x$ 的值；若不存在，请说明理由．

查看试题解析

（苏科版）2022-2023学年九年级数学下册7.5 解直角三角形 同步测试

一、单选题

二、填空题

三、解答题

四、综合题

（苏科版）2022-2023学年九年级数学下册7.5 解直角三角形同步测试