陕西省西安市长安区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-12-14 类型:期末考试
一、单选题
-
1. 下列各组线段中,成比例的一组线段是( )A、2、3、4、5 B、2、3、4、6 C、2、3、4、7 D、2、3、4、82.
如图是一块带有圆形空洞和方形空洞的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的是( )
 A、
A、 B、
B、 C、
C、 D、
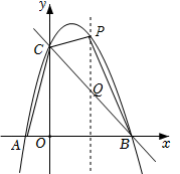
D、 3. a,b是实数,点A(4,a)、B(5,b)在反比例函数y=-的图象上,则( )A、a<b<0 B、b<a<0 C、a<0<b D、b<0<a4. 如图,在5×5的正方形网格中,△ABC的顶点都在格点上,则tan∠BAC的值等于( )
3. a,b是实数,点A(4,a)、B(5,b)在反比例函数y=-的图象上,则( )A、a<b<0 B、b<a<0 C、a<0<b D、b<0<a4. 如图,在5×5的正方形网格中,△ABC的顶点都在格点上,则tan∠BAC的值等于( ) A、 B、3 C、1 D、5. 用配方法解方程时,原方程应变形为( )A、 B、 C、 D、6. 在△ABC中,∠A和∠C都是锐角,且 , , 则△ABC的形状是( )A、直角三角形 B、钝角三角形 C、等边三角形 D、不能确定7. 如图,在△ABC中,AD是∠BAC的平分线,CE与AD交于点M,∠ACE=∠B,下列结论中不正确的是( )
A、 B、3 C、1 D、5. 用配方法解方程时,原方程应变形为( )A、 B、 C、 D、6. 在△ABC中,∠A和∠C都是锐角,且 , , 则△ABC的形状是( )A、直角三角形 B、钝角三角形 C、等边三角形 D、不能确定7. 如图,在△ABC中,AD是∠BAC的平分线,CE与AD交于点M,∠ACE=∠B,下列结论中不正确的是( ) A、△ACM∽△ABD B、△ACE∽△ABC C、△AEM∽△CDM D、△AEM∽△ACD8. 如图,点A在x轴的正半轴上,过线段OA的中点M作MP⊥x轴,交双曲线y=(k>0,x>0)于点P,且OA•MP=10,则k的值为( )
A、△ACM∽△ABD B、△ACE∽△ABC C、△AEM∽△CDM D、△AEM∽△ACD8. 如图,点A在x轴的正半轴上,过线段OA的中点M作MP⊥x轴,交双曲线y=(k>0,x>0)于点P,且OA•MP=10,则k的值为( ) A、-5 B、5 C、20 D、109. 如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED的度数为( )
A、-5 B、5 C、20 D、109. 如图,菱形ABCD中,AC交BD于O,DE⊥BC于E,连接OE,若∠ABC=140°,则∠OED的度数为( ) A、15° B、20° C、25° D、30°10. 抛物线y=ax2+bx+c的图象经过原点和第一、二、三象限,那么下列结论成立的是( )A、a>0,b>0,c=0 B、a>0,b<0,c=0 C、a<0,b>0,c=0 D、a<0,b<0,c=0
A、15° B、20° C、25° D、30°10. 抛物线y=ax2+bx+c的图象经过原点和第一、二、三象限,那么下列结论成立的是( )A、a>0,b>0,c=0 B、a>0,b<0,c=0 C、a<0,b>0,c=0 D、a<0,b<0,c=0二、填空题
-
11. 反比例函数的图象位于第一、三象限,其中第一象限内的图象经过点 , 请在第三象限内的图象上找一个你喜欢的点 , 你选择的点坐标为.12. 在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同.摇匀后从中摸出一个球,记下颜色后再放回袋中.不断重复这一过程,共摸球100次.其中有40次摸到黑球,估计袋中红球的个数是 .13. 如图,△ABC中,点D在边AB上,满足∠ADC=∠ACB,若AC=2,AD=1,则DB= .
 14. 抛物线的图象如图所示,若将其向左平移2个单位,再向下平移3个单位,则平移后的解析式为.
14. 抛物线的图象如图所示,若将其向左平移2个单位,再向下平移3个单位,则平移后的解析式为.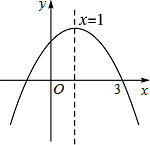 15. 如图,正方形ABCD和正方形EFCG的边长分别为6和2,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为.
15. 如图,正方形ABCD和正方形EFCG的边长分别为6和2,点F,G分别在边BC,CD上,P为AE的中点,连接PG,则PG的长为.
三、解答题
-
16. 计算:17. 解方程:18. 已知 , , 求的值.19. 如图,AB、CD两根木杆竖直地立在地面上,课间小明观察到木杆AB在地面上的影子为BE,B、E、D在一条直线上,请用尺规作出木杆CD此时在地面上的影子DP.
 20. 如图,已知一次函数(b为常数)的图象与反比例函数(k为常数)的图象相交于A、B两点,已知点A的坐标为(1,4).
20. 如图,已知一次函数(b为常数)的图象与反比例函数(k为常数)的图象相交于A、B两点,已知点A的坐标为(1,4). (1)、求一次函数与反比例函数的表达式;(2)、求点B的坐标,并根据图象直接写出满足的自变量x的取值范围.21. 一天小明与父亲爬山,在停车场附近看到了一棵树,小明想测量这棵树的高度,他发现树的影子恰好落在地面和一斜坡上(如图所示),此时测得地面上的影长为12米,坡面上的影长为5米、斜坡的坡角为30°,同一时刻,一根长为1米垂直于地面放置的拐杖在地面上的影长为2.5米,求这棵树的高度(结果精确到0.1米).
(1)、求一次函数与反比例函数的表达式;(2)、求点B的坐标,并根据图象直接写出满足的自变量x的取值范围.21. 一天小明与父亲爬山,在停车场附近看到了一棵树,小明想测量这棵树的高度,他发现树的影子恰好落在地面和一斜坡上(如图所示),此时测得地面上的影长为12米,坡面上的影长为5米、斜坡的坡角为30°,同一时刻,一根长为1米垂直于地面放置的拐杖在地面上的影长为2.5米,求这棵树的高度(结果精确到0.1米). 22. 有两部大小一样但型号不同的手机A、B,现有6个手机壳,其中与手机A匹配的手机壳有2个,与手机B匹配的手机壳有3个,还有1个手机壳与两部手机都不匹配.(1)、从6个手机壳中随机的取一个,求恰好与手机A匹配的概率;(2)、随机取一部手机和一个手机壳,求恰好能匹配的概率(用树状图或列表法解答).23. 如图,在正方形ABCD中,点P是BC延长线上一点,连接AP,过点B作BE⊥AP于点E,过点D作DF⊥AP于点F.
22. 有两部大小一样但型号不同的手机A、B,现有6个手机壳,其中与手机A匹配的手机壳有2个,与手机B匹配的手机壳有3个,还有1个手机壳与两部手机都不匹配.(1)、从6个手机壳中随机的取一个,求恰好与手机A匹配的概率;(2)、随机取一部手机和一个手机壳,求恰好能匹配的概率(用树状图或列表法解答).23. 如图,在正方形ABCD中,点P是BC延长线上一点,连接AP,过点B作BE⊥AP于点E,过点D作DF⊥AP于点F. (1)、证明:△ABE≌△DAF;(2)、若AB=10,∠P=30°,求EF的长.24. 为了满足初中学业水平体育与健康考试的需求,某体育用品专卖店从厂家以单价40元进购了一种排球,如果以单价60元出售,那么每月可售出400个,根据销售经验,销售单价每提高1元,销售量相应减少5个.(1)、设销售单价提高x元,则每个排球获得的利润是元;这种排球这个月的销售量是个;(2)、若该专卖店准备在这种排球销售上一月获利10500元,同时又要使顾客得到实惠,则售价应定为多少元?
(1)、证明:△ABE≌△DAF;(2)、若AB=10,∠P=30°,求EF的长.24. 为了满足初中学业水平体育与健康考试的需求,某体育用品专卖店从厂家以单价40元进购了一种排球,如果以单价60元出售,那么每月可售出400个,根据销售经验,销售单价每提高1元,销售量相应减少5个.(1)、设销售单价提高x元,则每个排球获得的利润是元;这种排球这个月的销售量是个;(2)、若该专卖店准备在这种排球销售上一月获利10500元,同时又要使顾客得到实惠,则售价应定为多少元?