陕西省西安市长安区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-12-14 类型：期末考试

进入出卷网下载

一、单选题

1. 比 $\sqrt{2}$ 大的数是（）

A、1 B、2 C、0 D、-2

查看试题解析
2. 下列各组数中，不是勾股数组的是（）

A、5，12，13 B、6，8，10 C、7，8，9 D、3，4，5

查看试题解析
3. 函数 y=2x-1的图象不经过的点是（　　）

A、（1，1） B、（2，3） C、（﹣1，﹣1） D、（﹣2，﹣5）

查看试题解析
4. 已知一次函数y=2x+n的图像如图所示，则方程2x+n=0的解可能是（）

A、x=1 B、x= $\frac{3}{2}$ C、x=- $\frac{3}{5}$ D、x=-1

查看试题解析
5. 用加减法解方程组 ${\begin{array}{l} x + y = - 3 ① \\ 3 x + y = 6 ② \end{array}$ 由②-①消去未知数 $y$ ，所得到的一元一次方程是（）

A、 $2 x = 9$ B、 $2 x = 3$ C、 $4 x = 9$ D、 $4 x = 3$

查看试题解析
6. 2021年是中国共产党建党100周年，某校开展“敬建党百年，承红色基因”读书活动.为了了解某班开展学习党史情况，该校随机抽取了9名学生进行调查，他们读书的本数分别是3、2、3、2、5、1、2、5、4，则这组数据的众数和中位数分别是（）

A、2和3 B、2和5 C、5和3 D、3和5

查看试题解析
7. 如图所示，下列条件中，不能推出AB∥CE成立的条件是（）

A、∠A＝∠ACE B、∠B＝∠ACE C、∠B＝∠ECD D、∠B+∠BCE＝180°

查看试题解析
8. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏，如图，是一局象棋残局，若表示棋子“炮”和“車”的点的坐标分别为（1，2），（-2，0），则表示棋子“馬”的点的坐标为（）

A、（-3，3） B、（-3，2） C、（4，2） D、（3，2）

查看试题解析
9. 如图，函数 $y = a x + b$ 和 $y = k x$ 的图象交于点P，则根据图象可得，关于x、y的二元一次方程组 ${\begin{array}{l} a x - y + b = 0 \\ k x - y = 0 \end{array}$ 的解是（）．

A、 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ B、 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = - 3 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$

查看试题解析
10. 如图，直线 $A B ∥ C D$ ，点E、F分别是AB、CD上的点（点E在点F的右侧），点M为线段EF上的一点（点M不与点E、F重合），点N为射线FD上的一动点，连接MN，过点M作 $M Q ∥ C D$ ，且恰能使得MQ平分∠EMN.若 $∠ B E F = 142 °$ ，则∠MNF和∠FMN的度数分别为（）

A、38°，76° B、38°，104° C、36°，142° D、36°，104°

查看试题解析

二、填空题

11. 计算： $\sqrt{4} + (- \sqrt{2})^{2} =$ .

查看试题解析
12. 把命题“互为相反数的两个数的和为零”写成“如果…那么…”的形式：.

查看试题解析
13. 如图，若∠1与∠2互补，∠3与∠2互补，则 $∠ 1 = ∠ 3$ ，用一个定理表达你所得到的结论.

查看试题解析
14. 某招聘考试分笔试和面试两项，笔试成绩和面试成绩按3：2计算平均成绩.若小明笔试成绩为85分，面试成绩为90分，则他的平均成绩是分.

查看试题解析
15. 已知关于x，y的二元一次方程3mx-y=-1有一组解是 ${\begin{matrix} x = 1 \\ y = - 2 \end{matrix}$ ，则m的值是 .

查看试题解析
16. 已知，一次函数 $y = k x + b$ 的图象不经过第三象限，且点 $(1 ， y_{1})$ ， $(- 1 ， y_{2})$ 在该函数图象上，则 $y_{1} - y_{2}$ 0（用“＞、＜、＝”连接）

查看试题解析
17. 《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1，图2所示，图中各行从左到右列出的算筹数分别表示未知数 $x ， y$ 的系数与相应的常数项．把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来，就是 ${\begin{array}{l} 3 x + 2 y = 19 \\ x + 4 y = 23 \end{array}$ ．类似地，图2所示的算筹图我们可以表述为．

查看试题解析
18. 如图，直线a过正方形ABCD的顶点A ，点B、D到直线a的距离分别为5、12，则正方形的周长为．

查看试题解析

三、解答题

19. 解方程组： ${\begin{matrix} 2 x - y = 5 \\ 3 x + 4 y = 2 \end{matrix}$

查看试题解析
20. 如图，在△ABC中，∠BAC=90°，AB=AC=a，AD是△ABC的高，求AD的长.

查看试题解析
21. 下列表格是刘小明一学期数学成绩的记录，根据表格提供的信息回答下面的问题：（注：每次考试满分都是100分）
考试类别
平时成绩
期中考试
期末考试
第四章
第五章
第六章
第七章
成绩
88
92
90
86
90
96
注：可能用到的公式. $s^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + ⋯ ⋯ + {(x_{n} - \bar{x})}^{2}]$

(1)、刘小明6次成绩的众数与中位数之差是；

(2)、计算刘小明平时成绩的平均分；

(3)、计算刘小明平时成绩的方差；

(4)、按照学校规定，本学期的综合成绩的权重如扇形图所示，请你求出刘小明本学期的综合成绩，要写出解题过程.

查看试题解析
22. 某中学计划举行以“奋斗百年路，启航新征程”为主题的知识竞赛，并对获奖的同学给予奖励.现要购买甲、乙两种奖品，已知1件甲种奖品和2件乙种奖品共需40元，2件甲种奖品和3件乙种奖品共需70元.

(1)、求甲、乙两种奖品的单价；

(2)、根据颁奖计划，该中学需甲、乙两种奖品共60件，且甲种奖品不少于20件，应如何购买才能使总费用最少？并求出最少费用.

查看试题解析
23. 在如图直角坐标系中：

(1)、画出y＝-2x+6函数的图象；

(2)、分别写出函数y＝-2x+6与x轴、y轴的交点A、B的坐标；

(3)、在x轴上有一点C，且△ABC的面积为12，求点C的坐标.

查看试题解析
24. 在综合与实践课上，同学们以“一个含30°的直角三角尺和两条平行线”为背景开展数学活动如图1，已知两直线a，b，且 $a ∥ b$ 和直角三角形ABC， $∠ B C A = 90 °$ ， $∠ B A C = 30 °$ .

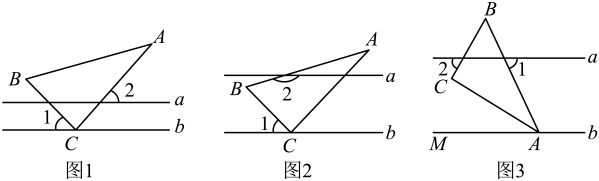(1)、在图1中，∠1＝46°，求∠2的度数；

(2)、如图2，创新小组的同学把直线a向上平移，并把∠2的位置改变，发现 $∠ 2 - ∠ 1 = 120 °$ ，说明理由；

(3)、竞赛小组在创新小组发现结论的基础上，将图2中的图形继续变化得到图3，当AC平分∠BAM时，此时发现∠1与∠2又存在新的数量关系，请写出∠1与∠2的数量关系并证明.

查看试题解析

考试类别	平时成绩				期中考试	期末考试
考试类别	第四章	第五章	第六章	第七章	期中考试	期末考试
成绩	88	92	90	86	90	96