陕西省西安市莲湖区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-12-14 类型:期末考试
一、单选题
-
1. 9的算术平方根是( )A、 ﹣3 B、±3 C、3 D、2. 2021年6月17日神舟十二号飞船于在甘肃酒泉发射升空,在太空驻留90天后于9月14日返回地球,下列描述能确定飞船着陆位置的是( )A、内蒙古中部 B、酒泉卫星发射中心东南方向处 C、东经 D、北纬3. 点和点在正比例函数的图象上,当时,则与的大小关系是( )A、 B、 C、 D、无法判断4. 准备在甲,乙,丙,丁四人中选取成绩稳定的一名参加射击比赛,在相同条件下每人射击10次,已知他们的平均成绩相同,方差分别是 , , , , 则应该选择哪位运动员参赛( )A、丁 B、丙 C、乙 D、甲5. 一次函数y=x﹣1的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 已知△ABC的三个内角分别为∠A、∠B、∠C,三边分别为a、b、c,下列条件不能判定△ABC是直角三角形的是( )A、∠A:∠B:∠C=3:4:7 B、∠A=∠B﹣∠C C、a:b:c=2:3:4 D、b2=(a+c)(a﹣c)7. 如图,在中,点D,E,F分别在边 , , 上,下列不能判定的条件是( )
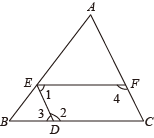 A、 B、 C、 D、8. 一个两位数,十位数字比个位数字大4;将这个两位数的十位数字与个位数字对调后,比原数减少了36,求原两位数.若设原两位数十位数字是x,个位数字是y,则列出方程组为( )A、 B、 C、 D、
A、 B、 C、 D、8. 一个两位数,十位数字比个位数字大4;将这个两位数的十位数字与个位数字对调后,比原数减少了36,求原两位数.若设原两位数十位数字是x,个位数字是y,则列出方程组为( )A、 B、 C、 D、二、填空题
-
9. 比较大小:.(填:“>”、“<”或“=”)10. 已知中, , , 则的度数为.11. 某博物馆拟招聘一名优秀讲解员,其中小林笔试、试讲、面试三轮测试得分分别为92分,80分、85分.综合成绩中笔试占50%、试讲占30%、面试占20%,那么小林的最后得分为分.12. 如图,把一块等腰直角三角尺和直尺按此位置放置,如果 , 则的度数为.
 13. 在平面直角坐标系内,若两条直线和的交点在第三象限的角平分线上,则b的值为.
13. 在平面直角坐标系内,若两条直线和的交点在第三象限的角平分线上,则b的值为.三、解答题
-
14. 计算:.15. 计算:.16. 解方程组: .17. 尺规作图,如图过点A作直线l的平行线(不写作法,保留作图痕迹).
 18. 如图, , 点G在上,B,C,G三点在同一条直线上,且 , .求证:.
18. 如图, , 点G在上,B,C,G三点在同一条直线上,且 , .求证:. 19. 如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?
19. 如图,一高层住宅发生火灾,消防车立即赶到距大厦12米(的长)处,升起云梯到火灾窗口,云梯长20米,云梯底部距地面3米(的长),问:发生火灾的住户窗口距离地面有多高(的长)?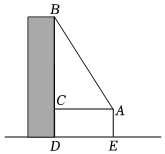 20. 已知 , 与x成正比例,与成正比例,当时,;当时, , 求y与x之间的函数关系式.21. 如图,在平面直角坐标系中, , , .
20. 已知 , 与x成正比例,与成正比例,当时,;当时, , 求y与x之间的函数关系式.21. 如图,在平面直角坐标系中, , , .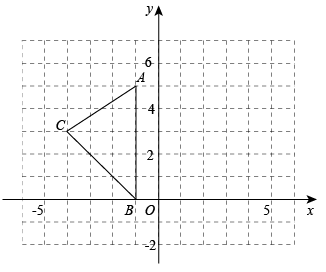 (1)、在图中作出关于y轴的对称图形.(2)、写出点和的坐标.22. 健康的体魄是青少年为祖国和人民服务的基本前提,是中华民族旺盛生命力的体现.某初中学校为了提高学生体质健康,制定合理的校园阳光体育锻炼方案,随机抽查了部分学生最近两周参加体育锻炼活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:
(1)、在图中作出关于y轴的对称图形.(2)、写出点和的坐标.22. 健康的体魄是青少年为祖国和人民服务的基本前提,是中华民族旺盛生命力的体现.某初中学校为了提高学生体质健康,制定合理的校园阳光体育锻炼方案,随机抽查了部分学生最近两周参加体育锻炼活动的天数,并用得到的数据绘制了两幅统计图,下面给出了两幅不完整的统计图:
请根据图中提供的信息,回答下列问题:
(1)、补全条形统计图.(2)、本次抽样调查的众数为 , 中位数为 .(3)、如果该校约有3500名学生,请你估计全校约有多少名学生参加体育锻炼的天数不少于7天?23. 某年级为了奖励知识竞赛的优胜者,年级组派李老师去超市买钢笔和笔记本作为奖品.该超市某品牌的笔记本每本a元,钢笔每支b元.若购买4本笔记本和2支钢笔,需70元;若购买3本笔记本和1支钢笔,则需45元.求a,b的值.24. 观察下列各式:;;.(1)、请根据以上规律,写出第4个式子:.(2)、请根据以上规律,写出第n个式子():.(3)、根据以上规律计算:的值.25. 甲、乙两地相距 , 一辆货车和一辆轿车先后从甲地匀速开往乙地,轿车晚出发.货车和轿车各自与甲地的距离y(单位:)与货车行驶的时间x(单位:h)之间的关系如图所示. (1)、分别求出轿车行驶过程中 , 货车行驶过程中关于x的函数表达式,并写出自变量x的取值范围.(2)、货车与轿车在货车出发多长时间后相遇.26. 已知, , 直线与直线 , 分别交于点E,F.
(1)、分别求出轿车行驶过程中 , 货车行驶过程中关于x的函数表达式,并写出自变量x的取值范围.(2)、货车与轿车在货车出发多长时间后相遇.26. 已知, , 直线与直线 , 分别交于点E,F. (1)、如图1,若 , 求的度数.(2)、如图2,与的角平分线交于点P,与交于点G,H是上一点,且.求证:.(3)、如图3,在(2)的条件下,连接 , K是上一点使 , 作平分 , 问的大小是否发生变化?若不变,请求出其值;若变化,说明理由.
(1)、如图1,若 , 求的度数.(2)、如图2,与的角平分线交于点P,与交于点G,H是上一点,且.求证:.(3)、如图3,在(2)的条件下,连接 , K是上一点使 , 作平分 , 问的大小是否发生变化?若不变,请求出其值;若变化,说明理由.