江苏省盐城市地区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-12-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，是关于x的一元二次方程的是（）

A、 $x + \frac{1}{x} = 2$ B、2x²﹣x＝1 C、3x³＝1 D、xy＝4

查看试题解析
2. 设方程 $x^{2} - 3 x + 2 = 0$ 的两根分别是 $x_{1} ， x_{2}$ ，则 $x_{1} + x_{2}$ 的值为（）

A、3 B、 $- \frac{3}{2}$ C、 $\frac{3}{2}$ D、-2

查看试题解析
3. 如图，ABCD为圆内接四边形，若∠A＝60°，则∠C等于（）

A、30° B、60° C、120° D、300°

查看试题解析
4. 已知 $⊙ O$ 的半径是4，点P到圆心O的距离为5，则点P在（）

A、 $⊙ O$ 的内部 B、 $⊙ O$ 的外部 C、 $⊙ O$ 上或 $⊙ O$ 的内部 D、 $⊙ O$ 上或 $⊙ O$ 的外部

查看试题解析
5. 从拼音“shuxue”中随机抽取一个字母，抽中字母u的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析
6. 一组数据x、0、1、－2、3的平均数是1，则x的值是（）

A、3 B、1 C、2.5 D、0

查看试题解析
7. 将抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 向下平移两个单位，以下说法错误的是（）

A、开口方向不变 B、对称轴不变 C、y随x的变化情况不变 D、与y轴的交点不变

查看试题解析
8. 表中列出的是一个二次函数的自变量x与函数y的几组对应值：
x
…
－2
0
1
3
…
y
…
6
－4
－6
－4
…
下列各选项中，正确的是（）

A、这个函数的最小值为－6 B、这个函数的图象开口向下 C、这个函数的图象与x轴无交点 D、当 $x > 2$ 时，y的值随x值的增大而增大

查看试题解析

二、填空题

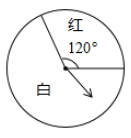
9. 抛物线 $y = - 2 {(x + 2)}^{2} - 5$ 的顶点坐标是.

查看试题解析
10. 方程x²﹣x=0的解是．

查看试题解析
11. 一组数据分别为：79、81、77、82、75、82，则这组数据的中位数是.

查看试题解析
12. 已知圆锥的底面圆半径为4，母线长为5，则圆锥的侧面积是.

查看试题解析
13. 二次函数 $y = (x - 1) (x - a)$ （a为常数）的图象的对称轴为直线 $x = 2$ .则 $a =$ .

查看试题解析
14. 转动如图所示的转盘，当转盘停止时，指针落在红色区域的概率是.

查看试题解析
15. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则三个代数式①abc，② $b^{2} - 4 a c$ ， ③ $a - b + c$ 中，值为正数的有.（填序号）

查看试题解析
16. 如图中的三个图形都是边长为1的小正方形组成的网格，其中第一个图形有 $1 \times 1$ 个正方形，所有线段的和为4，第二个图形有 $2 \times 2$ 个小正方形，所有线段的和为12，第三个图形有 $3 \times 3$ 个小正方形，所有线段的和为24，按此规律，则第n个网格所有线段的和为.(用含n的代数式表示)

查看试题解析

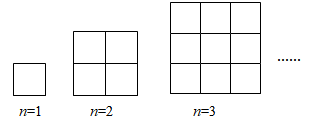
三、解答题

17. 解方程

(1)、 ${(x - 1)}^{2} - 9 = 0$

(2)、 $x^{2} - 2 x - 5 = 0$

查看试题解析
18. 已知关于x的一元二次方程x²+x−m=0.

(1)、设方程的两根分别是x₁ ， x₂ ，若满足x₁+x₂=x₁•x₂ ，求m的值.

(2)、二次函数y=x²+x−m的部分图象如图所示，求m的值.

查看试题解析
19. 已知二次函数 $y = x^{2} - 4 x + 3$ .

(1)、将 $y = x^{2} - 4 x + 3$ 化成 $y = a {(x - h)}^{2} + k$ 的形式：；

(2)、这个二次函数图象与x轴交点坐标为；

(3)、这个二次函数图象的最低点的坐标为；

(4)、当 $y < 0$ 时，x的取值范围是.

查看试题解析
20. 已知关于x的一元二次方程： $x^{2} - (2 k + 2) x + k^{2} + 2 k = 0$ .

(1)、当 $k = 2$ 时，求方程的根；

(2)、求证：这个方程总有两个不相等的实数根.

查看试题解析
21. 九年级某班要召开一次“走近抗疫英雄，讲好中国故事”主题班会活动，李老师制作了编号为A、B、C、D的4张卡片（如图，除编号和内容外，其余完全相同），并将它们背面朝上洗匀后放在桌面上．

(1)、小明随机抽取1张卡片，抽到卡片编号为B的概率为；

(2)、小明从4张卡片中随机抽取1张（不放回），小丽再从余下的3张卡片中随机抽取1张，然后根据抽取的卡片讲述相关英雄的故事，求小明、小丽两人中恰好有一人讲述钟南山抗疫故事的概率（请用“画树状图”或“列表”等方法写出分析过程）．

查看试题解析
22. 某学校从九年级同学中任意选取40人，随机分成甲、乙两个小组进行“引体向上”体能测试，每组20人，根据测试成绩绘制出统计表和如图所示的统计图（成绩均为整数，满分为10分）
甲组成绩统计表：
成绩
7
8
9
10
人数
1
9
5
5
根据上面的信息，解答下列问题：

(1)、甲组的平均成绩为分，甲组成绩的中位数是，
乙组成绩统计图中 $m =$ ，乙组成绩的众数是；

(2)、根据图表信息，请你判断哪个小组的成绩更加稳定？只需要直接写出结论.

查看试题解析
23. 如图，AB、AC分别是半 $⊙ O$ 的直径和弦， $O D ⊥ A C$ 于点D，过点A作半 $⊙ O$ 的切线AP，AP与OD的延长线交于点P，连接PC并延长与AB的延长线交于点F.

(1)、求证：PC是半 $⊙ O$ 的切线；

(2)、若 $∠ C A B = 30 °$ ， $A B = 6$ ，求由劣弧AC、线段AC所围成图形的面积S.

查看试题解析
24. 【概念提出】圆心到弦的距离叫做该弦的弦心距．
【数学理解】如图①，在 $⊙ O$ 中，AB是弦， $O P ⊥ A B$ ，垂足为P，则OP的长是弦AB的弦心距．

(1)、若 $⊙ O$ 的半径为5，OP的长为3，则AB的长为．

(2)、若 $⊙ O$ 的半径确定，下列关于AB的长随着OP的长的变化而变化的结论：
①AB的长随着OP的长的增大而增大；②AB的长随着OP的长的增大而减小；③AB的长与OP的长无关．
其中所有正确结论的序号是．

(3)、【问题解决】若弦心距等于该弦长的一半，则这条弦所对的圆心角的度数为°．

(4)、已知如图②给定的线段EF和 $⊙ O$ ，点Q是 $⊙ O$ 内一定点．过点Q作弦AB，满足 $A B = E F$ ，请问这样的弦可以作条．

查看试题解析
25. 某水果超市经销一种高档水果，进价每千克40元.

(1)、若按售价为每千克50元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，超市决定采取适当的涨价措施，但超市规定每千克涨价不能超过8元，若每千克涨价1元，日销售量将减少20千克.现该超市希望每天盈利6000元，那么每千克应涨价多少元？

(2)、在（1）的基础上，利用函数关系式求出每千克水果涨价多少元时，超市每天可获得最大利润？最大利润是多少？

查看试题解析
26. 如图，点P在y轴的正半轴上， $⊙ P$ 交x轴于B、C两点，以AC为直角边作等腰Rt△ACD，BD分别交y轴和 $⊙ P$ 于E、F两点，连接AC、FC，AC与BD相交于点G.

(1)、求证： $∠ A C F = ∠ A D B$ ；

(2)、求证： $C F = D F$ ；

(3)、 $∠ D B C =$ °；

(4)、若 $O B = 3$ ， $O A = 6$ ，则△GDC的面积为.

查看试题解析
27. 如图1，在平面直角坐标系中，直线y=-6x+6与x轴、y轴分别交于A、C两点，抛物线y=x²+bx+c经过A、C两点，与x轴的另一交点为B.

(1)、抛物线解析式为；

(2)、若点M为x轴下方抛物线上一动点，MN⊥x轴交BC于点N，当点M运动到某一位置时，线段MN的长度最大，求此时点M的坐标及线段MN的长度；

(3)、如图2，以B为圆心、2为半径的⊙B与x轴交于E、F两点（F在E右侧），若点P是⊙B上一动点，连接PA，以PA为腰作等腰Rt△PAD，使∠PAD=90°（P、A、D三点为逆时针顺序），连接FD.
①将线段AB绕点A顺时针旋转90°，请直接写出B点的对应点B′的坐标；
②求FD长度的取值范围.

查看试题解析

x	…	－2	0	1	3	…
y	…	6	－4	－6	－4	…

成绩	7	8	9	10
人数	1	9	5	5