江苏省宿迁市沭阳县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-12-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下列关于 $x$ 的方程中，一定是一元二次方程的是（）

A、 $a x^{2} + b x + c = 0$ B、 $(x + 2) (x - 3) = (x - 1 {)^{2}}^{}$ C、 $x^{2} + 1 = 0$ D、 $\frac{1}{x} + x = 1$

查看试题解析
2. 已知一组数据2，3，5，x，5，3有唯一的众数3，则x的值是（）

A、3 B、5 C、2 D、无法确定

查看试题解析
3. 若一元二次方程 $a x^{2} + 2 x + 1 = 0$ 有两个不相等的实数根，则实数a的取值范围是（）

A、 $a < 1$ B、 $a \leq 1$ C、 $a \leq 1$ 且 $a \neq 0$ D、 $a < 1$ 且 $a \neq 0$

查看试题解析
4. ⊙O的直径为10cm，点A到圆心O的距离OA=6cm，则点A与⊙O的位置关系为（）

A、点A在圆上 B、点A在圆外 C、点A在圆内 D、无法确定

查看试题解析
5. 二次函数 $y = x^{2} - 2 x$ 的顶点坐标是（）

A、 $(2 ， - 4)$ B、 $(2 ， 4)$ C、 $(1 ， - 1)$ D、 $(1 ， 1)$

查看试题解析
6. 将半径为16cm的半圆形纸片围成一个圆锥的侧面，则这个圆锥的底面半径是（）

A、4cm B、6cm C、8cm D、10cm

查看试题解析
7. 如图，在 $▱ A B C D$ 中，E为 $B C$ 边上的点，若 $B E ： E C = 2 ： 3$ ， $A E$ 交 $B D$ 于F，则 $B F ： F D$ 等于（）

A、4：5 B、2：5 C、5：9 D、4：9

查看试题解析
8. 抛物线 $y = x^{2} + b x + 3$ 的对称轴为直线 $x = 1$ .若关于x的一元二次方程 $x^{2} + b x + 3 - t = 0$ （t为实数）在 $- 1 < x < 3$ 的范围内有实数根，则t的取值范围是（）

A、 $2 \leq t < 11$ B、 $t \geq 2$ C、 $6 < t < 11$ D、 $2 \leq t < 6$

查看试题解析

二、填空题

9. 四边形 $A B C D$ 内接于⊙ $O$ ，若 $∠ B = 85 °$ ，则 $∠ D =$ $°$ .

查看试题解析
10. 已知 $\frac{x}{2} = \frac{y}{3} = \frac{z}{4}$ ，则 $\frac{x + y}{z} =$ .

查看试题解析
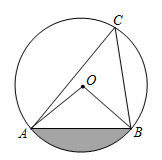
11. 已知点 $A (0 ， a) ， B (4 ， b)$ 是抛物线 $y = x^{2} - 2 x + 2022$ 上的两点，则a，b的大小关系是.

查看试题解析
12. 甲、乙、丙、丁四人参加射击比赛，经过三轮的初赛，他们成绩的方差分别是 ${s^{2}}_{甲} = 0.2 ， {s^{2}}_{乙} = 0.3 ， {s^{2}}_{丙} = 0.25 ， {s^{2}}_{丁} = 0.4$ ，你认为成绩更稳定的是.

查看试题解析
13. 已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 4 x + 3 = 0$ 的两根，则 $x_{1} + x_{2} - 2 x_{1} x_{2} =$ .

查看试题解析
14. 2022年的春节即将到来，一年一度的“春节联欢晚会”即将拉开序幕，若“春节联欢晚会”的舞台纵深10米，若想获得最佳的音响效朵，主持人应该站在舞台纵深所作线离舞台前沿较近的黄金分割点P处，那么主持人站立的位置离舞台前沿较近的距离为.（结果保留根号）

查看试题解析
15. 已知圆心角为 $135 °$ 的扇形面积为 $24 π$ ，则扇形的半径为.

查看试题解析
16. 如图，在 $⊙ O$ 中， $O A = 3$ ， $∠ C = 45 °$ ，则图中阴影部分的面积是.（结果保留 $π$ ）

查看试题解析
17. 在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，现给出以下结论：① $a b c < 0$ ；② $c + 2 a < 0$ ；③ $9 a - 3 b + c = 0$ ；④ $a - b \geq m (a m + b)$ （m为实数），其中正确的结论有.（只填序号）

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， A C = 8 ， B C = 6$ ，点P是平面内一个动点，且 $A P = 4$ ， Q为 $B P$ 的中点，在P点运动过程中，设线段 $C Q$ 的长度为m，则m的取值范围是.

查看试题解析

三、解答题

19. 计算：

(1)、 $x^{2} - 2 x - 3 = 0$

(2)、先化简，再求值： $(\frac{a^{2} - 4}{a^{2} - 4 a + 4} - \frac{1}{2 - a}) \div \frac{2}{a^{2} - 2 a}$ ，其中a满足 $a^{2} + 3 a - 3 = 0$ .

查看试题解析
20. 关于x的一元二次方程x²-（k+1）x+2k-2＝0.

(1)、求证：方程总有两个实数根；

(2)、若方程有一根小于2，求k的取值范围.

查看试题解析
21. 如图所示，在网格中，每个小正方形的边长均为1个单位长度，把小正方形的顶点叫做格点，O为平面直角坐标系的原点，矩形OABC的4个顶点均作格点上，连接对角线OB.
⑴在平面直角坐标系内，以原点O为位似中心，把△OAB缩小，作出它的位似图形，并且使所作的位似图形与△OAB的相似比等于 $\frac{1}{2}$ ；
⑵将△OAB以O为旋转中心，逆时针旋转90°，得到△OA₁B₁ ，作出△OA₁B₁ ，并求出线段OB旋转过程中所形成扇形的面积.

查看试题解析
22. 将4张印有“梅”“兰”“竹”“菊”字样的卡片（卡片的形状、大小、质地都相同）放在一个不透明的盒子中，将卡片搅匀.

(1)、从盒子中任意取出1张卡片，恰好取出印有“兰”字的卡片的概率为.

(2)、先从盒子中任意取出1张卡片，记录后放回并搅匀，再从中任意取出1张卡片，求取出的两张卡片中，至少有1张印有“兰”字的概率（请用画树状图或列表等方法求解）.

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A E$ 平分 $∠ B A C$ 交 $B C$ 于点E，点D在 $A B$ 上， $D E ⊥ A E$ .⊙ $O$ 是 $R t △ A D E$ 的外接圆，交 $A C$ 于点F.

(1)、求证： $B C$ 是⊙ $O$ 的切线；

(2)、若⊙ $O$ 的半径为10， $A C = 16$ ，求 $S_{△ A D E}$ .

查看试题解析
24. 某校利用课外活动时间，开设了书法、健美操、兵兵球和朗诵四个社团活动，每个学生选择一项活动参加，为了了解活动开展情况，学校随机抽取了部分学生进行调查，将调查结果绘制成如下不完整的条形统计图和扇形统计图.

(1)、请直接填写抽取的学生有人， $n =$ ， $a =$ .

(2)、补全条形统计图；

(3)、若该校有学生4000人，估计参加书法社团活动的学生人数.

查看试题解析
25. 如图，河对岸有一路灯杆 $A B$ ，在灯光下，小明在点D处，自己的影长 $D F = 4 m$ ，沿 $B D$ 方向到达点F处再测自己的影长 $F G = 5 m$ ，如果小明的身高为 $1.6 m$ ，求路灯杆 $A B$ 的高度.

查看试题解析
26. 2020年是脱贫攻坚的收官之年，老李在驻村干部的帮助下，利用网络平台进行“直播带货”，销售一批成本为每件30元的商品，按单价不低于成本价，且不高于50元销售，经调查发现，该商品每天的销售量y（件）与销售单价x（元）之间满足一次函数关系，部分数据如表所示.

销售单价x（元）

30

40

45

销售数量y（件）

100

80

70

(1)、求该商品每天的销售量y（件）与销售单价x（元）之间的函数关系式；

(2)、销售单价定为多少元时，每天的销售利润为800元？

(3)、销售单价定为多少元时，才能使销售该商品每天获得的利润w（元）最大？最大利润是多少元？

查看试题解析
27. 如图①， $△ A B C$ 和 $△ A D E$ 是有公共顶点的等腰直角三角形， $∠ B A C = ∠ D A E = 90 °$ ，点P为射线 $B D ， C E$ 的交点.

(1)、如图②，将 $△ A D E$ 绕点A旋转，当C、D、E在同一条直线上时，连接 $B D$ 、 $B E$ ，求证： $B D = C E$ 且 $B D ⊥ C E$ .

(2)、若 $A B = 8 ， A D = 4$ ，把 $△ A D E$ 绕点A旋转，
①当 $∠ E A C = 90 °$ 时，求 $P B$ 的长；

②旋转过程中线段 $B P$ 长的最小值是 ▲ .

查看试题解析
28. 如图，在平面直角坐标系内，抛物线 $y = a x^{2} + b x - 8 (a \neq 0)$ 与x轴交于点A、点B，与y轴交于点C，且 $O B = 2 O A$ .过点A的直线 $y = x + 4$ 与抛物线交于点E.点P为第四象限内抛物线上的一个动点，过点P作 $P H ⊥ A E$ 于点H.

(1)、抛物线的表达式中， $a =$ ， $b =$ ；

(2)、在点P的运动过程中，若 $P H$ 取得最大值，求这个最大值和点P的坐标；

(3)、在（2）的条件下，在x轴上求点Q，使以A，P，Q为顶点的三角形与 $△ A B E$ 相似.

查看试题解析

销售单价x（元）	30	40	45
销售数量y（件）	100	80	70