江苏省淮安市涟水县2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-12-14 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 下列图形中，既是中心对称图形，又是轴对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 方程x2=1的根是（　　）


    A、x=1  B、x=﹣1   C、x1=1，x2=0 D、x1=1，x2=﹣1

    查看试题解析

  • 3. 抛物线y=(x−1)2+2的顶点坐标是（    ）
    A、(1 ， 2) B、(1 ， −2) C、(−1 ， 2) D、(−1 ， −2)

    查看试题解析

  • 4. 一组数据1，x，5，7的中位数与众数相等，则该组的平均数是（   ）
    A、3.5 B、4.5 C、5.5 D、6

    查看试题解析

  • 5. 若 ab=32 ，则 a−ba 中的值为（   ）
    A、13 B、12 C、23 D、34

    查看试题解析

  • 6. 如图，在△ABC中，点D、E分别是AB、AC的中点，若△ADE的面积为4，则△ABC的面积为（   ）

    A、16 B、12 C、10 D、8

    查看试题解析

  • 7. 如图，PA，PB切⊙O于点A，B，点C是⊙O上一点，且∠P＝36°，则∠ACB＝（   ）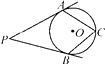


    A、54° B、72° C、108° D、144°

    查看试题解析

  • 8. 二次函数y＝ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①a＜0，②b＞0，③b2﹣4ac＞0，④a+b+c＜0，其中结论正确的个数有（ ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

  • 9. 投掷一枚质地均匀的正方体骰子，向上一面的点数是1的概率是 ．

    查看试题解析

  • 10. 二次函数y=−(x−2)2+3 ， 当1≤x≤5时，y的最小值为.

    查看试题解析

  • 11. 已知三条线段a、b、c ， 其中a=1cm ， b=4cm ， c是a、b的比例中项，则c=cm.

    查看试题解析

  • 12. 甲，乙两人进行飞镖比赛，每人各投6次.甲的成绩(单位:环)为:9，8，9.6，10，6.甲、乙两人平均成绩相等，乙成绩的方差为4.那么成绩较为稳定的是.(填“甲”或“乙“).

    查看试题解析

  • 13. 已知x=−1是关于x的方程ax2+bx−2=0的一个根，则2020+2a−2b=.

    查看试题解析

  • 14. 已知圆锥的底面圆半径为4，侧面展开图扇形的圆心角为120°，则它的侧面展开图面积为.

    查看试题解析

  • 15. 如图，△ABC内接于⊙O，OD⊥BC于D，∠A＝40°，则∠COD＝.

    查看试题解析

  • 16. 如图Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，点P为BC上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ的最小值为.

    查看试题解析

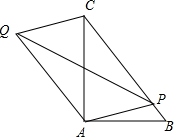
三、解答题

  • 17. 解一元二次方程：
    (1)、x2-2x-4＝0；
    (2)、（x-5）（x+2）＝8.

    查看试题解析

  • 18. 在平面直角坐标系中，△ABC的顶点坐标分别是A（-2，3），B（-3，2），C（-1，1）.

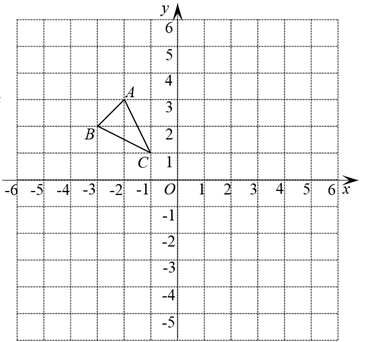
    ⑴作出△ABC关于原点O成中心对称的△A1B1C1；

    ⑵以点O为位似中心，在△ABC的同侧作出相似比为2：1，放大后的△A2B2C2.

    查看试题解析

  • 19. 教育行政部门规定初中生每天户外活动的平均时间不少于1小时，为了解学生户外活动的情况，随机地对部分学生进行了抽样调查，并将调查结果绘制成如下两幅不完整的统计图.请根据图中提供的信息解答下列问题：

    (1)、在这次调查中共调查的学生人数为；活动时间为1小时所占的比例是%.
    (2)、补全条形统计图；
    (3)、若该市共有初中生约14000名，试估计该市符合教育行政部门规定的活动时间的学生数.

    查看试题解析

  • 20. 现如今，“垃圾分类”意识已深入人心，垃圾一般可分为：可回收物、厨余垃圾、有害垃圾、其他垃圾. 现有甲、乙二人，其中甲拿了一袋垃圾，乙拿了两袋垃圾.
    (1)、直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率.
    (2)、用画树状图或列表的方法求乙所拿的垃圾不同类的概率.

    查看试题解析

  • 21. 如图，在△ABC中，点D在AB边上，∠ABC=∠ACD，

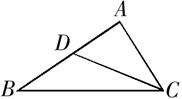    (1)、求证：△ABC∽△ACD
    (2)、若AD=2，AB=5.求AC的长．

    查看试题解析

  • 22. 如图，已知抛物线y＝x2+bx+c经过A（-1，0）、B（3，0）两点.

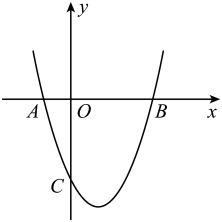    (1)、求抛物线的解析式和顶点坐标；
    (2)、当0＜x＜3时，则y的取值范围.

    查看试题解析

  • 23. 如图，△ABC是一块锐角三角形的材料，边BC＝120mm ， 高AD＝80mm ， 要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少mm ．

    查看试题解析

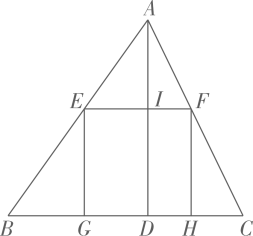  • 24. 如图，在Rt△ABC中，∠ACB＝90°，点D在AC边上，以AD为直径作⊙O交AB于点E，连接CE，且CB＝CE.

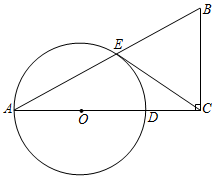    (1)、求证：CE是⊙O的切线；
    (2)、若CD＝2，AB＝45 ， 求⊙O的半径.

    查看试题解析

  • 25. 某超市销售一批成本为20元/千克的绿色健康食品，深受游客青睐．经市场调查发现，该食品每天的销售量y（千克）与销售单价x（元/千克）之间满足一次函数关系，其图像如图所示．

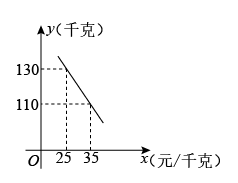    (1)、求该食品每天的销售量y（千克）与销售单价x（元/千克）之间的函数关系式；
    (2)、若超市按售价不低于成本价，且不高于40元销售，则销售单价定为多少，才能使销售该食品每天获得的利润W（元）最大？最大利润是多少？
    (3)、若超市要使每天销售该食品获得的利润不低于2400元，则每天的销售量最少应为千克．

    查看试题解析

  • 26. 问题背景：已知∠EDF的顶点D在△ABC的边AB所在直线上（不与A，B重合），DE交AC所在直线于点M，DF交BC所在直线于点N，∠B＝∠A＝∠EDF.

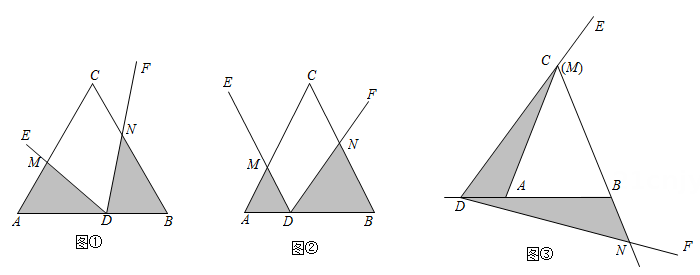    (1)、初步尝试：如图①，当△ABC是等边三角形，判断：△ADM△BND（填相似或全等）；
    (2)、类比探究：如图②，当AC＝BC时，上述结论是否还成立？请说明理由.
    (3)、延伸拓展：如图③，在（2）的条件下，当点D在BA的延长线上运动到点M与点C重合时，若S△ADM：S△BND＝1：2，BN：BM＝1：3，AD＝1，则DN＝.

    查看试题解析

  • 27. 如图，抛物线y＝ax2+2x+c与x轴交于A、B两点，且与y轴交于点C（0，3），直线y＝﹣x﹣1经过点A且与抛物线交于另一点D.

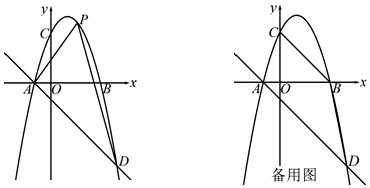    (1)、求抛物线的解析式；
    (2)、设点P是位于直线AD上方的抛物线上的一个动点，连接PA、PD，求△PAD的面积的最大值；
    (3)、Q点在x轴上且位于点B的左侧，若以Q，B，C为顶点的三角形与△ABD相似，求点Q的坐标.

    查看试题解析