广西壮族自治区南宁市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-12-14 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为（）

A、 $46 \times 10^{- 7}$ B、 $4.6 \times 10^{- 7}$ C、 $4.6 \times 10^{- 6}$ D、 $0.46 \times 10^{- 5}$

查看试题解析
3. 在平面直角坐标系中，点 $P (1 ， 2)$ 关于 $x$ 轴对称的点为 $P'$ ，则点 $P'$ 的坐标为（）

A、 $(2 ， 1)$ B、 $(- 1 ， 2)$ C、 $(1 ， - 2)$ D、 $(- 1 ， - 2)$

查看试题解析
4. 下列长度的线段中，能组成三角形的是（）

A、4，6，8 B、1，2，4 C、5，6，12 D、2，3，5

查看试题解析
5. 一个n边形的各内角都等于 $120 °$ ，则n等于（）

A、5 B、6 C、7 D、8

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 是高，能直接判断 $△ A B D ≅ △ A C D$ 的依据是（）

A、 $S S S$ B、 $S A S$ C、 $H L$ D、 $A S A$

查看试题解析
7. 把分式 $\frac{x}{x + y}$ 中的 $x$ ， $y$ 都扩大5倍，则分式的值（）

A、扩大5倍 B、扩大10倍 C、缩小一半 D、不变

查看试题解析
8. 下列计算正确的是（）

A、 $x^{3} \cdot x^{3} = 2 x^{3}$ B、 ${(x^{3})}^{2} = x^{5}$ C、 $2^{- 2} = - 4$ D、 $x y^{2} \div y = x y$

查看试题解析
9. 现有甲、乙、丙三种不同的长方形纸片若干张（边长如图）.小明要用这三种纸片紧密拼接成一个没有缝隙的大正方形，他选取甲纸片1张，再取乙纸片4张，还需要取丙纸片的张数为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 一项工程，甲单独做要x天完成，乙单独做要y天完成，则甲、乙合做完成工程需要的天数为（）

A、 $\frac{x y}{x + y}$ B、 $\frac{x + y}{2}$ C、 $\frac{x + y}{x y}$ D、 $x + y$

查看试题解析
11. 如图在长方形台球桌上打台球时，球的入射角 $∠ 1$ 等于反射角 $∠ 2$ .如果击打白球时入射角 $∠ 1 = 30 °$ ，恰好使白球在上边框的点 $A$ 处反弹后进入袋中，点 $A$ 到右边框 $B C$ 的距离为3，则白球从点 $A$ 到进袋所走过的路径 $A C$ 约为（）

A、3 B、4 C、5 D、6

查看试题解析
12. 已知 $△ A B C$ 是边长为10的等边三角形， $D$ 为 $A C$ 的中点， $∠ E D F = 120 °$ ， $D E$ 交线段 $A B$ 于 $E$ ， $D F$ 交 $B C$ 的延长线于 $F$ .若 $A E = 4 B E$ ，则 $C F$ 的长为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 要使分式 $\frac{1}{x + 3}$ 有意义，则x的取值范围为．

查看试题解析
14. 如图，为了防止门板变形，小明在门板上钉了一根加固木条，请用数学知识说明这样做的依据.

查看试题解析
15. 因式分解： $x^{2} y - 9 y =$ .

查看试题解析
16. 若 ${(x - \frac{1}{3})}^{2}$ 展开后等于 $x^{2} - a x + \frac{1}{9}$ ，则 $a$ 的值为.

查看试题解析
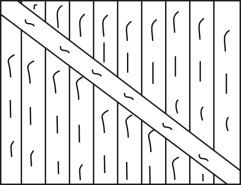17. “共和国勋章”获得者、“杂交水稻之父”袁隆平培育的杂交水稻解决了全球多个国家的温饱问题.某试验基地现有 $A$ 、 $B$ 两块试验田，分别种植甲、乙两种杂交水稻，今年两块实验田分别收获了24吨和30吨水稻.已知甲种杂交水稻的亩产量是乙种杂交水稻的亩产量的1.2倍， $A$ 块试验田比 $B$ 块试验田少10亩，设乙种杂交水稻的亩产量是 $x$ 吨，则可列得的方程为.

查看试题解析
18. 已知一张三角形纸片 $A B C$ （如图甲），其中 $A B = A C = 10$ ， $B C = 6$ .将纸片沿 $D E$ 折叠，使点 $A$ 与点 $B$ 重合（如图乙）时， $C E = a$ ；再将纸片沿 $E F$ 折叠，使得点 $C$ 恰好与 $B E$ 边上的 $G$ 点重合，折痕为 $E F$ （如图丙），则 $△ B F G$ 的周长为（用含 $a$ 的式子表示）.

查看试题解析

三、解答题

19. 化简： ${(- x y)}^{2} \cdot y - 3 x y \cdot x y^{2}$ .

查看试题解析
20. 先化简，再求值 $(a - \frac{2 a - 1}{a}) \div \frac{a - 1}{a}$ ，其中 $a = 2023$ .

查看试题解析
21. 在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 36 °$ .

(1)、尺规作图：求作 $A B$ 边的垂直平分线分别交 $A B$ ， $A C$ 于点 $D$ 和点 $E$ ﹔（保留作图痕迹，不要求写出作图过程）

(2)、直接写出 $△ B C E$ 的形状.

查看试题解析
22. 如图，点B，E，C，F在一条直线上，AC与DE相交于点O，AB=DE，AB∥DE，BE=CF.

(1)、求证： $A C ∥ D F$ ；

(2)、若 $∠ B = 65 °$ ， $∠ F = 35 °$ ，求 $∠ E O C$ 的度数.

查看试题解析
23. 2021年12月，我市某区千亩“三月红”柑橘挂满枝头，采摘人员的需求也随之增多，为了尽快抢收成熟柑橘，某脱贫攻坚办公室紧急组织了一支志愿者服务队.某村种植合作社共需要采摘柑橘240吨，村民采摘40吨后，志愿者服务队加入一起采摘.已知志愿者服务队采摘的速度是村民采摘速度的1.5倍，从村民开始采摘到全部采摘完毕，一共用了15天.

(1)、求村民每天采摘柑橘多少吨？

(2)、已知合作社每天需要支出给村民劳务费2000元，志愿者服务队是义务劳动，不需支出劳务费，只需每天支出饮食费500元，问志愿者服务队加入后可帮助合作社节省多少元？

查看试题解析
24. 等面积法是一种常用的、重要的数学解题方法.

(1)、如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 3$ ， $A C = 4$ ， $A B = 5$ ， $C D ⊥ A B$ ，则 $C D$ 长为；

(2)、如图2，在 $△ A B C$ 中， $A B = 4$ ， $B C = 2$ ，则 $△ A B C$ 的高 $C D$ 与 $A E$ 的比是；

(3)、如图3，在 $△ A B C$ 中， $∠ C = 90 °$ （ $∠ A < ∠ A B C$ ），点 $D$ ， $P$ 分别在边 $A B$ ， $A C$ 上，且 $B P = A P$ ， $D E ⊥ B P$ ， $D F ⊥ A P$ ，垂足分别为点 $E$ ， $F$ .若 $B C = 5$ ，求 $D E + D F$ 的值.

查看试题解析
25. 【阅读理解】
若 $x$ 满足 $(45 - x) (x - 15) = 200$ ，求 ${(45 - x)}^{2} + {(x - 15)}^{2}$ 的值.
解：设 $45 - x = a$ ， $x - 15 = b$ ，则 $(45 - x) (x - 15) = a b = 200$ ，
$a + b = (45 - x) + (x - 15) = 30$ ，
$(45 - x)^{2} + (x - 15)^{2} = a^{2} + b^{2} = (a + b)^{2} - 2 a b = 3 0^{2} - 2 \times 200 = 500$ ，
我们把这种方法叫做换元法.利用换元法达到简化方程的目的，体现了转化的数学思想.
【解决问题】

(1)、若 $x$ 满足 $(20 - x) (x - 5) = 50$ ，则 ${(20 - x)}^{2} + {(x - 5)}^{2} =$ ；

(2)、若 $x$ 满足 ${(2022 - x)}^{2} + {(x - 2000)}^{2} = 244$ ，求 $(2022 - x) (x - 2000)$ 的值；

(3)、如图，在长方形 $A B C D$ 中， $A B = 12 c m$ ，点 $E$ ， $F$ 是 $B C$ ， $C D$ 上的点， $E C = 8 c m$ ，且 $B E = D F = x$ ，分别以 $F C$ ， $C B$ 为边在长方形 $A B C D$ 外侧作正方形 $C F G H$ 和 $C B M N$ ，若长方形 $C B Q F$ 的面积为 $60 c m^{2}$ ，求图中阴影部分的面积和.

查看试题解析
26. 如图1，分别以 $△ A B C$ 的两边 $A B$ ， $A C$ 为边作 $△ A B D$ 和 $△ A C E$ ，使得 $A B = A D$ ， $A E = A C$ ， $∠ D A B = ∠ E A C$ .

(1)、求证： $B E = C D$ ；

(2)、过点 $A$ 分别作 $A F ⊥ C D$ 于点 $F$ ，作 $A G ⊥ B E$ ，
①如图2，连接 $F G$ ，请判断 $△ A F G$ 的形状，并说明理由；

②如图3，若 $C D$ 与 $B E$ 相交于点 $H$ ，且 $∠ D A B = ∠ E A C = 60 °$ ，试猜想 $A H$ ， $C H$ ， $H E$ 之间的数量关系，并证明.

查看试题解析