2022~2023学年中考数学一轮复习专题16最值问题
试卷更新日期:2022-12-14 类型:一轮复习
一、轴对称最值问题
-
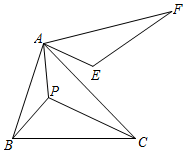
1. 如图,在中, , 、是的两条中线, , P是上一个动点,则的最小值是( )
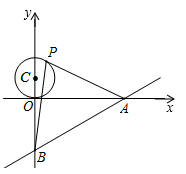
 A、7 B、3.5 C、5 D、2.52. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
A、7 B、3.5 C、5 D、2.52. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、3. 如图,在矩形ABCD中, ,E,F分别是AD,AB的中点, 的平分线交AB于点G,点P是线段DG上的一个动点,则 的周长最小值为.
A、 B、 C、 D、3. 如图,在矩形ABCD中, ,E,F分别是AD,AB的中点, 的平分线交AB于点G,点P是线段DG上的一个动点,则 的周长最小值为.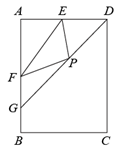 4. 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE最小值是( )
4. 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE最小值是( )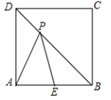 A、 B、 C、 D、5. 如图,正方形ABCD的边长是4,点E是DC上一个点,且DE=1,P点在AC上移动,则PE+PD的最小值是( )
A、 B、 C、 D、5. 如图,正方形ABCD的边长是4,点E是DC上一个点,且DE=1,P点在AC上移动,则PE+PD的最小值是( )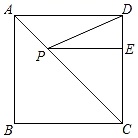 A、4 B、4.5 C、5.5 D、56. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .
A、4 B、4.5 C、5.5 D、56. 如图,有一张平行四边形纸片 , , , 将这张纸片折叠,使得点落在边上,点的对应点为点 , 折痕为 , 若点在边上,则长的最小值等于 .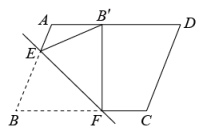 7. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 .
7. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 .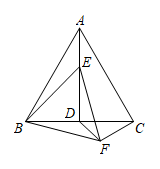 8. 如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE + PF的最小值是( )
8. 如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE + PF的最小值是( ) A、2 B、 C、1.5 D、9. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )
A、2 B、 C、1.5 D、9. 如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,点E,F的坐标分别为( )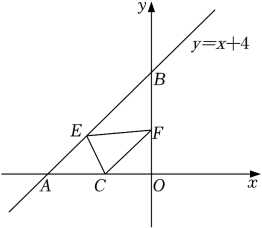 A、 , B、 , C、 , D、 ,10. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.
A、 , B、 , C、 , D、 ,10. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.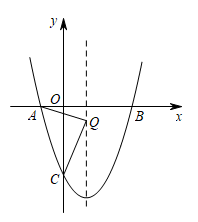 (1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.
(1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.二、隐含圆问题
-
11. 如图, 中, , , .点 为 内一点,且满足 .当 的长度最小时, 的面积是( )
 A、3 B、 C、 D、12. 如图,在△ABC中, , BC=3,AC=4,点D是AC边上一动点,过点A作交BD的延长线于点E,则的最小值为.
A、3 B、 C、 D、12. 如图,在△ABC中, , BC=3,AC=4,点D是AC边上一动点,过点A作交BD的延长线于点E,则的最小值为.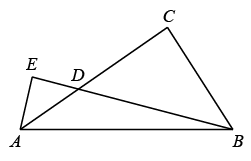 13. 如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值( )
13. 如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值( ) A、4 B、8 C、10 D、614. 如图,是的外接圆,为直径,若 , , 点从点出发,在内运动且始终保持 , 当 , 两点距离最小时,动点的运动路径长为 .
A、4 B、8 C、10 D、614. 如图,是的外接圆,为直径,若 , , 点从点出发,在内运动且始终保持 , 当 , 两点距离最小时,动点的运动路径长为 . 15. △ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.
15. △ABC是边长为5的等边三角形,△DCE是边长为3的等边三角形,直线BD与直线AE交于点F.如图,若点D在△ABC内,∠DBC=20°,则∠BAF=°;现将△DCE绕点C旋转1周,在这个旋转过程中,线段AF长度的最小值是.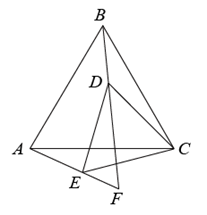 16. 如图,正方形ABCD的边长为16,点E,F分别在线段AB,AD上,且AF=8,AE=6,若点P,Q分别在线段BC,CD上运动,G为线段PF上的点,在运动过程中,始终保持∠GEB=∠GFA,则线段GQ的最小值为.
16. 如图,正方形ABCD的边长为16,点E,F分别在线段AB,AD上,且AF=8,AE=6,若点P,Q分别在线段BC,CD上运动,G为线段PF上的点,在运动过程中,始终保持∠GEB=∠GFA,则线段GQ的最小值为. 17. 如图,在 中, , , , 是 上方一动点,且 , 交 于点E.当点P运动到 时, 的值为;随着点P的运动, 的最大值为.
17. 如图,在 中, , , , 是 上方一动点,且 , 交 于点E.当点P运动到 时, 的值为;随着点P的运动, 的最大值为. 18. 如图,△ABC中,AB=AC= ,∠BAC=α°, ,G为BC中点,D为平面内一个动点,且 .将线段BD绕点D逆时针旋转α°,得到DB′,则四边形BACB′面积的最大值为( )
18. 如图,△ABC中,AB=AC= ,∠BAC=α°, ,G为BC中点,D为平面内一个动点,且 .将线段BD绕点D逆时针旋转α°,得到DB′,则四边形BACB′面积的最大值为( )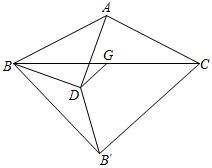 A、24 B、25 C、12 D、1319. 如图,在 中, ∠ACB=90°, cm, cm. 是 边上的一个动点,连接 ,过点 作 于 ,连接 ,在点 变化的过程中,线段 的最小值是( )
A、24 B、25 C、12 D、1319. 如图,在 中, ∠ACB=90°, cm, cm. 是 边上的一个动点,连接 ,过点 作 于 ,连接 ,在点 变化的过程中,线段 的最小值是( )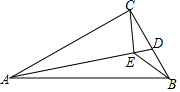 A、1 B、 C、2 D、
A、1 B、 C、2 D、三、造桥选址问题
-
20. 如图,正方形ABCD的对角线上的两个动点M、N,满足 , 点P是BC的中点,连接AN、PM,若 , 则当的值最小时,线段AN的长度为 .
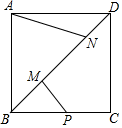 21. 如图,矩形ABCD中,AD=2,AB=4,AC为对角线,E、F分别为边AB、CD上的动点,且EF⊥AC于点M,连接AF、CE,求AF+CE的最小值是 .
21. 如图,矩形ABCD中,AD=2,AB=4,AC为对角线,E、F分别为边AB、CD上的动点,且EF⊥AC于点M,连接AF、CE,求AF+CE的最小值是 . 22. 如图,矩形 中, , , 在边 上运动, 、 在对角线 上运动,且 ,连接 、 ,则 的最小值为.
22. 如图,矩形 中, , , 在边 上运动, 、 在对角线 上运动,且 ,连接 、 ,则 的最小值为.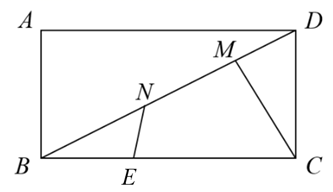 23. 在矩形ABCD中,AB=4,BC=2,E为BC中点,H,G分别是边AB,CD上的动点,且始终保持GH⊥AE,则EH+AG最小值为.
23. 在矩形ABCD中,AB=4,BC=2,E为BC中点,H,G分别是边AB,CD上的动点,且始终保持GH⊥AE,则EH+AG最小值为.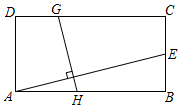 24. 如图,定直线MNPQ,点B、C分别为MN、PQ上的动点,且BC=12,BC在两直线间运动过程中始终有∠BCQ=60°.点A是MN上方一定点,点D是PQ下方一定点,且AEBCDF,AE=4,DF=8,AD=24 , 当线段BC在平移过程中,AB+CD的最小值为( )
24. 如图,定直线MNPQ,点B、C分别为MN、PQ上的动点,且BC=12,BC在两直线间运动过程中始终有∠BCQ=60°.点A是MN上方一定点,点D是PQ下方一定点,且AEBCDF,AE=4,DF=8,AD=24 , 当线段BC在平移过程中,AB+CD的最小值为( )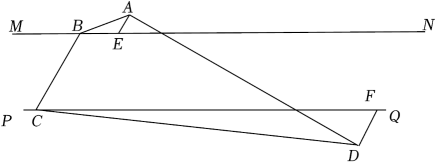 A、24 B、24 C、12 D、12
A、24 B、24 C、12 D、12四、胡不归最值问题
-
25. 如图,在平面直角坐标系中,抛物线的顶点为A点,且与x轴的正半轴交于点B,P点是该抛物线对称轴上的一点,则的最小值为( )
 A、 B、 C、 D、26. 图所示,在半径为 6 的扇形 ABC 中, ∠BAC=60° ,点 D ,E 分别在半径 AB,AC 上,且BD=CE=2,点F 是弧BC 上的动点,连接DF,EF,则DF+ EF 的最小值为.
A、 B、 C、 D、26. 图所示,在半径为 6 的扇形 ABC 中, ∠BAC=60° ,点 D ,E 分别在半径 AB,AC 上,且BD=CE=2,点F 是弧BC 上的动点,连接DF,EF,则DF+ EF 的最小值为.
五、瓜豆原理最值问题
-
27. 如图,在矩形中, , , 点P在线段上运动(含B、C两点),连接 , 以点A为中心,将线段逆时针旋转60°到 , 连接 , 则线段的最小值为( )
 A、 B、 C、 D、328. 如图,正方形ABCD的边长为4, , 点E是直线CM上一个动点,连接BE,线段BE绕点B顺时针旋转45°得到BF,连接DF,则线段DF长度的最小值等于( )
A、 B、 C、 D、328. 如图,正方形ABCD的边长为4, , 点E是直线CM上一个动点,连接BE,线段BE绕点B顺时针旋转45°得到BF,连接DF,则线段DF长度的最小值等于( ) A、 B、 C、 D、29. 如图,、 , 以为直径作 , 射线交于、两点,为弧的中点,为的中点.当射线绕点旋转时,的最小值为 .
A、 B、 C、 D、29. 如图,、 , 以为直径作 , 射线交于、两点,为弧的中点,为的中点.当射线绕点旋转时,的最小值为 .
六、阿氏圆最值问题
-
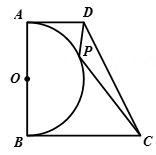
30. 如图,在直角梯形ABCD中,∠ABC=∠DAB=90°,AB=BC=4,AD=2,点P是以AB为直径的半圆O上一点,连接PC、PD,则PC+ PD的最小值为.
 31. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则PA+PB的最小值为 .
31. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=4,以点C为圆心,3为半径做⊙C,分别交AC,BC于D,E两点,点P是⊙C上一个动点,则PA+PB的最小值为 .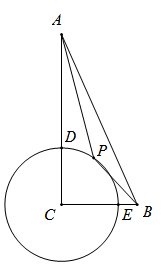 32. 如图,在Rt△ABC中,∠ACB=90°,CB=7,AC=9,以C为圆心、3为半径作⊙C,P为⊙C上一动点,连接AP、BP,则AP+BP的最小值为( )
32. 如图,在Rt△ABC中,∠ACB=90°,CB=7,AC=9,以C为圆心、3为半径作⊙C,P为⊙C上一动点,连接AP、BP,则AP+BP的最小值为( ) A、3. B、4 C、3 D、533. 如图,中, , , , , 为 , 边上的两个动点,且 , 为中点,则的最小值为( )
A、3. B、4 C、3 D、533. 如图,中, , , , , 为 , 边上的两个动点,且 , 为中点,则的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、七、二次函数最值问题
-
34. 如图1,在菱形ABCD中,∠C=120°,M是AB的中点,N是对角线BD上一动点,设DN长为x,线段MN与AN长度的和为y,图2是y关于x的函数图象,图象右端点F的坐标为 , 则图象最低点E的坐标为( )
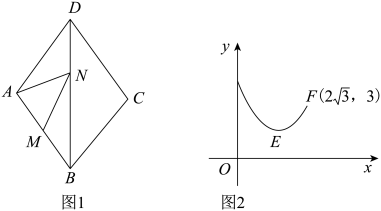 A、 B、 C、 D、35. 如图,点E是矩形边上一点,沿折叠,点恰好落在边上的点处,设 ,
A、 B、 C、 D、35. 如图,点E是矩形边上一点,沿折叠,点恰好落在边上的点处,设 , (1)、若点恰为边的中点,则.(2)、设 , 则y关于的函数表达式是.36. 已知实数m,n满足 , 则的最大值为( )A、24 B、 C、 D、-437. 如图所示,在菱形ABCD中,AB=6,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( )
(1)、若点恰为边的中点,则.(2)、设 , 则y关于的函数表达式是.36. 已知实数m,n满足 , 则的最大值为( )A、24 B、 C、 D、-437. 如图所示,在菱形ABCD中,AB=6,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,△CEF的面积最大值是( ) A、4 B、 C、3 D、38. 如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A、4 B、 C、3 D、38. 如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )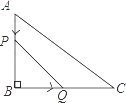 A、18cm2 B、12cm2 C、9cm2 D、3cm2
A、18cm2 B、12cm2 C、9cm2 D、3cm2八、其它问题(费马定理,线圆最值)