浙江省宁波市北仑区联考2022-2023学年八年级上学期期中数学试卷
试卷更新日期:2022-12-14 类型:期中考试
一、选择题(本大题共10小题,共30分)
-
1. 下列四个手机图标中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,四个图形中,线段BE是△ABC的高的图是( )A、
2. 如图,四个图形中,线段BE是△ABC的高的图是( )A、 B、
B、 C、
C、 D、
D、 3. 若 ,则下列式子中,错误的是( )A、 B、 C、 D、4. 已知等腰三角形中, , , 则这个三角形的周长为( )A、16 B、18 C、20 D、16或205. △ABC的三个内角∠A,∠B,∠C满足∠A:∠B:∠C=3:4:5,则这个三角形是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形6. 下列命题是真命题的是A、相等的角是对顶角 B、若实数 , 满足 ,则 C、若实数 , 满足 , ,则 D、两直线平行,内错角相等7. 一副三角板如图所示摆放,则 与 的数量关系为( )
3. 若 ,则下列式子中,错误的是( )A、 B、 C、 D、4. 已知等腰三角形中, , , 则这个三角形的周长为( )A、16 B、18 C、20 D、16或205. △ABC的三个内角∠A,∠B,∠C满足∠A:∠B:∠C=3:4:5,则这个三角形是( )A、锐角三角形 B、钝角三角形 C、直角三角形 D、等腰三角形6. 下列命题是真命题的是A、相等的角是对顶角 B、若实数 , 满足 ,则 C、若实数 , 满足 , ,则 D、两直线平行,内错角相等7. 一副三角板如图所示摆放,则 与 的数量关系为( )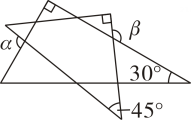 A、 B、 C、 D、8. 如图,和的平分线交于点 , 过点作分别交 , 于点 , , 若 , , 则线段的长为( )
A、 B、 C、 D、8. 如图,和的平分线交于点 , 过点作分别交 , 于点 , , 若 , , 则线段的长为( ) A、16 B、17 C、18 D、199. 如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AC=3cm,则BE等于( ).
A、16 B、17 C、18 D、199. 如图所示,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AC=3cm,则BE等于( ). A、 B、 C、 D、10. 如图的中, , 且为上一点.今打算在上找一点 , 在上找一点 , 使得与全等,以下是甲、乙两人的作法:
A、 B、 C、 D、10. 如图的中, , 且为上一点.今打算在上找一点 , 在上找一点 , 使得与全等,以下是甲、乙两人的作法:甲连接 , 作的中垂线分别交、于点、点,则、两点即为所求
乙过作与平行的直线交于点,过作与平行的直线交于点,则、两点即为所求
对于甲、乙两人的作法,下列判断何者正确?( )
 A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确
A、两人皆正确 B、两人皆错误 C、甲正确,乙错误 D、甲错误,乙正确二、填空题(本大题共6小题,共24分)
-
11. 根据数量关系“a是正数”,可列出不等式: .12. 命题“等腰三角形的两个底角相等.”的逆命题是 .13. 在中, , , 则为 度14. 如图,已知中, , 平分 , 点是的中点,若 , 则的长为.
 15. 如图,中, , , , 点为边上的动点,过点作于点 , 则的最小值为.
15. 如图,中, , , , 点为边上的动点,过点作于点 , 则的最小值为. 16. 如图,在矩形中, , , 、分别是边、上一点, , 将沿翻折得 , 连接 , 当 时,是以为腰的等腰三角形.
16. 如图,在矩形中, , , 、分别是边、上一点, , 将沿翻折得 , 连接 , 当 时,是以为腰的等腰三角形.
三、解答题(本大题共8小题,共66分)
-
17. 解不等式,并将解集在数轴上表示出来.(1)、;(2)、.18. 如图,已知在中, , , , 请在三角形的边上找一点 , 并过点和三角形的一个顶点画一条线段,将这个三角形分成两个等腰三角形.要求两种不同的分法并写出每个等腰三角形的内角度数
 19. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
19. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求: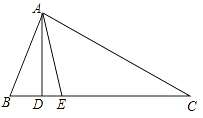 (1)、∠BAE的度数;(2)、∠DAE的度数;20. 已知,如图,点、、、在同一直线上, , ,
(1)、∠BAE的度数;(2)、∠DAE的度数;20. 已知,如图,点、、、在同一直线上, , , (1)、求证:≌;(2)、当 , 求的度数.21. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米,小区为美化环境,欲在空地上铺草坪.
(1)、求证:≌;(2)、当 , 求的度数.21. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米,小区为美化环境,欲在空地上铺草坪. (1)、是直角三角形吗?为什么?(2)、小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?22. 两种不同的方法证明已知,如图 , 在的边上, , ,
(1)、是直角三角形吗?为什么?(2)、小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?22. 两种不同的方法证明已知,如图 , 在的边上, , ,
求证:.
方法一: ;
方法二: .

