浙江省丽水市青田县八校联考2022-2023学年九年级上学期期中数学试卷
试卷更新日期:2022-12-14 类型:期中考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 下列事件,是随机事件的是( )A、太阳从东方升起 B、买一张体育彩票中奖 C、两个负数相加,和是负数 D、口袋中装有10个红球,从中摸出一个白球2. 抛物线的顶点坐标是( )A、 B、 C、 D、3. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、154. 若二次函数配方后为 , 则的值分别为( )A、0 B、5 C、6 D、-65. 已知 , 是抛物线图象上两点,则 , 的大小关系( )A、 B、 C、 D、无法确定6. 把抛物线向右平移1个单位,再向下平移2个单位,所得抛物线是( )A、 B、 C、 D、7. 如图,在中, , 将绕点按逆时针方向旋转得 , 且点在上,交于点 , 则的度数为
 ( )
( )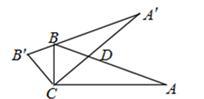 A、 B、 C、 D、8. 如图,二次函数与一次函数的图象交于点和点 , 要使 , 则的取值范围是( )
A、 B、 C、 D、8. 如图,二次函数与一次函数的图象交于点和点 , 要使 , 则的取值范围是( )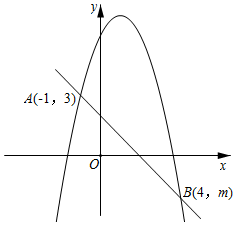 A、 B、 C、 D、或9. 如图,在圆中,弦 , 点在上移动,连接 , 过点做交圆于点 , 则的最大值为( )
A、 B、 C、 D、或9. 如图,在圆中,弦 , 点在上移动,连接 , 过点做交圆于点 , 则的最大值为( )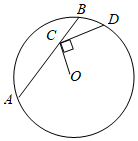 A、 B、2 C、 D、10. 二次函数的最大值是零,那么代数式的化简结果是( )A、 B、 C、1 D、0
A、 B、2 C、 D、10. 二次函数的最大值是零,那么代数式的化简结果是( )A、 B、 C、1 D、0二、填空题(本大题共6小题,共18.0分)
-
11. 已知的半径为5,点到圆心的距离是4,则点与的位置关系是.12. 在-3,-2,1,2,3五个数中随机选取一个数作为二次函数中的值,则该二次函数图象开口向上的概率是.13. 二次函数 的图象经过点 ,则c的值为.14. 如图,AB是⊙O的弦,AB长为4,P是⊙O上一个动点(不与A、B重合).过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长为.
 15. 如图,在平面直角坐标系中,菱形的顶点在轴负半轴上,顶点在轴正半轴上.若抛物线经过点、 , 则点的坐标为.
15. 如图,在平面直角坐标系中,菱形的顶点在轴负半轴上,顶点在轴正半轴上.若抛物线经过点、 , 则点的坐标为.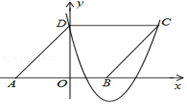 16. 已知点 、 是半径为 的 上两点,且 ,点 是 上一个动点,点 是 的中点,连接 ,则 的最小值是.
16. 已知点 、 是半径为 的 上两点,且 ,点 是 上一个动点,点 是 的中点,连接 ,则 的最小值是.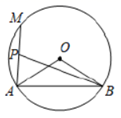
三、解答题(本大题共8小题,共52.0分。骤)
-
17. 甲、乙、丙、丁4人聚会,吗,每人带了一件礼物,4件礼物从外盒包装看完全相同,将4件礼物放在一起.(1)、甲从中随机抽取一件,则甲抽到不是自己带来的礼物的概率是;(2)、甲先从中随机抽取一件,不放回,乙再从中随机抽取一件,求甲、乙2人抽到的都不是自己带来的礼物的概率.18. 已知抛物线 经过点 .(1)、求 的值及抛物线的顶点坐标;(2)、当 取什么值时, 随着 的增大而减小?19. 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.由于该十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为 ,向左转和直行的频率均为 .(1)、假设平均每天通过该路口的汽车为5000辆,求汽车在此左转、右转、直行的车辆各是多少辆;(2)、目前在此路口,汽车左转、右转、直行的绿灯亮的时间均为30秒,在绿灯总时间不变的条件下,为了缓解交通拥挤,请你利用概率的知识对此路口三个方向的绿灯亮的时间做出合理的调整.20. 如图,已知抛物线与坐标轴交于 , , 三点,其中 , .
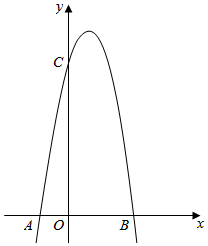 (1)、求该抛物线的表达式;(2)、根据图象,直接写出时,的取值范围;(3)、若要使抛物线与轴只有一个交点,则需将抛物线向下平移几个单位?21. “筒车”是一种以水流作动力,取水灌田的工具.明朝科学家徐光启在农政全书中用图画描绘了“筒车”的工作原理.如图,“筒车”盛水筒的运行轨迹是以轴心为圆心的圆,已知圆心始终在水面上方,且当圆被水面截得的弦为6米时,水面下盛水筒的最大深度为1米即水面下方部分圆上一点距离水面的最大距离.
(1)、求该抛物线的表达式;(2)、根据图象,直接写出时,的取值范围;(3)、若要使抛物线与轴只有一个交点,则需将抛物线向下平移几个单位?21. “筒车”是一种以水流作动力,取水灌田的工具.明朝科学家徐光启在农政全书中用图画描绘了“筒车”的工作原理.如图,“筒车”盛水筒的运行轨迹是以轴心为圆心的圆,已知圆心始终在水面上方,且当圆被水面截得的弦为6米时,水面下盛水筒的最大深度为1米即水面下方部分圆上一点距离水面的最大距离.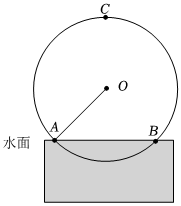 (1)、求该圆的半径;(2)、若水面上涨导致圆被水面截得的弦从原来的6米变为8米时,则水面下盛水筒的最大深度为多少米?22. 某市人民广场上要建造一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.
(1)、求该圆的半径;(2)、若水面上涨导致圆被水面截得的弦从原来的6米变为8米时,则水面下盛水筒的最大深度为多少米?22. 某市人民广场上要建造一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.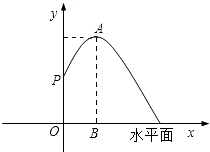 (1)、求这条抛物线的解析式;
(1)、求这条抛物线的解析式;
(2)、若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?23. “新冠肺炎”疫情期间某工厂为支持国家抗击疫情每天连夜生产急缺的消毒液,已知每瓶消毒液的生产成本为20元,为了合理定价,根据市场调查发现,当销售单价为30元时,每天的销售量为6000瓶,若销售单价每降低1元,则每天能多销售1000瓶,但要求销售单价不能低于成本且不高于30元.(1)、求每天的销售量 (瓶)与销售单价 (元)之间的函数关系式;(2)、求每天的利润 (元)与销售单价 (元)之间的函数关系式;(3)、该工厂负责人决定将每天的利润全部捐献出来进一步支持国家抗击“新冠肺炎”疫情,则当销售单价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图,抛物线与轴交于点 , 点 , 与轴交于点 , 点与点关于轴对称,点是抛物线上的一个动点.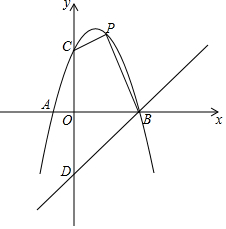 (1)、求直线的解析式;(2)、当点在第一象限时,求四边形面积的最大值,并求出此时点的坐标;(3)、在点的运动过程中,是否存在点 , 使是以为直角边的直角三角形?若存在,求出点的坐标;若不存在,请说明理由.
(1)、求直线的解析式;(2)、当点在第一象限时,求四边形面积的最大值,并求出此时点的坐标;(3)、在点的运动过程中,是否存在点 , 使是以为直角边的直角三角形?若存在,求出点的坐标;若不存在,请说明理由.