浙江省丽水市青田县八校联考2022-2023学年八年级上学期期中数学试卷
试卷更新日期：2022-12-14 类型：期中考试
一、选择题（本题有10小题，每小题3分，共30分.）
-
1. 已知三角形的两边长分别是5cm和10cm，则下列长度的线段中能作为第三边的是（ ）A、4cm B、5cm C、10cm D、15cm2. 如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（ ）A、
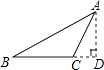B、
C、
D、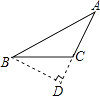
3. 下列语句是命题的是（ ）A、作直线AB的垂线 B、在线段AB上取点C C、垂线段最短吗？ D、同旁内角互补4. 如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（ ）
A、两点之间的线段最短 B、三角形具有稳定性 C、长方形是轴对称图形 D、长方形的四个角都是直角5.用直尺和圆规作一个角等于已知角的作图痕迹如图所示，则作图的依据是（）
A、SSS B、SAS C、ASA D、AAS6. 适合下列条件的△ABC中，直角三角形的个数为（ ）①∠A：∠B：∠C＝1：2：3；②∠A+∠B＝∠C；③∠A＝90°-∠B；④∠A＝∠B＝2∠C.
A、1 B、2 C、3 D、47. 如图，四个全等的直角三角形和中间的小正方形可以拼成一个大正方形，若直角三角形的较长直角边长为a，较短直角边长为b，大正方形面积为S1 ， 小正方形面积为S2 ， 则（a+b）2可表示为（ ）
A、S1-S2 B、2S1-S2 C、S1+S2 D、S1+2S28. 如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是线段AD上的动点，E是AC边上一点.若AE＝2，当EF+CF取得最小值时，∠ECF的度数为（ ）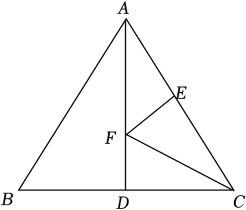
A、30° B、45° C、25° D、20°9. 如图，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且△ABC的面积是4，则△BEF的面积等于（ ）
A、0.75 B、1.25 C、2 D、110. 如图，在格点中找一点C，使得△ABC是等腰三角形，且AB为其中一条腰，这样的点C个数为（ ）
A、8 B、9 C、10 D、11二、填空题（本题有6小题，每小题3分，共18分）
-
11. 把命题“对顶角相等”改写成“如果…那么…”的形式：12. 在等腰△ABC中，∠A＝70°，则∠B的度数是 .13. 如图，在△ABC中，AB的中垂线DE交AC于点D，已知BC＝10，△BDC的周长为25，则AC＝.
14. 在△ABC中，AB＝AC＝5，BC＝6.若点P在边AC上移动，则BP的最小值是 .
15. 如图，∠ABC＝∠ACB，AD，BD，CD分别平分△ABC的外角∠EAC，内角∠ABC，外角∠ACF；则以下结论：①AD∥BC；②∠ACB＝2∠ADB；③∠ADC+∠ABD＝90°；其中正确的结论有 .
16. 如图，在△ABC中，AB＝10，AC＝6，则BC边上的中线AD的取值范围是.
三、解答题（本题有8小题，第17、18题5分，19～21题6分，22题7分，23题8分，24题9分，共52分，各小题都必须写出解答过程）
-
17. 如图，在△ABC中，∠BAC＝100°，AD⊥BC于D点，AE平分∠BAC交BC于点E.若∠C＝25°，求∠DAE的度数.
18. 如图，点B，F，C，E在同一条直线上，点A，D在直线BC的异侧，AB＝DE，AC＝DF，BF＝EC.
(1)、求证：△ABC≌△DEF；(2)、若∠BFD＝130°，求∠ACB的度数.19. 如图，在△ABC中，点E在AB边上，请用直尺和圆规求作一点F，使得FE＝FA，且F点到AB和BC的距离相等.（保留作图痕迹，不写作法）
20. 如图，已知P点是∠AOB平分线上一点，PC⊥OA，PD⊥OB，垂足为C、D.
(1)、求证：∠PCD＝∠PDC；(2)、求证：OP垂直平线段CD.21. 如图，已知在Rt△ABC中，∠ACB＝90°，AC＝9，BC＝12，AB的垂直平分线交AB于点D，交BC于点E，连结AE，求BE的长.
22. 如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，AD与BE交于点F，AD＝BD，
求证：
(1)、△ACD≌△BFD；(2)、BF＝2AE.23. 如图，已知等腰△ABC中，AB＝AC，∠A＜90°，CD是△ABC的高，BE是∠ABC的角平分线，CD与BE交于点P.
(1)、当∠A＝52°时，求∠BPC的度数；(2)、当∠A＝x°时，求∠BPC的度数（请用含x的代数式表示），并说明理由.24. 已知△ABC和△ADE是等腰直角三角形，∠ACB＝∠ADE＝90°，F为BE的中点，连结DF，CF.
(1)、如图①，当点D在AB上，点E在AC上，请写出此时线段DF，CF的数量关系和位置关系，并说明理由.(2)、如图②，在（1）的条件下将△ADE绕点A顺时针旋转45°，请你判断此时（1）中的结论是否仍然成立，并证明你的判断.