浙江省嘉兴市桐乡六中教育集团三校联考2022-2023学年八年级上学期期中数学试卷
试卷更新日期:2022-12-14 类型:期中考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 观察下列图案,其中与如图全等的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 已知三角形的两条边长分别为和 , 则第三条边长可以是( )A、 B、 C、 D、3. 已知在中, , , 则的度数是( )A、 B、 C、 D、4. 将一平板保护套展开放置在水平桌面上,其侧面示意图如图所示,若 , , 则的长为( )
2. 已知三角形的两条边长分别为和 , 则第三条边长可以是( )A、 B、 C、 D、3. 已知在中, , , 则的度数是( )A、 B、 C、 D、4. 将一平板保护套展开放置在水平桌面上,其侧面示意图如图所示,若 , , 则的长为( ) A、 B、 C、 D、5. 下列图形中,线段表示的高线的是( )A、
A、 B、 C、 D、5. 下列图形中,线段表示的高线的是( )A、 B、
B、 C、
C、 D、
D、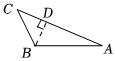 6. 下列命题属于假命题的是( )A、全等三角形的对应边相等 B、全等三角形的对应角相等 C、三条边对应相等的两个三角形全等 D、三个角对应相等的两个三角形全等7. 如图,在中于点 , 为上一点连结交于点 , 若 , , 则与的和为( )
6. 下列命题属于假命题的是( )A、全等三角形的对应边相等 B、全等三角形的对应角相等 C、三条边对应相等的两个三角形全等 D、三个角对应相等的两个三角形全等7. 如图,在中于点 , 为上一点连结交于点 , 若 , , 则与的和为( ) A、 B、 C、 D、8. 如图是两个全等的直角三角形拼成的图形,且点 , , 在同一直线上,连结设 , , 则的面积可以表示为( )
A、 B、 C、 D、8. 如图是两个全等的直角三角形拼成的图形,且点 , , 在同一直线上,连结设 , , 则的面积可以表示为( ) A、 B、 C、 D、9. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( )
A、 B、 C、 D、9. 如图,在等边中,为中点,点 , 分别为 , 上的点, , , 在上有一动点 , 则的最小值为( ) A、7 B、8 C、9 D、1010. 如图,在中, , , 以顶点为圆心,长为半径画弧,交边于点 , 再分别以点 , 为圆心,适当的长度为半径画弧,两弧交于点 , 作射线交边于点 , 点为边上的动点,若 , 则的取值范围是( )
A、7 B、8 C、9 D、1010. 如图,在中, , , 以顶点为圆心,长为半径画弧,交边于点 , 再分别以点 , 为圆心,适当的长度为半径画弧,两弧交于点 , 作射线交边于点 , 点为边上的动点,若 , 则的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
11. 等边三角形的每一个内角均为度.12. 命题“同位角相等,两直线平行”的逆命题是: .13. 李老师在探究等腰三角形“三线合一”性质时,部分板书如图所示,请帮他在横线上填一个适当的结论.
 14. 将两块全等的直角三角板如图放置,其中一块三角板的斜边恰好经过另一块三角板的直角顶点及斜边上的中点 , 若这两块三角板的斜边长为 , 则.
14. 将两块全等的直角三角板如图放置,其中一块三角板的斜边恰好经过另一块三角板的直角顶点及斜边上的中点 , 若这两块三角板的斜边长为 , 则. 15. 在中, , 为边上一点,将三角形沿折叠,使落在边上,点与点重合,若为直角三角形,则的度数为.
15. 在中, , 为边上一点,将三角形沿折叠,使落在边上,点与点重合,若为直角三角形,则的度数为.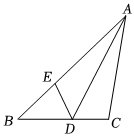 16. 如图,在中, , , , 点为上动点,为上一点,且 , 当点从点运动到点时,则点运动的路程为.
16. 如图,在中, , , , 点为上动点,为上一点,且 , 当点从点运动到点时,则点运动的路程为.
三、解答题(本大题共8小题,共52.0分。)
-
17. 如图,阴影部分是由4个小正方形组成的“”形,请用二种方法分别在如图的空白方格内涂黑一个小正方形,使阴影部分成为轴对称图形.
 18. 如图, , , 求证:.
18. 如图, , , 求证:. 19. 如图,在中,尺规作图保留作图痕迹,不写作法
19. 如图,在中,尺规作图保留作图痕迹,不写作法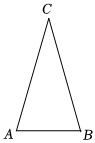
⑴作边的垂直平分线;
⑵在内确定一点 , 使得点到三个顶点的距离相等.
20. 已知的三条边长分别为 , , , 其中 , , , 且是直角三角形吗?请证明你的判断.21. 如图,在中, , , 为上一点,连结 , 作 , 交线段于点. (1)、直接写出 , 的大小;(2)、若 , 求的大小.22. 如图,在中, , , 点是上一点,连结设: , 当分别满足下列条件时,求的值.
(1)、直接写出 , 的大小;(2)、若 , 求的大小.22. 如图,在中, , , 点是上一点,连结设: , 当分别满足下列条件时,求的值. (1)、AD为边上的中线;(2)、AD为的平分线.
(1)、AD为边上的中线;(2)、AD为的平分线.

