2022-2023学年北师大版数学八年级上册期末测试卷2
试卷更新日期:2022-12-13 类型:期末考试
一、单选题(每题3分,共30分)
-
1. 二次根式、、、中最简二次根式有( )A、1个 B、2个 C、3个 D、4个2. 若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是5,则点P的坐标是( )A、 B、 C、 D、3. 若一次函数的图象不经过第三象限,则( )A、 B、 C、 D、4. 利用代入法解方程组将①代入②得( )A、 B、 C、 D、5. 如图,中, , 现将沿进行翻折,使点A刚好落在 , 则的长为( )
 A、 B、 C、2 D、6. 如果与的平均数是5,那与的平均数是( )A、4 B、5 C、6 D、77. 已知点 和 关于 轴对称,则 ( )A、-1 B、1 C、-2 D、28. 如图,在中,D为上一点, , 则的度数为( )
A、 B、 C、2 D、6. 如果与的平均数是5,那与的平均数是( )A、4 B、5 C、6 D、77. 已知点 和 关于 轴对称,则 ( )A、-1 B、1 C、-2 D、28. 如图,在中,D为上一点, , 则的度数为( ) A、 B、 C、 D、9. 甲、乙两人共同解关于x,y的方程组 ,甲符合题意地解得 乙看错了方程②中的系数c,解得 ,则 的值为( )A、16 B、25 C、36 D、4910. 一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车行驶的路程y1(km),小轿车行驶的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( )
A、 B、 C、 D、9. 甲、乙两人共同解关于x,y的方程组 ,甲符合题意地解得 乙看错了方程②中的系数c,解得 ,则 的值为( )A、16 B、25 C、36 D、4910. 一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地,货车行驶的路程y1(km),小轿车行驶的路程y2(km)与时间x(h)的对应关系如图所示,下列结论错误的是( ) A、甲、乙两地相距420km B、y1=60x,y2=
A、甲、乙两地相距420km B、y1=60x,y2=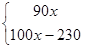 C、货车出发4.5h与小轿车首次相遇
D、两车首次相遇时距乙地150km
C、货车出发4.5h与小轿车首次相遇
D、两车首次相遇时距乙地150km
二、填空题(每空3分,共18分)
-
11. 已知点和关于y轴对称,则= .12. 计算: .13. 甲、乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差S2甲与S2乙的大小关系是S2甲S2乙 . (填“>”或“<”)
 14. 如图,已知直线l1:y=3x+1和直线l1:y=mx+n交于点P(1,b),则关于x,y的二元一次方程组 的解是 .
14. 如图,已知直线l1:y=3x+1和直线l1:y=mx+n交于点P(1,b),则关于x,y的二元一次方程组 的解是 .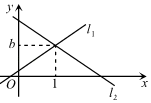 15. 如图,在中, , , 点D在边上,将沿折叠得到 , 若恰有 , 则度.
15. 如图,在中, , , 点D在边上,将沿折叠得到 , 若恰有 , 则度.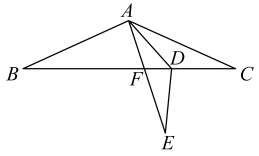 16. 如图,AB⊥BC,CD⊥BC,垂足分别为B,C,P为线段BC上一点,连接PA,PD,已知AB=5,DC=4,BC=12,则AP+DP的最小值为 .
16. 如图,AB⊥BC,CD⊥BC,垂足分别为B,C,P为线段BC上一点,连接PA,PD,已知AB=5,DC=4,BC=12,则AP+DP的最小值为 .
三、计算题(共6分)
-
17. 解方程组(1)、 .(2)、 .
四、解答题(共6题,共46分)
-
18. 如图,△ABC中,已知点A(-1,4),B(-2,2),C(1,1).
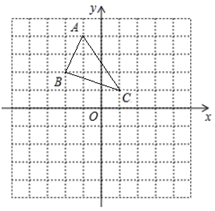 (1)、作ΔABC关于x轴对称的△A1B1C1 , 并写出点A1 , B1 , C1的坐标,(2)、作△ABC关于y轴对称的△A2B2C2 , 并写出点A2 , B2 , C2的坐标,(3)、观察点A1 , B1 , C1和A2 , B2 , C2的坐标,请用文字语言归纳点A1和A2 , B1和B2 , C1和C2坐标之间的关系.19. 我校准备挑选一名跳高运动员参加区中学生运动会,对跳高队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
(1)、作ΔABC关于x轴对称的△A1B1C1 , 并写出点A1 , B1 , C1的坐标,(2)、作△ABC关于y轴对称的△A2B2C2 , 并写出点A2 , B2 , C2的坐标,(3)、观察点A1 , B1 , C1和A2 , B2 , C2的坐标,请用文字语言归纳点A1和A2 , B1和B2 , C1和C2坐标之间的关系.19. 我校准备挑选一名跳高运动员参加区中学生运动会,对跳高队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175
(1)甲、乙两名运动员的跳高平均成绩分别是多少?
(2)哪名运动员的成绩更为稳定?为什么?
(3)若预测,跳过165cm就很可能获得冠军。该校为了获得冠军,可能选哪位运动员参赛?若预测跳过170cm才能得冠军呢?为什么?20. 如图,、相交于点 , , 于点 , 于点 , 且 .求证: .
 21. 新冠肺炎疫情期间,佩戴口罩是做好个人防护的重要举措。小明家先后两次在同一电商平台以相同的单价邮购买了A、B两种型号的口罩,第一次购买20个A型口罩,30个B型口罩,共花费190元;第二次购买30个A型口罩,20个B型口罩,共花费160元,求A、B两种型号口罩的单价.22. 已知,如图,在△ABC中,∠C= 90°,AD平分∠BAC交BC于D,过D作DE∥AC交AB于E.
21. 新冠肺炎疫情期间,佩戴口罩是做好个人防护的重要举措。小明家先后两次在同一电商平台以相同的单价邮购买了A、B两种型号的口罩,第一次购买20个A型口罩,30个B型口罩,共花费190元;第二次购买30个A型口罩,20个B型口罩,共花费160元,求A、B两种型号口罩的单价.22. 已知,如图,在△ABC中,∠C= 90°,AD平分∠BAC交BC于D,过D作DE∥AC交AB于E.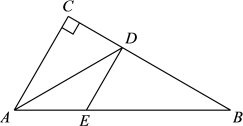 (1)、求证:AE=DE;(2)、如果AC=3, , 求AE的长.23. 为加强独秀山公园的建设,需用甲、乙两种石材.经市场调查,甲种石材的费用y(元)与使用面积间的函数关系如图所示,乙种石材的价格为每平方米70元.
(1)、求证:AE=DE;(2)、如果AC=3, , 求AE的长.23. 为加强独秀山公园的建设,需用甲、乙两种石材.经市场调查,甲种石材的费用y(元)与使用面积间的函数关系如图所示,乙种石材的价格为每平方米70元. (1)、求y与x间的函数表达式;(2)、若公园建设总面积共 , 其中使用甲石材 , 设购买两种石材的总费用为w元,请直接写出w与x间的函数表达式;(3)、在(2)的前提下,若甲种石材使用面积不少于 , 且不超过乙种石材面积的2倍,那么应该怎样分配甲、乙两种石材的面积才能使总费用最少?最少总费用为多少元?
(1)、求y与x间的函数表达式;(2)、若公园建设总面积共 , 其中使用甲石材 , 设购买两种石材的总费用为w元,请直接写出w与x间的函数表达式;(3)、在(2)的前提下,若甲种石材使用面积不少于 , 且不超过乙种石材面积的2倍,那么应该怎样分配甲、乙两种石材的面积才能使总费用最少?最少总费用为多少元?
-