2023年中考数学复习考点一遍过——二次根式
试卷更新日期:2022-12-12 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 使有意义的x的取值范围在数轴上表示为( )A、
 B、
B、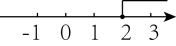 C、
C、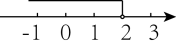 D、
D、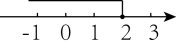 2. 化简的结果是( )A、2 B、3 C、2 D、23. 下列正确的是()A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 若式子在实数范围内有意义,则x的取值范围是( )A、 B、 C、且 D、且6. 下列各式计算正确的是( )A、 B、 C、 D、7. 下列计算正确的是( )A、32=6 B、(﹣)3=﹣ C、(﹣2a2)2=2a4 D、+2=38. 下列计算错误的是( )A、 B、 C、 D、9. 下列运算正确的是( )A、 B、 C、 D、10. 估计 的值应在( )A、10和11之间 B、9和10之间 C、8和9之间 D、7和8之间
2. 化简的结果是( )A、2 B、3 C、2 D、23. 下列正确的是()A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 若式子在实数范围内有意义,则x的取值范围是( )A、 B、 C、且 D、且6. 下列各式计算正确的是( )A、 B、 C、 D、7. 下列计算正确的是( )A、32=6 B、(﹣)3=﹣ C、(﹣2a2)2=2a4 D、+2=38. 下列计算错误的是( )A、 B、 C、 D、9. 下列运算正确的是( )A、 B、 C、 D、10. 估计 的值应在( )A、10和11之间 B、9和10之间 C、8和9之间 D、7和8之间二、填空题(每空3分,共33分)
-
11. 若二次根式在实数范围内有意义,那么x的取值范围是 .12. 若在实数范围内有意义,则实数x的取值范围是 .13. 使式子有意义的的取值范围是.14. 计算的结果是.15. 计算: .16. 计算的结果是 .17. 若(a﹣3)2+=0,则以a、b为边长的等腰三角形的周长为.18. 若实数m,n满足 ,则 .19. 已知m为正整数,若是整数,则根据可知m有最小值.设n为正整数,若是大于1的整数,则n的最小值为 , 最大值为.20. 观察下列各式:
,
,
,
……
请利用你发现的规律,计算:
其结果为
三、计算题(共4题,共30分)
-
21. 计算:(1)、(2)、22. 计算:23. 计算24. 计算:(1)、;(2)、;
四、解答题(共3题,共27分)
-
25. 实数a,b,c在数轴上如图所示,化简:()2﹣+|b﹣c|+ .
 26. 阅读材料:像(+)(﹣)=3,=a(a≥0)、(+1)(﹣1)=b﹣1(b≥0)……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如与 , +1与﹣1,2+3与2﹣3等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
26. 阅读材料:像(+)(﹣)=3,=a(a≥0)、(+1)(﹣1)=b﹣1(b≥0)……两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.例如与 , +1与﹣1,2+3与2﹣3等都是互为有理化因式.在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.例如:; . 解答下列问题:
(1)、3﹣与互为有理化因式,将分母有理化得;(2)、①直接写出式子的计算结果 .
②比大小(直接填>,<,=,≥或≤中的一种)
(3)、已知有理数a、b满足 , 求a、b的值.27. 已知 ,(1)、观察上式得出规律,则 , .(2)、若的值.(3)、由(2)中、的值,求的值.