2023年中考数学复习考点一遍过——分式

试卷更新日期：2022-12-12 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 代数式 $\frac{2}{5}$ x， $\frac{1}{π}$ ， $\frac{2}{x^{2} + 4}$ ， x²﹣ $\frac{2}{3}$ ， $\frac{1}{x}$ ， $\frac{x + 1}{x + 2}$ 中，属于分式的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 在函数y＝ $\frac{\sqrt{x + 3}}{x}$ 中，自变量x的取值范围是（）

A、x≥3 B、x≥﹣3 C、x≥3且x≠0 D、x≥﹣3且x≠0

查看试题解析
3. 若m－n＝2，则代数式 $\frac{m^{2} - n^{2}}{m} \cdot \frac{2 m}{m + n}$ 的值是（）

A、－2 B、2 C、－4 D、4

查看试题解析
4. 据报道：芯片被誉为现代工业的掌上明珠，芯片制造的核心是光刻技术，我国的光刻技术水平已突破到 $28 n m$ .已知 $1 n m = 1 0^{- 9} m$ ，则 $28 n m$ 用科学记数法表示是（）

A、 $28 \times 1 0^{- 9} m$ B、 $2.8 \times 1 0^{- 9} m$ C、 $2.8 \times 1 0^{- 8} m$ D、 $2.8 \times 1 0^{- 10} m$

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{\frac{1}{2}} \times \sqrt{8} = \pm 2$ B、 $(m + n)^{2} = m^{2} + n^{2}$ C、 $\frac{1}{x - 1} - \frac{2}{x} = - \frac{1}{x}$ D、 $3 x y \div \frac{- 2 y^{2}}{3 x} = - \frac{9 x^{2}}{2 y}$

查看试题解析
6. 下列计算错误的是（）

A、 $| - 2 | = 2$ B、 $a^{2} \cdot a^{- 3} = \frac{1}{a}$ C、 $\frac{a^{2} - 1}{a - 1} = a + 1$ D、 ${(a^{2})}^{3} = a^{3}$

查看试题解析
7. 化简 $\frac{1}{a - 3} - \frac{6}{a^{2} - 9}$ 的结果是（）

A、 $\frac{1}{a + 3}$ B、 $a - 3$ C、 $a + 3$ D、 $\frac{1}{a - 3}$

查看试题解析
8. 化简 $\frac{4}{a + 2} + a - 2$ 的结果是（）

A、1 B、 $\frac{a^{2}}{a + 2}$ C、 $\frac{a^{2}}{a^{2} - 4}$ D、 $\frac{a}{a + 2}$

查看试题解析
9. 试卷上一个正确的式子（ $\frac{1}{a + b} + \frac{1}{a - b}$ ）÷★＝ $\frac{2}{a + b}$ 被小颖同学不小心滴上墨汁．被墨汁遮住部分的代数式为（）

A、 $\frac{a}{a - b}$ B、 $\frac{a - b}{a}$ C、 $\frac{a}{a + b}$ D、 $\frac{4 a}{a^{2} - b^{2}}$

查看试题解析
10. 若x是非负整数，则表示 $\frac{2 x}{x + 2} - \frac{x^{2} - 4}{{(x + 2)}^{2}}$ 的值的对应点落在下图数轴上的范围是（）

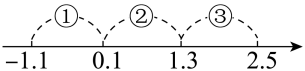A、① B、② C、③ D、①或②

查看试题解析

二、填空题（每题3分，共30分）

11. 当 $x =$ 时，分式 $\frac{2 x}{x + 2}$ 的值为零.

查看试题解析
12. 科学家在实验室中检测出某种病毒的直径的为0.000000103米，该直径用科学记数法表示为米.

查看试题解析
13. 若代数式 $\sqrt{x + 1} + \frac{1}{x}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
14. 计算：|-4|+(3-π)⁰=.

查看试题解析
15. 化简 $\frac{x^{2}}{x - 2} - \frac{2 x}{x - 2}$ 的结果是.

查看试题解析
16. 如图的解题过程中，第①步出现错误，但最后所求的值是正确的，则图中被污染的x的值是．

先化简，再求值： $\frac{3 - x}{x - 4} + 1$ ，其中 $x =$

解：原式 $= \frac{3 - x}{x - 4} \cdot (x - 4) + (x - 4) \dots ①$

$= 3 - x + x - 4$

$= - 1$

查看试题解析
17. 若实数a、b分别满足a²﹣4a+3＝0，b²﹣4b+3＝0，且a≠b，则 $\frac{1}{a} + \frac{1}{b}$ 的值为 .

查看试题解析
18. 化简： $(1 - \frac{1}{x + 1}) \cdot \frac{x^{2} - 1}{x} =$ ．

查看试题解析
19. 若 $a^{2} - 2 a - 15 = 0$ ，则代数式 $(a - \frac{4 a - 4}{a}) \cdot \frac{a^{2}}{a - 2}$ 的值是．

查看试题解析
20. 人们把 $\frac{\sqrt{5} - 1}{2} \approx 0.618$ 这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比.设 $a = \frac{\sqrt{5} - 1}{2}$ ， $b = \frac{\sqrt{5} + 1}{2}$ ，记 $S_{1} = \frac{1}{1 + a} + \frac{1}{1 + b}$ ， $S_{2} = \frac{2}{1 + a^{2}} + \frac{2}{1 + b^{2}}$ ，…， $S_{100} = \frac{100}{1 + a^{100}} + \frac{100}{1 + b^{100}}$ ，则 $S_{1} + S_{2} + \dots + S_{100} =$ .

查看试题解析

三、解答题（共7题，共60分）

21. 计算： $\frac{a^{2} + 2 a}{a} \cdot \frac{a}{a^{2} - 4} - \frac{2}{a - 2}$ ．

查看试题解析
22. 先化简，再求值： $(1 + \frac{2}{a + 1}) \div \frac{a^{2} + 6 a + 9}{a + 1}$ ，从-3，-1，2中选择合适的a的值代入求值．

查看试题解析
23. 先化简，再求值： $\frac{a b}{a - b} \div (\frac{1}{a + b} + \frac{2 b}{a^{2} - b^{2}})$ ，其中 $a = \sqrt{5} + 1$ ， $b = \sqrt{5} - 1$ .

查看试题解析
24. 先化简，再求值： $(a - \frac{4}{a}) \div \frac{a - 2}{a^{2}}$ ，请从不等式组 ${\begin{array}{l} a + 1 > 0 \\ \frac{4 a - 5}{3} \leq 1 \end{array}$ 的整数解中选择一个合适的数求值．

查看试题解析
25. 先化简，简求值： $\frac{x^{2} - 4}{x^{2} - 4 x + 4} \div \frac{x + 3}{x^{2} - 2 x} + \frac{x}{x + 3}$ ，其中 $x = {(\frac{1}{2})}^{- 2}$ ．

查看试题解析
26. 以下是某同学化简分式 $(\frac{x + 1}{x^{2} - 4} - \frac{1}{x + 2}) \div \frac{3}{x - 2}$ 的部分运算过程：
解：原式 $= [\frac{x + 1}{(x + 2) (x - 2)} - \frac{1}{x + 2}] \times \frac{x - 2}{3}$ ①
$= [\frac{x + 1}{(x + 2) (x - 2)} - \frac{x - 2}{(x + 2) (x - 2)}] \times \frac{x - 2}{3}$ ②
$= \frac{x + 1 - x - 2}{(x + 2) (x - 2)} \times \frac{x - 2}{3}$ ③
…
解：

(1)、上面的运算过程中第步出现了错误；

(2)、请你写出完整的解答过程．

查看试题解析
27. 观察下面的等式： $\frac{1}{2} = \frac{1}{3} + \frac{1}{6}$ ， $\frac{1}{3} = \frac{1}{4} + \frac{1}{12}$ ， $\frac{1}{4} = \frac{1}{5} + \frac{1}{20}$ ，……

(1)、按上面的规律归纳出一个一般的结论(用含n的等式表示，n为正整数)．

(2)、请运用分式的有关知识，推理说明这个结论是正确的。

查看试题解析