江苏省盐城市盐都区第一共同体2022-2023学年七年级上学期第三次(12月)自主练习数学试题
试卷更新日期:2022-12-12 类型:月考试卷
一、选择题(本大题共有8小题,每小题3分,共24分。)。
-
1. 下列图形中,能将其中一个图形平移得到另一个图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
2. 在、5、-3π、8.1、1.41414141中,有理数有( )A、1个 B、2个 C、3个 D、4个
-
3. 在方程①3x+y=4,②2x-=5,③3y+2=2-y,④2x2-5x+6=2(x2+3x)中,是一元一次方程的个数为( )A、1个 B、2个 C、3个 D、4个
-
4. 下列各组代数式中,不是同类项的是( )A、2与-5 B、-0.5xy2与3x2y C、-3t与200t D、ab2与-b2a
-
5. 如图是一个正方体纸盒的外表面展开图,则这个正方体( )
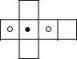 A、
A、 B、
B、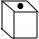 C、
C、 D、
D、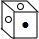
-
6. 古代名著《算学启蒙》中有一题:良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之?意思是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马几天可追上慢马?若设快马x天可追上慢马,则由题意,可列方程为( )A、 B、 C、 D、
-
7.
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
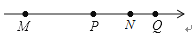 A、点M B、点N C、点P D、点Q
A、点M B、点N C、点P D、点Q -
8. 按如下的方法构造一个多位数:先任意写一个整数n(0<n<10)作为第一位上的数字,将这个整数n乘以3,若积为一位数,则将其作为第2位上的数字,若积为两位数,则将其个位数字作为第2位上的数字;再将第2位上的数字乘以3,若积为一位数,则将其作为第3位上的数字,若积为两位数,则将其个位数字作为第3位上的数字;…以此类推.若先任意写的一个整数n是7作为第一位上的数字,进行2020次如上操作后得到了第2021位上的数字,则第2022位上的数字是( )A、1 B、3 C、7 D、9
二、填空题(本大题共有8小题,每小题3分,共24分。)。
-
9. -2022的相反数是 .
-
10. 人的血管首尾相连的长度大约可达96000千米,96000用科学记数法表示为 .
-
11. 若是关于x的方程的解,则 .
-
12. 若a2-3b=4,则6b-2a2+2018= .
-
13. 若是关于的一元一次方程,则=.
-
14. 若3xm+5y3与x2yn的差仍为单项式,则m+n= .
-
15. “双十一”期间,某电商决定对网上销售的某种服装按成本价提高 40%后标价,又以 8 (即按标价的 80%)优惠卖出,结果每件服装仍可获利 21 元,则这种服装每件的成本是.
-
16. 如图,已知图①是一块边长为1,周长记为C1的等边三角形卡纸,把图①的卡纸剪去一个边长为的等边三角形纸板后得到图②,然后沿同一底边再剪去一个边长为的等边三角形后得到图③,依次剪去一个边长为、、…的等边三角形后,得到图④、⑤、⑥、…,记图n(n≥3)中的卡纸的周长为Cn , 则Cn-Cn-1= .

三、解答题(本大题共有10小题,共72分.)
-
17. 计算:
-
18. 计算:(1)、(6a-b)+5a-2b(2)、(7mn-4)-2(-mn+3)
-
19. 解方程(1)、2(3-x)=-4x+5(2)、=+1.
-
20. 已知A=2x2-4xy+y2 , B=4y2+4x2-6xy.(1)、当x=2,y=-1时,求B-2A的值(先化简,再求值).(2)、若|x-2a|+(y-2)2=0,且B-2A=a,求a的值.
-
21. 已知关于 x 的方程 x-a=2 的解与方程 2(x-1)-5=3a 的解相等,求 x 的值.
-
22. 有这样一道题:已知代数式的值为 , 求代数式的值.
小明的解题过程如下:
原式 , 把式子两边同乘2,得 ,
故原代数式的值为 ,
仿照小明的解题方法,解答下面的问题:
(1)、若 , 则;(2)、已知 , , 求的值. -
23. 卡塔尔世界杯正在火热进行中,在购买足球赛门票时,设购买门票张数为 a(张),现有两种购买方案:方案一:若单位赞助广告费 10000 元,则该单位购买门票的价格为60元(总费用=广告赞助费+门票费).方案二:若购买的门票数不超过 100 张,每张 100 元,若所购门票超过 100 张,则超出部分按八折计算. 解答下列问题:(1)、方案一中,用含 a 的代数式来表示总费用为 . 方案二中,当购买的门票数 a 不超过 100 张时,用含 x 的代数式来表示总费用为 .当所购门票数 a 超过 100 张时,用含 x 的代数式来表示总费用为 .(2)、甲、乙两单位分别采用方案一、方案二购买本次足球赛门票,合计 700 张,花去的总费用计 58000元,求甲、乙两单位各购买门票多少张?
-
24. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
 (1)、小明总共剪开了条棱.(直接写出答案)(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、据小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是88cm,求这个长方体纸盒的体积.
(1)、小明总共剪开了条棱.(直接写出答案)(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、据小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是88cm,求这个长方体纸盒的体积. -
25. 如果两个方程的解相差k,k为正整数,则称解较大的方程为另一个方程的“k—后移方程”.例如:方程是方程的“2—后移方程”.(1)、若方程是方程的“a—后移方程”,则;(2)、若关于x的方程是关于x的方程的“2—后移方程”,求代数式的值:(3)、当时,如果方程是方程的“3—后移方程”,求代数式的值.
-
26. 【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a-b|,线段AB的中点表示的数为 .

【问题情境】如图,数轴上点A表示的数为-2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
【综合运用】
(1)、填空:①A、B两点间的距离AB= , 线段AB的中点表示的数为 ;
②用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)、求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;(3)、求当t为何值时,PQ=AB;(4)、若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
