陕西省西安市高陵区2022-2023学年九年级上学期期中考试数学试题
试卷更新日期:2022-12-12 类型:期中考试
一、选择题(共8小题,每小题3分,计24分.)
-
1. 下列方程中,属于一元二次方程的是( )A、 B、 C、 D、2. 若 , 则的值为( )A、 B、 C、 D、3. 如图,已知 , 若 , 则的值为( )
 A、 B、 C、2 D、4. 某射击运动员在同一条件下射击,结果如下表所示:
A、 B、 C、2 D、4. 某射击运动员在同一条件下射击,结果如下表所示:射击总次数n
10
20
50
100
200
500
1000
击中靶心的次数m
8
17
40
79
158
390
780
击中靶心的频率
0.8
0.85
0.8
0.79
0.79
0.78
0.78
根据频率的稳定性,这名运动员射击一次击中靶心的概率约是( )
A、0.78 B、0.79 C、0.8 D、0.855. 如图,如果 , 那么添加下列一个条件后,仍不能确定的是( ) A、 B、 C、 D、6. 如图,四边形和四边形是两个矩形,点B在边上,若 , 则矩形的面积为( )
A、 B、 C、 D、6. 如图,四边形和四边形是两个矩形,点B在边上,若 , 则矩形的面积为( ) A、3 B、 C、 D、67. 某产品经过两次连续涨价,销售单价由原来的28元上升到40元,若该产品平均每次涨价的百分率为x,根据题意,下列方程正确的是( )A、 B、 C、 D、8. 如图,四边形为菱形,相交于点O,E是的中点,连接并延长交于点F.已知 , 则的长为( )
A、3 B、 C、 D、67. 某产品经过两次连续涨价,销售单价由原来的28元上升到40元,若该产品平均每次涨价的百分率为x,根据题意,下列方程正确的是( )A、 B、 C、 D、8. 如图,四边形为菱形,相交于点O,E是的中点,连接并延长交于点F.已知 , 则的长为( ) A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题(共5小题,每小题3分,计15分)
-
9. 如图,以正方形的中心为原点建立平面直角坐标系,点A的坐标为 , 则点D的坐标为 .
 10. 如图,在边长为1的正方形网格中,点A,B,C,D都在格点处,线段与相交于点E,则的值为 .
10. 如图,在边长为1的正方形网格中,点A,B,C,D都在格点处,线段与相交于点E,则的值为 . 11. 若关于x的一元二次方程有一个根是1,则m的值为 .12. 从甲、乙、丙、丁四名同学中随机选取两名同学去参加“喜迎二十大”的演讲比赛,则恰好抽到乙、丙同学的概率是 .13. 符合黄金分割比例形式的图形很容易使人产生视觉上的美感。在如图所示的五角星中, , 且C,D两点都是的黄金分割点,则的长为 .
11. 若关于x的一元二次方程有一个根是1,则m的值为 .12. 从甲、乙、丙、丁四名同学中随机选取两名同学去参加“喜迎二十大”的演讲比赛,则恰好抽到乙、丙同学的概率是 .13. 符合黄金分割比例形式的图形很容易使人产生视觉上的美感。在如图所示的五角星中, , 且C,D两点都是的黄金分割点,则的长为 .
三、解答题(共13小题,计81分.)
-
14. 解方程: .15. 如图,菱形的两条对角线相交于点O,若 , 求菱形的周长.
 16. 已知关于x的一元二次方程 . 求证:方程总有两个实数根.17. 如图,在中, . 作出点D,使四边形是矩形.(要求:尺规作图,不写作法,保留作图痕迹)
16. 已知关于x的一元二次方程 . 求证:方程总有两个实数根.17. 如图,在中, . 作出点D,使四边形是矩形.(要求:尺规作图,不写作法,保留作图痕迹)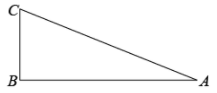 18. 如图,在中, . 求证:是菱形.
18. 如图,在中, . 求证:是菱形. 19. 某校将举办“国学经典”的演讲比赛,九年级通过预赛选出三名男生和两名女生,共5名同学作为推荐人选.(1)、若从中随机选一名同学参加学校比赛,则选中女生的概率为 .(2)、若从中随机选两名同学组成一组选手参加比赛,请用树状图(或列表法)求出恰好选中一名男生和一名女生的概率.20. 如图,在中, , D,E分别为边上的点, , 当时,求的长.
19. 某校将举办“国学经典”的演讲比赛,九年级通过预赛选出三名男生和两名女生,共5名同学作为推荐人选.(1)、若从中随机选一名同学参加学校比赛,则选中女生的概率为 .(2)、若从中随机选两名同学组成一组选手参加比赛,请用树状图(或列表法)求出恰好选中一名男生和一名女生的概率.20. 如图,在中, , D,E分别为边上的点, , 当时,求的长.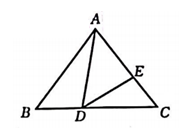 21. 如图,在平行四边形中, , 延长至点E,使 , 连接 .
21. 如图,在平行四边形中, , 延长至点E,使 , 连接 . (1)、求证:四边形是矩形.(2)、连接 , 若 , 求的长.22. 某水果店经销一种进口水果,其进价为每千克40元,按每千克60元的价格出售,每天可售出400千克,市场调查发现,当售价每千克降低1元时,则每天销量可增加50千克.(1)、当售价为每千克50元时,每天销售这种水果千克,每天获得利润元.(2)、若要使每天的利润为9750元,同时又要尽快减少库存,则每千克这种水果应降价多少元?23. 如图,把一个矩形剪去一个边长和它的宽相等的正方形,若剩下的矩形与原矩形相似.
(1)、求证:四边形是矩形.(2)、连接 , 若 , 求的长.22. 某水果店经销一种进口水果,其进价为每千克40元,按每千克60元的价格出售,每天可售出400千克,市场调查发现,当售价每千克降低1元时,则每天销量可增加50千克.(1)、当售价为每千克50元时,每天销售这种水果千克,每天获得利润元.(2)、若要使每天的利润为9750元,同时又要尽快减少库存,则每千克这种水果应降价多少元?23. 如图,把一个矩形剪去一个边长和它的宽相等的正方形,若剩下的矩形与原矩形相似.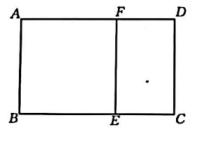 (1)、求原矩形的长和宽的比.(2)、若 , 求矩形的面积.24.(1)、课本再现
(1)、求原矩形的长和宽的比.(2)、若 , 求矩形的面积.24.(1)、课本再现
教材中小颖为学校联欢会设计了一个“配紫色”的游戏,若转盘A转出了红色,转盘B转出了蓝色,就可以配成紫色.小贤和小明受到启发,也制作了两个“配紫色”的游戏转盘(如图1),规则如下:如图,A,B是两个可以自由转动的转盘,两人分别转动两个转盘,若其中一个转盘转出红色,另一个转盘转出蓝色,那么就能配成紫色.若配成紫色,则小贤赢,否则小明赢.这个游戏对双方公平吗?请说明理由. (2)、在(1)中规则不变的情况下,请你在图2中设计一个游戏,使转动两个转盘能配成紫色的概率为 .
(2)、在(1)中规则不变的情况下,请你在图2中设计一个游戏,使转动两个转盘能配成紫色的概率为 .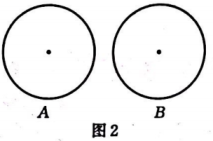 25. 如图1,在纸片中, , D,E分别是边上的动点,且 , 连接 , 将沿翻折,点B落在点F的位置,连接 .
25. 如图1,在纸片中, , D,E分别是边上的动点,且 , 连接 , 将沿翻折,点B落在点F的位置,连接 .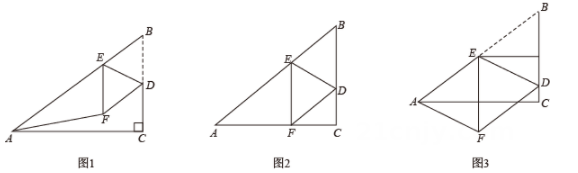 (1)、如图2,当点F在边上时,求的长.(2)、如图3,点D,E在运动过程中,当时,求的长.26. 问题情境
(1)、如图2,当点F在边上时,求的长.(2)、如图3,点D,E在运动过程中,当时,求的长.26. 问题情境在综合实践课上,老师组织兴趣小组开展数学活动,探究正方形的旋转问题.在正方形和正方形中,点G,A,B在一条直线上,连接(如图1).
 (1)、操作发现
(1)、操作发现
图1中线段和的数量关系是 , 位置关系是 .(2)、在图1的基础上,将正方形绕着点A沿顺时针方向旋转,如图2所示,(1)中的结论是否成立?请仅就图2的情况说明理由.(3)、类比探究
如图3,若将图2中的正方形和正方形都变为矩形,且 , 请仅就图3的情况探究与之间的数量关系.