浙江省宁波市慈溪市2022-2023学年八年级上学期期中数学试卷
试卷更新日期：2022-12-12 类型：期中考试
一、选择题（每题3分，共30分）.
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知∠A=37°，∠B=53°，则△ABC为（ ）A、锐角三角形 B、钝角三角形 C、直角三角形 D、以上都有可能3. 等腰三角形的两边长分别为3和6，则这个等腰三角形的周长为( )A、12 B、15 C、12或15 D、184. 下列哪个数是不等式2（x-1）+3＜0的一个解（ ）A、2 B、 C、- D、-35. 能说明命题“对于任何实数a，都有|a|＝a”是假命题的反例是（ ）A、a＝-2 B、 C、a＝1 D、6. 如图，用尺规作出∠AOB的角厉分线OE，在作角平分线过程中，用到的三角形全等的判定方迲是（ ）
A、ASA B、AAS C、SAS D、SSS7. 如图，在△ABC中，AB＝AC，AD是高线，E是AB的中点，已知△ABC的面积为8，则△ADE的面积为（ ）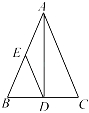
A、1 B、2 C、3 D、48. 如图，Rt△ABC中，∠ACB＝90°，∠A＝20°，△ABC≌△A′B′C′，若A′B′恰好经过点B，A′C′交AB于D，则∠BDC的度数为（ ）
A、50° B、60° C、62° D、64°9. 若不等式组 有解，则m的取值范围是（ ）A、m＜2 B、m≥2 C、m＜1 D、1≤m＜210. 如图1，以直角三角形的各边分别向外作正方形，再把较小的两个正方形按图2的方式放置在大正方形内，记四边形ABCD的面积为S1 ， 四边形DCEG的面积为S2.四边形HGFP的面积为S3 ， △GEF面积为S4 ， 若知道图中阴影部分的面积，则一定能求出（ ）
A、S1 B、S2 C、S3 D、S4二、填空题（每小题4分，共24分）
-
11. “x的2倍与3的差是非负数．”用不等式表示为： ．12. 命题“如果ab＝0，则a＝0”的逆命题是 ．13. 在Rt△ABC中，∠B＝90°，AB＝4，BC＝8，D、E分别是边AC、BC上的点，将△ABC沿着DE进行翻折，点A和点C重合，则EC＝.
14. 若不等式组 的解集为﹣1＜x＜1，那么（a+1）（b﹣1）的值等于 ．15. 如图，在四边形ABCD中，AD∥BC，DE⊥BC，垂足为点E，连接AC交DE于点F，点G为AF的中点，∠ACD＝2∠ACB.若DG＝4，EC＝1，则DE的长为.
16. 如图，在Rt△ABC中，∠A＝90°，AB＝12，AC＝5，M、N、P分别是边AB、AC、BC上的动点，连接PM、PN和MN，则PM+PN+MN的最小值是 .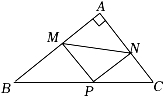
三、解答题.（第17、18题各6分，第19、20、21、22题各8分，第23题10分，第24题12分，共66分）
-
17. 解下列不等式（组）(1)、求不等式的解2（3x+2）-2x＜0；(2)、解不等式组 .18. 如图
(1)、在图1中，用尺规作AB边的中垂线，交BC于点P.（保留作图痕迹）(2)、如图2，是由边长为1的小正方形拼成的网格，画一个以格点为顶点，斜边长为 的直角三角形（各边均为无理数）.19. 如图，在三角形ABC中，AB＝AC，∠C＝25°，点D在线段CA的延长线上，且DA＝AC，求∠ABD的度数.
20. 如图所示，已知△ABD≌△CFD，AD⊥BC于D.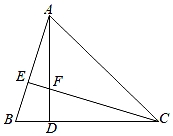
(1)、求证：CE⊥AB；(2)、已知BC＝7，AD＝5，求AF的长.21. 如图已知：E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D.求证：
(1)、∠ECD＝∠EDC；(2)、OE是CD的垂直平分线.22. “低碳生活，绿色出行”已逐渐被大多数人所接受，某自行车专卖店有A，B两种规格的自行车，A型车的利润为a元/辆，B型车的利润为b元/辆，该专卖店十月份前两周销售情况如表：A型车销售量（辆）
B型车销售量（辆）
总利润（元）
第一周
10
12
2240
第二周
20
15
3400
(1)、求a，b的值；(2)、若第三周售出A，B两种规格自行车共25辆，其中B型车的销售量大于A型车的售量，且不超过A型车销售量的1.5倍，该专卖店售出A型、B型车各多少辆才能使第三周利润最大，最大利润是多少元？23. 如图，AO⊥OM，OA＝8，点B为射线OM上的一个动点，分别以OB，AB为直角边，B为直角顶点，在OM两侧作等腰Rt△OBF、等腰Rt△ABE.
(1)、连接AF、OE，求证AF＝OE；(2)、连接EF交OM于P点，当点B在射线OM上移动时，PB的长度的会变化吗？若会变化，请说明理由；若不变，请求出PB的长度.24. 定义：若连结三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形，我们称这条线段为该三角形的智慧线，这个三角形叫做智慧三角形.
(1)、如图1，在智慧三角形ABC中，AD⊥BC，AD为该三角形的智慧线，CD＝1，AC＝2，则BD长为 ， ∠B的度数为.(2)、如图2，△ABC为等腰直角三角形，∠BAC＝90°，F是斜边BC延长线上一点，连结AF，以AF为直角边作等腰直角三角形AFE（点A，F，E按顺时针排列），∠EAF＝90°，AE交BC于点D，连结EC，EB.当∠BDE＝2∠BCE时，求证：ED是△EBC的智慧线.(3)、如图3，△ABC中，AB＝AC＝5，BC2＝80.若△BCD是智慧三角形，且AC为智慧线，求△BCD的面积.