浙江省金华市东阳市2022-2023学年八年级上学期期中数学试卷
试卷更新日期：2022-12-12 类型：期中考试
一、选择题（本题有10小题，每小题3分，共30分.）
-
1. 下面四个图标中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列长度的三条线段不能组成三角形的是（ ）A、1，1，2 B、2，3，4 C、3，4，5 D、3，4，63. 等腰三角形的底角等于50°，则这个等腰三角形顶角的度数是（ ）A、50° B、65° C、80° D、100°4. 下列命题中，逆命题是真命题的是（ ）A、两直线平行，内错角相等 B、若a＝b，那么a2＝b2 C、对顶角相等 D、若a＝b，那么|a|＝|b|5. 如图，在△ABC中，作BC边上的高线，下列画法正确的是（ ）A、
B、
C、
D、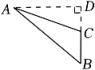
6. 如图，AB⊥CD，垂足为O.添加下列一组条件后，不能判定Rt△AOC≌Rt△BOD的是（ ）
A、AC＝BD，OA＝OB B、OA＝OD，∠A＝∠B C、AC＝BD，OC＝OD D、AC＝BD，AC∥BD7. 如图，在△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE于点E，AD⊥CE于点D.DE＝5，AD＝9，则BE的长是（ ）
A、6 B、5 C、4.5 D、48. 如图，在四边形ABCD中，连结AC，BD，若△ABC是等边三角形，AB＝BD，∠ABD＝20°，则∠BDC的度数为（ ）
A、50° B、60° C、70° D、75°9. 数形结合是数学的重要思想和解题方法，如：“当0＜x＜12时，求代数式 的最小值”，其中 可看作两直角边分别为x和2的Rt△ACP的斜边长， 可看作两直角边分别是12-x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值，如图所示，当AP与BP共线时，AP+BP为最小.请你解决问题：当0＜x＜4时，则代数式 的最小值是（ ）
A、4 B、5 C、6 D、710. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G，连结BG，若大正方形的面积是小正方形面积的5倍，则 的值为（ ）
A、 B、3 C、 D、4二、填空题（本题有8小题，每小题3分，共24分）
-
11. 在△ABC中，∠C＝90°，∠B＝25°，则∠A＝度.12. 在说明命题“若|a|＞3，则a＞3”是假命题的反例中，a的值可以是 .13. 如图，AC＝BD，若要证明△ABC≌△DCB，需要补充的一个条件，可以是 （写出一个即可）.
14. 边长为2cm的等边三角形的面积为cm215. 如图，在△ABC中，∠ACB＝90°，D为AB的中点，AC＝6，BC＝8，则CD＝.
16. 如图，在长方形ABCD中，BC＝4，CD＝2，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，则线段AE的长为 .
17. 如图，梯形ABCD中，∠ABC＝∠BCD，AD∥BC，BD平分∠ABC，若AD＝3，BC＝7，则BD的长为 .
18. 如图1是吊车的实物图，图2是吊车工作示意图，车顶BM与车身CN平行于地面，已知BM到地面的距离为2米，AD＝4.8米，∠MBC＝3∠BCN.吊车作业时是通过液压杆CD的伸缩使起重臂AB绕点B转动的，从而使得起重臂升降作业.在某次起重作业中，学习兴趣小组经过测量发现：液压杆CD为2米时，∠DCN＝120°，∠MBD＝150°，则∠CBD＝度，此时点A到地面的距离为 米.
三、解答题（本题有6小题，共46分.）
-
19. 如图，C为∠AOB平分线上一点，点D在射线OA上，且OD＝CD.
求证：CD∥OB.
20. 如图，在△ABC与△DCB中，已知∠ABD＝∠DCE，∠DBC＝∠ACB.求证：AC＝DB.
21. 如图，在3×6的方格纸中，已知格点P和线段AB.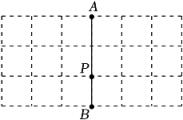
⑴画一个锐角三角形（顶点均在格点上且不与点A，B重合），使P为其中一边的中点.
⑵再画出该三角形关于直线AB对称的图形.
22. 如图，△ABC和△ADE关于直线MN对称，BC与DE的交点F在直线MN上.
(1)、若∠BAC＝100°，∠CAD＝30°，求∠EAF的度数.(2)、若BC∥AD，AE平分∠BAM，∠BFE+∠C＝81°，求∠EAF的度数.
