浙江省宁波市镇海区镇海蛟川书院2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-12 类型:期中考试
一、单选题
-
1. 已知 , 则 ( )A、 B、 C、 D、2. 已知的半径是6cm,点P到圆心O的距离为4,则点P与的位置关系是( )A、点在圆外 B、点在圆上 C、点在圆内 D、无法判断3. 把抛物线 向上平移 个单位,得到的抛物线是( )A、 B、 C、 D、4. 掷一枚质地均匀的标有1,2,3,4,5,6六个数字的立方体骰子,骰子停止后,出现可能性最小的是( )A、大于3的点数 B、小于3的点数 C、大于5的点数 D、小于5的点数5. 如图, 在正五边形中, 是对角线, 交于点 , 则的度数为( )
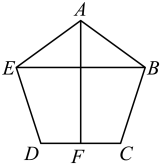 A、 B、 C、 D、6. 如图所示,在△ABC中,D、E为AB、AC的中点,若 , 则四边形DBCE的面积为( )
A、 B、 C、 D、6. 如图所示,在△ABC中,D、E为AB、AC的中点,若 , 则四边形DBCE的面积为( ) A、4 B、6 C、8 D、107. 如图,在正方形网格中,△ABC绕某点旋转一定的角度得到 , 则旋转中心是点( )
A、4 B、6 C、8 D、107. 如图,在正方形网格中,△ABC绕某点旋转一定的角度得到 , 则旋转中心是点( ) A、O B、P C、Q D、M8. 如图示,已知 , 那么添加下列一个条件后,仍无法判定的是( )
A、O B、P C、Q D、M8. 如图示,已知 , 那么添加下列一个条件后,仍无法判定的是( )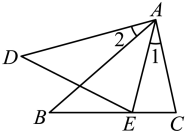 A、 B、 C、 D、9. 如图,是半圆的直径,的平分线分别交弦和半圆于E和D,若 , , 则长为( )
A、 B、 C、 D、9. 如图,是半圆的直径,的平分线分别交弦和半圆于E和D,若 , , 则长为( ) A、2 B、 C、 D、10. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )
A、2 B、 C、 D、10. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )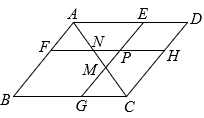 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 抛物线的对称轴是.12. 已知线段 , , 那么线段a、b的比例中项等于cm.13. 在半径为1的圆中,长度等于的弦所对的圆周角是度14. 如图, 等边的边长为2 ,点分别是、、边上的中点,以D为圆心,长为半径作 , 连接.假设可以在内部随机取点, 那么这个点取在阴影部分的概率是.
 15. 如图, 在平行四边形中, 点E是边上一点,连接交于点F, 若 , , , 则的长是.
15. 如图, 在平行四边形中, 点E是边上一点,连接交于点F, 若 , , , 则的长是. 16. 如图, 等腰内接于 , , , 点D是上一点, 连接 , 点E是上一点,满足. 若 , 则的面积是.
16. 如图, 等腰内接于 , , , 点D是上一点, 连接 , 点E是上一点,满足. 若 , 则的面积是.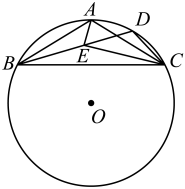
三、解答题
-
17. 图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,点A、B、C、D均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写画法,要求保留必要的作图痕迹.
 (1)、在图①中以线段 为边画一个三角形,使它与 相似.(2)、在图②中画一个三角形,使它与 相似(不全等).(3)、在图③中的线段 上画一个点P,使 .18. 公元前138年张骞出使西域,自长安出发,经匈奴,西行至大宛,经康居,抵达大月氏,再至大夏,最后于公元前126年返回汉朝.张骞出使西域后汉夷文化交往频繁,中原文明通过“丝绸之路”迅速向四周传播.根据古今地图对比,南南同学发现丝绸之路途经现代西安,吐鲁番,喀什等地.(1)、南南爸爸想趁暑假一家人一起出游,若只能去一个地方游览,且选择三个地方的概率相等,那么南南从西安,吐鲁番,喀什三个城市中选择西安的概率是.(2)、若时间充足,南南一家决定以上三个城市都去一趟,求南南一家最后一站去喀什的概率.19. 某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系: , 设这种健身球每天的销售利润为w元.(1)、如果销售单价定为25元,那么健身球每天的销售量是个;(2)、求w与x之间的函数关系式;(3)、该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?20. 如图, 的半径为2,四边形 内接于 ,圆心 到 的距离等于 .
(1)、在图①中以线段 为边画一个三角形,使它与 相似.(2)、在图②中画一个三角形,使它与 相似(不全等).(3)、在图③中的线段 上画一个点P,使 .18. 公元前138年张骞出使西域,自长安出发,经匈奴,西行至大宛,经康居,抵达大月氏,再至大夏,最后于公元前126年返回汉朝.张骞出使西域后汉夷文化交往频繁,中原文明通过“丝绸之路”迅速向四周传播.根据古今地图对比,南南同学发现丝绸之路途经现代西安,吐鲁番,喀什等地.(1)、南南爸爸想趁暑假一家人一起出游,若只能去一个地方游览,且选择三个地方的概率相等,那么南南从西安,吐鲁番,喀什三个城市中选择西安的概率是.(2)、若时间充足,南南一家决定以上三个城市都去一趟,求南南一家最后一站去喀什的概率.19. 某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系: , 设这种健身球每天的销售利润为w元.(1)、如果销售单价定为25元,那么健身球每天的销售量是个;(2)、求w与x之间的函数关系式;(3)、该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?20. 如图, 的半径为2,四边形 内接于 ,圆心 到 的距离等于 . (1)、求 的长;(2)、求 的度数.21. 二次函数的部分图象如图, 其中图象与x轴交于点 , 与 y轴交于点 , 且经过点.
(1)、求 的长;(2)、求 的度数.21. 二次函数的部分图象如图, 其中图象与x轴交于点 , 与 y轴交于点 , 且经过点. (1)、求此二次函数的解析式(2)、图象过三点 , 比较的大小.(用 <连接)(3)、直接写出不等式的解集;22. 学习了相似三角形相关知识后,小明和同学们想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,他的同学在点B处竖立“标杆”AB , 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高EF=1.5米,“标杆”AB=2.5米,又BD=23米,FB=2米.
(1)、求此二次函数的解析式(2)、图象过三点 , 比较的大小.(用 <连接)(3)、直接写出不等式的解集;22. 学习了相似三角形相关知识后,小明和同学们想利用“标杆”测量大楼的高度.如图,小明站立在地面点F处,他的同学在点B处竖立“标杆”AB , 使得小明的头顶点E、杆顶点A、楼顶点C在一条直线上(点F、B、D也在一条直线上).已知小明的身高EF=1.5米,“标杆”AB=2.5米,又BD=23米,FB=2米. (1)、求大楼的高度CD为多少米(CD垂直地面BD)?(2)、小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼CD上点G的高度GD=11.5米,那么相对于第一次测量,标杆AB应该向大楼方向移动多少米?
(1)、求大楼的高度CD为多少米(CD垂直地面BD)?(2)、小明站在原来的位置,同学们通过移动标杆,可以用同样的方法测得楼CD上点G的高度GD=11.5米,那么相对于第一次测量,标杆AB应该向大楼方向移动多少米?

