浙江省杭州市西湖区十三中教育集团（总校）2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-12 类型：期中考试

进入出卷网下载

一、单选题

1. 已知平面内圆的半径为5cm，一点到圆心的距离是3cm，则这点在（）

A、圆外 B、圆上 C、圆内 D、不能确定

查看试题解析
2. 下列事件中属于必然事件的是（）

A、正数大于负数 B、下周二，温州的天气是阴天 C、在一个只装有白球的袋子中摸出一个红球 D、在一张纸上任意画两条线段，这两条线段相交

查看试题解析
3. 二次函数 $y = (x - 2) (x + 3)$ 图象的对称轴是（）

A、直线 $x = 2$ B、直线 $x = - 3$ C、直线 $x = \frac{1}{2}$ D、直线 $x = - \frac{1}{2}$

查看试题解析
4. 下列命题中，正确的是（）

A、圆心角相等，所对的弦相等 B、三点确定一个圆 C、长度相等的弧是等弧 D、弦的垂直平分线必经过圆心

查看试题解析
5. 二次函数 $y = x^{2} - 2 x + 3$ 的图象与坐标轴的交点个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
6. 如图，在 $⊙ O$ 中， $A B$ 是 $⊙ O$ 直径，弦 $C D ⊥ A B$ 于点H.若 $A H = 5$ ， $H B = 1$ ，则 $C D$ 的长为（　　）

A、 $\sqrt{5}$ B、 $\sqrt{13}$ C、 $2 \sqrt{5}$ D、 $2 \sqrt{13}$

查看试题解析
7. 抛物线 $y = a x^{2} + b x - c$ 上部分的横坐标x，纵坐标y的对应值如下表：
x
…
1
2
3
4
y
…
0
$- 1$
0
3
由上表可知，下列结论正确的有（）
① $a < 0$ ；②抛物线与y轴的交点坐标为 $(0 ， 3)$ ；③抛物线的对称轴是直线 $x = 2$ ；④当 $x < 1$ 时，y随x增大而减小；⑤当 $y > 0$ ，则x的取值范围是 $1 < x < 3$ .

A、①④⑤ B、②③⑤ C、②③④ D、①②③

查看试题解析
8. 如图，已知 $A B$ 是 $⊙ O$ 的直径，弦 $C D$ 与 $A B$ 交于点 $E$ ，设 $∠ A B C = a$ ， $∠ A B D = β$ ， $∠ A E C = γ$ ，则（）

A、 $β + γ - α = 90 °$ B、 $α + γ - β = 90 °$ C、 $α + β - γ = 90 °$ D、 $α + β + γ = 180 °$

查看试题解析
9. 规定 $m a x {a ， b} = {\begin{array}{l} a (a \geq b) \\ b (a \leq b) \end{array}$ ，若函数 $y = m a x {- 2 x + 1 ， x^{2} - 2 x - 3}$ ，则该函数的最小值为（）

A、 $- 3$ B、 $- 2$ C、2 D、5

查看试题解析
10. 如图，正方形 $A B C D$ 的边长为6，将长为 $4 \sqrt{3}$ 的线段 $Q F$ 的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发，在 $A B$ 上滑动，同时点F在 $B C$ 上滑动，当点F到达点C时，运动停止，那么在这个过程中，线段 $Q F$ 的中点M所经过的路线长为（）

A、 $π$ B、 $\frac{\sqrt{3}}{3} π$ C、 $\sqrt{6}$ D、 $3 \sqrt{2} - \sqrt{6}$

查看试题解析

二、填空题

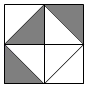
11. 如图是由8块全等的等腰直角三角形黑白瓷砖镶嵌而成的正方形，一只蚂蚁在上面自由爬动，那么蚂蚁停留在黑色瓷砖上的概率是.

查看试题解析
12. 将二次函数 $y = 3 x^{2}$ 的图象先向左平移2个单位，再向上平移4个单位后，得到的抛物线的表达式为.

查看试题解析
13. 如图为《北京2022年冬残奥会会徽》纪念邮票，其规格为边长14.92毫米的正八边形，则正八边形的内角和为.

查看试题解析
14. 二次函数 $y = - x^{2} + 2 x - 3$ .当 $0 \leq x \leq 3$ ，函数值y的最大值为，最小值为.

查看试题解析
15. 在等边 $△ A B C$ 中，以 $B C$ 边的中点O为圆心， $\frac{1}{2} B C$ 长为半径画圆，分别交 $A B ， A C$ 边，于点D，E；P是圆上一动点（与点D、E不重合），连接 $P D ， P E$ ，则 $∠ D P E =$ .

查看试题解析
16. 已知点 $A (m - 2 ， y_{1})$ 、 $B (m ， y_{2})$ 、 $C (x_{0} ， y_{0})$ 在二次函数 $y = a x^{2} - 6 a x + c (a \neq 0)$ 的图象上，且C为抛物线的顶点.

(1)、若 $y_{1} = y_{2}$ ，则m的值是.

(2)、若 $y_{0} \geq y_{1} > y_{2}$ ，则m的取值范围是.

查看试题解析

三、解答题

17. 已知二次函数 $y = a x^{2} - 6 a x + 2$ 的图象经过点 $(- 1 ， 9)$ .

(1)、求此二次函数的表达式；

(2)、求出该抛物线的顶点坐标，并指出当x为何值时y随x的增大而减小.

查看试题解析
18. 在如图所示的方格纸中建立平面直角坐标系，小正方形的边长为1， $△ A B C$ 的三个顶点都在格点上.

(1)、绕点B顺时针旋转 $△ A B C$ ，使得点A落在x轴正半轴上，旋转后的三角形为 $△ A_{1} B C_{1}$ ，画出旋转后的 $△ A_{1} B C_{1}$ ；

(2)、在（1）的条件下，线段 $A B$ 所扫过的面积是.

查看试题解析

19. 有一个圆形转盘，分黑色、白色两个区域.

(1)、某人转动转盘，对指针落在黑色区域或白色区域进行了大量试验，得到数据如下表：

实验次数 $n$ (次)	10	100	2000	5000	10000	50000	100000
白色区域次数 $m$ (次)	3	34	680	1600	3405	16500	33000
落在白色区域频率 $\frac{m}{n}$	0.3	0.34	0.34	0.32	0.34	0.33	0.33

请你利用上述实验，估计转动该转盘指针落在白色区域的概率为.(精确到0.01)；

(2)、若该圆形转盘白色扇形的圆心角为120度，黑色扇形的圆心角为

240 °

，转动转盘两次，求指针一次落在白色区域，另一次落在黑色区域的概率.

查看试题解析

20. 如图，在锐角三角形 $A B C$ 中， $A B = B C$ ，以 $B C$ 为直径作 $⊙ O$ ，分别交 $A B ， A C$ 于点D，E.

(1)、求证： $\overset{⌢}{C E} = \overset{⌢}{D E}$ ；

(2)、若 $∠ A B C = 45 °$ ， $B O = r$ ，求线段 $A D$ 的长（用含r的代数式表示）.

查看试题解析
21. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用 $30 m$ 长的篱笆围成一个矩形花园 $A B C D$ （篱笆只围 $A B 、 B C$ 两边），设 $A B = x$ 米.

(1)、求花园的面积S与x的函数关系式；

(2)、在P处有一棵树与墙 $C D 、 A D$ 的距离分别是 $16 m$ 和 $6 m$ ，要将这棵树围在花园内；（含边界，不考虑树的粗细）
①若花园的面积为 $216 m^{2}$ ，求x的值；
②求花园面积S的最大值.

查看试题解析
22. 已知y关于x的二次函数 $y = x^{2} - 2 m x + 2 m + 4$ ，点P为抛物线顶点.

(1)、若抛物线与y轴的交点坐标为点 $(0 ， 2)$ ，求该二次函数的表达式；

(2)、当P点的纵坐标取最大值时， $m =$ ，此时P点坐标为；

(3)、在（2）的条件下，当 $n - 3 \leq x \leq n$ ，函数有最小值9，求n的值.

查看试题解析
23. 如图，AB为 $⊙ O$ 的直径，点C为AB上方 $⊙ O$ 上一点且 $∠ C A B = 30 °$ ，点D为AB下方 $⊙ O$ 上一点，点E为AD上一点， $∠ B O E = ∠ C A D$ ，连接BC，CD，BD.

(1)、求证： $∠ A O E = ∠ C B D$ ；

(2)、求证： $O E = B D$ ；

(3)、连接CE，若 $C E ⊥ A D$ ， $B D = 4$ ，求半径的长.

查看试题解析

x	…	1	2	3	4
y	…	0	$- 1$	0	3