2023年中考数学复习考点一遍过——因式分解

试卷更新日期：2022-12-11 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下面各式从左到右的变形，属于因式分解的是（）

A、 $x^{2} - x - 1 = x (x - 1) - 1$ B、 $x^{2} - 1 = (x - 1)^{2}$ C、 $x^{2} - x - 6 = (x - 3) (x + 2)$ D、 $x (x - 1) = x^{2} - x$

查看试题解析
2. 把多项式 $a^{2} + 2 a$ 分解因式得（）

A、 $a (a + 2)$ B、 $a (a - 2)$ C、 ${(a + 2)}^{2}$ D、 $(a + 2) (a - 2)$

查看试题解析
3. 下列因式分解正确的是（）

A、 $a x + a y = a (x + y) + 1$ B、 $3 a + 3 b = 3 (a + b)$ C、 $a^{2} + 4 a + 4 = {(a + 4)}^{2}$ D、 $a^{2} + b = a (a + b)$

查看试题解析
4. 下列各式从左到右变形是因式分解，并分解正确的是（）

A、 $(a - b)^{2} + (a - b) = (a - b) (a - b + 1)$ B、 $(x + 2) (x + 3) = x^{2} + 5 x + 6$ C、 $4 a^{2} - b^{2} = (4 a - b) (4 a + b)$ D、 $m^{2} - n^{2} + 2 m n = {(m - n)}^{2}$

查看试题解析
5. 多项式 $x^{2} ﹣ 4 x + 4$ 因式分解的结果是（）

A、x（x﹣4）+4 B、（x+2）（x﹣2） C、（x+2）² D、（x﹣2）²

查看试题解析
6. 多项式 $39 x^{2} + 5 x - 14$ 可因式分解成 $(3 x + a) (b x + c)$ ，其中 $a$ 、 $b$ 、 $c$ 均为整数，求 $a + 2 c$ 之值为何？（）

A、-12 B、-3 C、3 D、12

查看试题解析
7. 如下图，边长为 $a$ 、 $b$ 的长方形周长为16，面积为12，则 $a^{2} b + a b^{2}$ 的值为（）

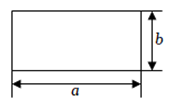A、28 B、96 C、192 D、200

查看试题解析
8. 已知多项式 $2 x^{3} - x^{2} + m$ 分解因式后有一个因式是 $x + 1$ ，则 $m$ 的值为（）

A、3 B、-3 C、1 D、-1

查看试题解析
9. 如图，边长为a、b的长方形周长为20，面积为16，则a²b+ab²的值为（）

A、80 B、160 C、320 D、480

查看试题解析
10. 利用因式分解计算：3²⁰²²﹣3²⁰²¹的结果为（）

A、2×3²⁰²¹ B、1 C、3 D、3²⁰²¹

查看试题解析

二、填空题（每题3分，共30分）

11. 分解因式： $3 a^{2} - 21 a b =$

查看试题解析
12. 因式分解： $3 x^{3} - 12 x y^{2} =$ ．

查看试题解析
13. 分解因式： $a y^{2} + 6 a y + 9 a =$ ．

查看试题解析
14. 因式分解： $a^{2} + 4 a + 4 =$ ．

查看试题解析
15. 分解因式： $x^{2} y - 2 x y^{2} + y^{3} =$ ．

查看试题解析
16. 分解因式：a⁴﹣3a²﹣4＝.

查看试题解析
17. 分解因式： $2022 x^{2} - 4044 x + 2022 =$ .

查看试题解析
18. 因式分解： ${(m + n)}^{2} - 6 (m + n) + 9 =$ ．

查看试题解析
19. 已知m，n同时满足2m+n＝3与2m﹣n＝1，则4m²﹣n²的值是．

查看试题解析
20. 已知 $m^{2} + n^{2} + 10 = 6 m - 2 n$ ，则 $m - n =$ .

查看试题解析

三、解答题（共8题，共60分）

21. 在三个整式 $x^{2} + 4 x y$ ， $y^{2} - 2 x y$ ， $x^{2}$ 中，请你任意选出两个进行加（或减）运算，使所得整式可以因式分解，并进行因式分解．

查看试题解析
22. 已知 $a ， b 、 c$ 是 $△ A B C$ 的三边的长，若满足 $(a - b) b - (b - a) c = 0$ ，试判断此三角形的形状.

查看试题解析
23. 甲、乙两个同学因式分解 $x^{2} + a x + b$ 时，甲看错了a，分解结果为 $(x + 4) (x - 8)$ ，乙看错了b，分解结果为 $(x - 2) (x + 6)$ ．求多项式 $x^{2} + a x + b$ 分解因式的正确结果．

查看试题解析
24. 阅读下面例题，并解答问题。
例题：已知二次三项式 $x^{2} - 4 x + m$ 有一个因式是 $(x + 3)$ ，求另一个因式以及m的值

解：设另一个因式为 $(x + n)$ ，得 $x^{2} - 4 x + m = (x + 3) (x + n)$

则 $x^{2} - 4 x + m = x^{2} + (n + 3) x + 3 n$ ∴ ${\begin{cases} n + 3 = - 4 \\ m = 3 n \end{cases}$ 解得： $n = - 7$ ， $m = - 21$

∴另一个因式为 $(x - 7)$ ，m的值为—21

请仿照上面的方法解答下面的问题：

已知二次三项式 $2 x^{2} + 3 x - k$ 有一个因式是 $(x - 5)$ ，求另一个因式以及k的值。

查看试题解析
25. 已知 $A = a + 2 ， B = a^{2} + a - 7$ ，其中 $a > 2$ ，求出 $A$ 与 $B$ 哪个大.

查看试题解析
26. 试说明对于任意自然数n，代数式n（n+7）-n（n-5）+6的值都能被6整除。

查看试题解析
27. 如图，学校劳动实践基地有两块边长分别为 $a$ ， $b$ 的正方形秧田 $A$ ， $B$ ，其中不能使用的面积为 $M$ ．

(1)、用含 $a$ ， $M$ 的代数式表示 $A$ 中能使用的面积；

(2)、若 $a + b = 10$ ， $a - b = 5$ ，求 $A$ 比 $B$ 多出的使用面积．

查看试题解析
28. 八年级课外兴趣小组活动时，老师提出了如下问题：
将 $2 a - 3 a b - 4 + 6 b$ 因式分解．
【观察】经过小组合作交流，小明得到了如下的解决方法：
解法一：原式 $= (2 a - 3 a b) - (4 - 6 b) = a (2 - 3 b) - 2 (2 - 3 b) = (2 - 3 b) (a - 2)$
解法二：原式 $= (2 a - 4) - (3 a b - 6 b) = 2 (a - 2) - 3 b (a - 2) = (a - 2) (2 - 3 b)$
【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．（温馨提示：因式分解一定要分解到不能再分解为止）

(1)、【类比】
请用分组分解法将 $x^{2} - a^{2} + x + a$ 因式分解；

(2)、【挑战】
请用分组分解法将 $a x + a^{2} - 2 a b - b x + b^{2}$ 因式分解；

(3)、【应用】
“赵爽弦图”是我国古代数学的骄傲，我们利用它验证了勾股定理．如图，“赵爽弦图”是由四个全等的直角三角形围成的一个大正方形，中间是一个小正方形．若直角三角形的两条直角边长分别是a和 $b (a > b)$ ，斜边长是3，小正方形的面积是1．根据以上信息，先将 $a^{4} - 2 a^{3} b + 2 a^{2} b^{2} - 2 a b^{3} + b^{4}$ 因式分解，再求值．

查看试题解析