2023年中考数学复习考点一遍过——整式

试卷更新日期：2022-12-11 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列运算中，结果正确的是（）

A、 $3 a^{2} + 2 a^{2} = 5 a^{4}$ B、 $a^{3} - 2 a^{3} = a^{3}$ C、 $a^{2} \cdot a^{3} = a^{5}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
2. 下列各式运算正确的是（）

A、 $- 3 (x - y) = - 3 x + y$ B、 $x^{3} \cdot x^{2} = x^{6}$ C、 $(π - 3.14)^{0} = 1$ D、 ${(x^{3})}^{2} = x^{5}$

查看试题解析
3. 下列运算正确的是（）

A、 $3 x^{2} + 4 x^{3} = 7 x^{5}$ B、 ${(x + y)}^{2} = x^{2} + y^{2}$ C、 $(2 + 3 x) (2 - 3 x) = 9 x^{2} - 4$ D、 $2 x y + 4 x y^{2} = 2 x y (1 + 2 y)$

查看试题解析
4. 已知 $(x + 2) (x - 2) - 2 x = 1$ ，则 $2 x^{2} - 4 x + 3$ 的值为（）

A、13 B、8 C、－3 D、5

查看试题解析
5. 已知实数m，n满足 $m^{2} + n^{2} = 2 + m n$ ，则 ${(2 m - 3 n)}^{2} + (m + 2 n) (m - 2 n)$ 的最大值为（）

A、24 B、 $\frac{44}{3}$ C、 $\frac{16}{3}$ D、-4

查看试题解析
6. 已知 ${(x + y)}^{4} = a_{1} x^{4} + a_{2} x^{3} y + a_{3} x^{2} y^{2} + a_{4} x y^{3} + a_{5} y^{4}$ ，则 $a_{1} + a_{2} + a_{3} + a_{4} + a_{5}$ 的值是（）

A、4 B、8 C、16 D、12

查看试题解析
7. 如图，是利用割补法求图形面积的示意图，下列公式中与之相对应的是（）

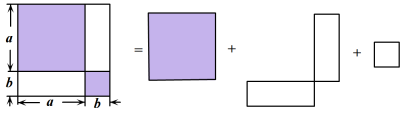A、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ B、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $(a b)^{2} = a^{2} b^{2}$

查看试题解析
8. 已知实数a，b满足 $b - a = 1$ ，则代数式 $a^{2} + 2 b - 6 a + 7$ 的最小值等于（）

A、5 B、4 C、3 D、2

查看试题解析
9. 某鞋店正举办开学特惠活动，如图为活动说明.
小彻打算在该店同时购买一双球鞋及一双皮鞋，且他有一张所有购买的商品定价皆打8折的折价券.若小彻计算后发现使用折价券与参加特惠活动两者的花费相差50元，则下列叙述何者正确？（）

A、使用折价券的花费较少，且两双鞋的定价相差100元 B、使用折价券的花费较少，且两双鞋的定价相差250元 C、参加特惠活动的花费较少，且两双鞋的定价相差100元 D、参加特惠活动的花费较少，且两双鞋的定价相差250元

查看试题解析
10. 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如：(x-y)-(z-m-n)=x-y-z+m+n，x-y-(z-m)-n = x-y-z+m-n，……，
给出下列说法：

①至少存在一种“加算操作”，使其结果与原多项式相等； ②不存在任何“加算操作”，使其结果与原多项式之和为0； ③所有的“加算操作”共有 8 种不同的结果．以上说法中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题（每题3分，共30分）

11. 单项式 $3 x y$ 的系数为．

查看试题解析
12. 计算： $m^{4} \div m^{2} =$ .

查看试题解析
13. $3 x^{2} \cdot (- 2 x y^{3})$ =

查看试题解析
14. 已知a+b=1，则代数式a²﹣b² +2b+9的值为.

查看试题解析
15. 已知 $a + b = 4$ ， $a - b = 2$ ，则 $a^{2} - b^{2}$ 的值为.

查看试题解析
16. 若一个多项式加上 $3 x y + 2 y^{2} - 8$ ，结果得 $2 x y + 3 y^{2} - 5$ ，则这个多项式为．

查看试题解析
17. 若单项式 $3 x^{m} y$ 的与 $- 2 x^{6} y$ 是同类项，则m=.

查看试题解析
18. 已知 $x + y = 4$ ， $x - y = 6$ ，则 $x^{2} - y^{2} =$ .

查看试题解析
19. 掌握地震知识，提升防震意识.根据里氏震级的定义，地震所释放出的能量 $E$ 与震级 $n$ 的关系为 $E = k \times 1 0^{1.5 n}$ （其中 $k$ 为大于0的常数），那么震级为8级的地震所释放的能量是震级为6级的地震所释放能量的倍.

查看试题解析
20. 若m+n=10，mn=5，则 $m^{2} + n^{2}$ 的值为．

查看试题解析

三、解答题（共6题，共60分）

21.

(1)、计算： $\sqrt{9} - 5 + (- 3) \times {(- 2)}^{2}$

(2)、化简： $3 a + 2 (a^{2} - a) - 2 a \cdot 3 a$ .

查看试题解析
22. 先化简，再求值：（1+x）（1﹣x）+x（x+2），其中x = $\frac{1}{2}$ ．

查看试题解析
23. 先化简，再求值：（a+2b）²+（a+2b）（a-2b）+2a（b-a），其中a＝ $\sqrt{3}$ - $\sqrt{2}$ ， b＝ $\sqrt{3}$ + $\sqrt{2}$ ．

查看试题解析
24. 已知 $a^{2} - 2 a + 1 = 0$ ，求代数式 $a (a - 4) + (a + 1) (a - 1) + 1$ 的值.

查看试题解析
25. 下面是一道例题及其解答过程的一部分，其中 $A$ 是关于 $m$ 的多项式．请写出多项式 $A$ ，并将该例题的解答过程补充完整．
例先去括号，再合并同类项： $m$ （ $A$ ） $- 6 (m + 1)$ ．
解： $m$ （ $A$ ） $- 6 (m + 1)$
$= m^{2} + 6 m - 6 m - 6$
$=$ ．

查看试题解析
26. 《几何原本》是古希腊数学家欧几里得的一部不朽著作，是数学发展史的一个里程碑.在该书的第2幕“几何与代数”部分，记载了很多利用几何图形来论证的代数结论，利用几何给人以强烈印象将抽象的逻辑规律体现在具体的图形之中.

(1)、我们在学习许多代数公式时，可以用几何图形来推理，观察下列图形，找出可以推出的代数公式，（下面各图形均满足推导各公式的条件，只需填写对应公式的序号）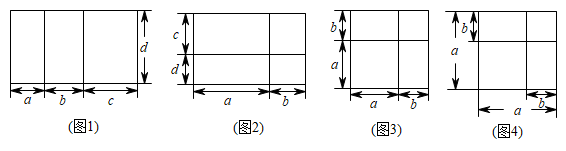

公式①： $(a + b + c) d = a d + b d + c d$

公式②： $(a + b) (c + d) = a c + a d + b c + b d$

公式③： ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

公式④： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

图1对应公式，图2对应公式，图3对应公式，图4对应公式；

(2)、《几何原本》中记载了一种利用几何图形证明平方差公式 $(a + b) (a - b) = a^{2} - b^{2}$ 的方法，如图5，请写出证明过程；（已知图中各四边形均为矩形）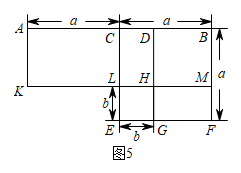

(3)、如图6，在等腰直角三角形ABC中， $∠ B A C = 90 °$ ， D为BC的中点，E为边AC上任意一点（不与端点重合），过点E作 $E G ⊥ B C$ 于点G，作 $E H ⊥ A D$ F点H过点B作BF//AC交EG的延长线于点F.记△BFG与△CEG的面积之和为 $S_{1}$ ， △ABD与△AEH的面积之和为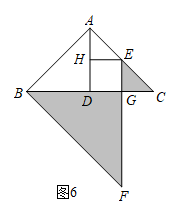 $S_{2}$ .

①若E为边AC的中点，则 $\frac{S_{1}}{S_{2}}$ 的值为 ▲ ；

②若E不为边AC的中点时，试问①中的结论是否仍成立？若成立，写出证明过程；若不成立，请说明理由.

查看试题解析