2023年中考数学复习考点一遍过——代数式

试卷更新日期：2022-12-11 类型：一轮复习

进入出卷网下载

一、填空题（每题3分，共30分）

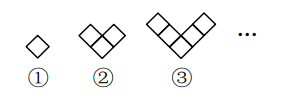
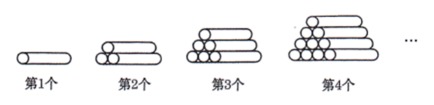
1. 已知f（x）=3x，则f（1）= ．

查看试题解析
2. 篮球队要购买10个篮球，每个篮球 $m$ 元，一共需要元．（用含 $m$ 的代数式表示）

查看试题解析
3. 按一定规律排列的数据依次为 $\frac{1}{2}$ ， $\frac{4}{5}$ ， $\frac{7}{10}$ ， $\frac{10}{17}$ ……按此规律排列，则第30个数是．

查看试题解析
4. 已知 $x^{2} - 3 x + 1 = 0$ ，则 $3 x^{2} - 9 x + 5 =$ .

查看试题解析
5. 木材加工厂将一批木料按如图所示的规律依次摆放，则第 $n$ 个图中共有木料根.

查看试题解析
6. 如图，是一个“数值转换机”的示意图．若x＝﹣5，y＝3，则输出结果为．

查看试题解析
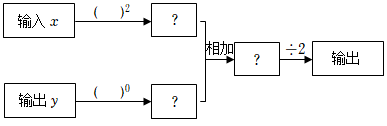7. 阅读材料：整体代值是数学中常用的方法.例如“已知 $3 a - b = 2$ ，求代数式 $6 a - 2 b - 1$ 的值.”可以这样解： $6 a - 2 b - 1 = 2 (3 a - b) - 1 = 2 \times 2 - 1 = 3$ .根据阅读材料，解决问题：若 $x = 2$ 是关于x的一元一次方程 $a x + b = 3$ 的解，则代数式 $4 a^{2} + 4 a b + b^{2} + 4 a + 2 b - 1$ 的值是.

查看试题解析
8. 如图，某链条每节长为 $2.8 cm$ ，每两节链条相连接部分重叠的圆的直径为 $1 cm$ ，按这种连接方式，50节链条总长度为 $cm$ .

查看试题解析
9. 将一组数 $\sqrt{2}$ ， 2， $\sqrt{6}$ ， $2 \sqrt{2}$ ， …， $4 \sqrt{2}$ ，按下列方式进行排列：
$\sqrt{2}$ ， 2， $\sqrt{6}$ ， $2 \sqrt{2}$ ；
$\sqrt{10}$ ， $2 \sqrt{3}$ ， $\sqrt{14}$ ， 4；
…
若2的位置记为 $(1 ， 2)$ ， $\sqrt{14}$ 的位置记为 $(2 ， 3)$ ，则 $2 \sqrt{7}$ 的位置记为.

查看试题解析
10. 观察下列图形规律，当图形中的“○”的个数和“．”个数差为2022时，n的值为．

查看试题解析

二、综合题（共4题，共60分）

11. 计算：

(1)、 $3^{2} + {(\frac{1}{3})}^{0} + {(\frac{1}{3})}^{- 1}$ ；

(2)、若 ${(a + 1)}^{2} + | b - 2 | + \sqrt{c + 3} = 0$ ，求 $a (b + c)$ 的值．

查看试题解析
12. 整式 $3 (\frac{1}{3} - m)$ 的值为P ．

(1)、当m＝2时，求P的值；

(2)、若P的取值范围如图所示，求m的负整数值．

查看试题解析
13. 观察以下等式：
第1个等式： ${(2 \times 1 + 1)}^{2} = {(2 \times 2 + 1)}^{2} - {(2 \times 2)}^{2}$ ，
第2个等式： ${(2 \times 2 + 1)}^{2} = {(3 \times 4 + 1)}^{2} - {(3 \times 4)}^{2}$ ，
第3个等式： ${(2 \times 3 + 1)}^{2} = {(4 \times 6 + 1)}^{2} - {(4 \times 6)}^{2}$ ，
第4个等式： ${(2 \times 4 + 1)}^{2} = {(5 \times 8 + 1)}^{2} - {(5 \times 8)}^{2}$ ，
……
按照以上规律．解决下列问题：

(1)、写出第5个等式：；

(2)、写出你猜想的第n个等式（用含n的式子表示），并证明．

查看试题解析
14. 设 $\bar{a 5}$ 是一个两位数，其中a是十位上的数字（1≤a≤9）．例如，当a＝4时， $\bar{a 5}$ 表示的两位数是45．

(1)、尝试：
①当a＝1时，15²＝225＝1×2×100＋25；

②当a＝2时，25²＝625＝2×3×100＋25；

③当a＝3时，35²＝1225＝；

……

(2)、归纳： ${\bar{a 5}}^{2}$ 与100a(a＋1)＋25有怎样的大小关系？试说明理由．

(3)、运用：若 ${\bar{a 5}}^{2}$ 与100a的差为2525，求a的值．

查看试题解析

三、单选题（每题3分，共30分）

15. 按一定规律排列的一组数据： $\frac{1}{2}$ ， $- \frac{3}{5}$ ， $\frac{1}{2}$ ， $- \frac{7}{17}$ ， $\frac{9}{26}$ ， $- \frac{11}{37}$ ， …．则按此规律排列的第10个数是（）

A、 $- \frac{19}{101}$ B、 $\frac{21}{101}$ C、 $- \frac{19}{82}$ D、 $\frac{21}{82}$

查看试题解析
16. 按一定规律排列的单项式：x，3x²，5x³，7x⁴ ， 9x⁵ ， ……，第n个单项式是（）

A、(2n-1) xⁿ B、(2n+1)xⁿ C、(n-1)xⁿ D、(n+1)xⁿ

查看试题解析
17. 若a，b互为相反数，c的倒数是4，则 $3 a + 3 b - 4 c$ 的值为（）

A、-8 B、-5 C、-1 D、16

查看试题解析
18. 为落实“双减”政策，某校利用课后服务开展了主题为“书香满校园”的读书活动.现需购买甲，乙两种读本共100本供学生阅读，其中甲种读本的单价为10元/本，乙种读本的单价为8元/本，设购买甲种读本x本，则购买乙种读本的费用为（）

A、 $8 x$ 元 B、 $10 (100 - x)$ 元 C、 $8 (100 - x)$ 元 D、 $(100 - 8 x)$ 元

查看试题解析
19. 周末，父子二人在一段笔直的跑道上练习竞走，两人分别从跑道两端开始往返练习．在同一直角坐标系中，父子二人离同一端的距离s（米）与时间t（秒）的关系图像如图所示．若不计转向时间，按照这一速度练习20分钟，迎面相遇的次数为（）

A、12 B、16 C、20 D、24

查看试题解析
20. 生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型.在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2ⁿ来表示.即：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，……，请你推算2²⁰²²的个位数字是（）

A、8 B、6 C、4 D、2

查看试题解析
21. 将全体正偶数排成一个三角形数阵：
按照以上排列的规律，第10行第5个数是（）

A、98 B、100 C、102 D、104

查看试题解析
22. 将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（）

A、9 B、10 C、11 D、12

查看试题解析
23. 把菱形按照如图所示的规律拼图案，其中第①个图案中有 1个菱形，第②个图案中有 3个菱形，第③个图案中有5个菱形，…，按此规律排列下去，则第⑥个图案中菱形的个数为（）

A、15 B、13 C、11 D、9

查看试题解析
24. 若 $1 0^{x} = N$ ，则称 $x$ 是以10为底 $N$ 的对数.记作： $x = l g N$ .例如： $1 0^{2} = 100$ ，则 $2 = l g 100$ ； $1 0^{0} = 1$ ，则 $0 = l g 1$ .对数运算满足：当 $M > 0$ ， $N > 0$ 时， $l g M + l g N = l g (M N)$ ，例如： $l g 3 + l g 5 = l g 15$ ，则 ${(l g 5)}^{2} + l g 5 \times l g 2 + l g 2$ 的值为（）

A、5 B、2 C、1 D、0

查看试题解析