2023年中考数学复习考点一遍过——有理数
试卷更新日期:2022-12-11 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 计算结果等于2的是( )A、 B、 C、 D、2. 下列各数是负数的是( )A、 B、 C、 D、3. 据央视6月初报道,电信5G技术赋能千行百业,打造数字经济底座.5G牌照发放三年来,三大电信运营商共投资4772亿元.把数字4772亿用科学记数法表示为( )A、 B、 C、 D、4. 用四舍五入法取近似值,将数0.0158精确到0.001的结果是( )A、0.015 B、0.016 C、0.01 D、0.025. 计算正确的是( )A、2 B、-2 C、8 D、-86. -7的绝对值是( )A、7 B、-7 C、 D、7. 下列互为倒数的是( )A、和 B、和 C、和 D、和8. 已知实数 , 在数轴上的位置如图所示,则的值是( )
 A、-2 B、-1 C、0 D、29. 如图,数轴上点A表示的数的相反数是( )
A、-2 B、-1 C、0 D、29. 如图,数轴上点A表示的数的相反数是( )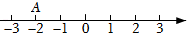 A、﹣2 B、﹣ C、2 D、310. 有理数-2, ,0, 中,绝对值最大的数是( )A、-2 B、 C、0 D、
A、﹣2 B、﹣ C、2 D、310. 有理数-2, ,0, 中,绝对值最大的数是( )A、-2 B、 C、0 D、二、填空题(每题3分,共30分)
-
11. 计算:.12. 若 , 则的值为.13. 已知 , 都是实数,若 , 则 .14. “五月天山雪,无花只有寒”,反映出地形对气温的影响.大致海拔每升高100米,气温约下降 . 有一座海拔为2350米的山,在这座山上海拔为350米的地方测得气温是 , 则此时山顶的气温约为 .15. 截止2022年1月中国向120多个国家和国际组织提供超20亿剂新冠疫苗,是对外提供此疫苗最多的国家.20亿用科学记数法表示为 .16. 小明和同学们玩扑克牌游戏.游戏规则是:从一副扑克牌(去掉“大王”“小王”)中任意抽取四张,根据牌面上的数字进行混合运算(每张牌上的数字只能用一次),使得运算结果等于24.小明抽到的牌如图所示,请帮小明列出一个结果等于24的算式 .
 17. 中国是世界上首先使用负数的国家.两千多年前战国时期李悝所著的《法经》中已出现使用负数的实例.《九章算术》的“方程”一章,在世界数学史上首次正式引入负数及其加减法运算法则,并给出名为“正负术”的算法.请计算以下涉及“负数”的式子的值: .18. 计算:-12+|-2023|= .19. 袁隆平院士被誉为“杂交水稻之父”,经过他带领的团队多年努力,目前我国杂交水稻种植面积约为2.5亿亩.将250000000用科学记数法表示为 ,则 .20. 当今大数据时代,“二维码”具有存储量大.保密性强、追踪性高等特点,它己被广泛应用于我们的日常生活中,尤其在全球“新冠”疫情防控期间,区区“二维码”已经展现出无穷威力.看似“码码相同”,实则“码码不同”.通常,一个“二维码”由1000个大大小小的黑白小方格组成,其中小方格专门用做纠错码和其他用途的编码,这相当于1000个方格只有200个方格作为数据码.根据相关数学知识,这200个方格可以生成个不同的数据二维码,现有四名网友对的理解如下:
17. 中国是世界上首先使用负数的国家.两千多年前战国时期李悝所著的《法经》中已出现使用负数的实例.《九章算术》的“方程”一章,在世界数学史上首次正式引入负数及其加减法运算法则,并给出名为“正负术”的算法.请计算以下涉及“负数”的式子的值: .18. 计算:-12+|-2023|= .19. 袁隆平院士被誉为“杂交水稻之父”,经过他带领的团队多年努力,目前我国杂交水稻种植面积约为2.5亿亩.将250000000用科学记数法表示为 ,则 .20. 当今大数据时代,“二维码”具有存储量大.保密性强、追踪性高等特点,它己被广泛应用于我们的日常生活中,尤其在全球“新冠”疫情防控期间,区区“二维码”已经展现出无穷威力.看似“码码相同”,实则“码码不同”.通常,一个“二维码”由1000个大大小小的黑白小方格组成,其中小方格专门用做纠错码和其他用途的编码,这相当于1000个方格只有200个方格作为数据码.根据相关数学知识,这200个方格可以生成个不同的数据二维码,现有四名网友对的理解如下:YYDS(永远的神):就是200个2相乘,它是一个非常非常大的数;
DDDD(懂的都懂):等于;
JXND(觉醒年代):的个位数字是6;
QGYW(强国有我):我知道 , 所以我估计比大.
其中对的理解错误的网友是(填写网名字母代号).
三、综合题(共7题,共60分)
-
21. 计算: .22. “绿水青山就是金山银山”.科学研究表明:树叶在光合作用后产生的分泌物能够吸附空气中的悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少 , 若一片国槐树叶与一片银杏树叶一年的平均滞尘总量为.(1)、请分别求出一片国槐树叶和一片银杏树叶一年的平均滞尘量;(2)、娄底市双峰县九峰山森林公园某处有始于唐代的三棵银杏树,据估计三棵银杏树共有约50000片树叶.问这三棵银杏树一年的平均滞尘总量约多少千克?23. 计算:(-6) ×( -■)-23 .
圆圆在做作业时,发现题中有一个数字被墨水污染了。
(1)、如果被污染的数字是 .请计算(-6)×( - )-23 .(2)、如果计算结果等于6,求被污染的数字.24. 今年,某市举办了一届主题为“强国复兴有我”的中小学课本剧比赛.某队伍为参赛需租用一批服装,经了解,在甲商店租用服装比在乙商店租用服装每套多10元,用500元在甲商店租用服装的数量与用400元在乙商店租用服装的数量相等.(1)、求在甲,乙两个商店租用的服装每套各多少元?(2)、若租用10套以上服装,甲商店给以每套九折优惠.该参赛队伍准备租用20套服装,请问在哪家商店租用服装的费用较少,并说明理由.25. 某单位准备购买文化用品,现有甲、乙两家超市进行促销活动,该文化用品两家超市的标价均为10元/件,甲超市一次性购买金额不超过400元的不优惠,超过400元的部分按标价的6折售卖;乙超市全部按标价的8折售卖.(1)、若该单位需要购买30件这种文化用品,则在甲超市的购物金额为元;乙超市的购物金额为元;(2)、假如你是该单位的采购员,你认为选择哪家超市支付的费用较少?26. 第十四届国际数学教育大会(ICME-14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745.八进制是以8作为进位基数的数字系统,有0~7共8个基本数字.八进制数3745换算成十进制数是 , 表示ICME-14的举办年份. (1)、八进制数3746换算成十进制数是;(2)、小华设计了一个进制数143,换算成十进制数是120,求的值.27. 健康生技公司培养绿藻以制作「绿藻粉」,再经过后续的加工步骤,制成绿藻相关的保健食品.已知该公司制作每1公克的「绿藻粉」需要60亿个绿藻细胞.
(1)、八进制数3746换算成十进制数是;(2)、小华设计了一个进制数143,换算成十进制数是120,求的值.27. 健康生技公司培养绿藻以制作「绿藻粉」,再经过后续的加工步骤,制成绿藻相关的保健食品.已知该公司制作每1公克的「绿藻粉」需要60亿个绿藻细胞.请根据上述信息回答下列问题,完整写出你的解题过程并详细解释:
(1)、假设在光照充沛的环境下,1个绿藻细胞每20小时可分裂成4个绿藻细胞,且分裂后的细胞亦可继续分裂.今从1个绿藻细胞开始培养,若培养期间绿藻细胞皆未死亡且培养环境的光照充沛,经过15天后,共分裂成4k个绿藻细胞,则k之值为何?(2)、承(1),已知60亿介于与之间,请判断4k个绿藻细胞是否足够制作8公克的「绿藻粉」?