初中数学浙教版2022-2023学年九年级下册3.4 简单几何体的表面展开图 同步练习
试卷更新日期:2022-12-10 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图所示,是一个正方体纸盒的展开图,若在其中的三个正方形 , , 分别填入适当的数,使得它们折成正方体后相对面上的两个数互为相反数,则填入正方形 , , 的三个数依次为( )
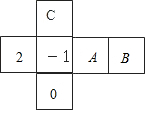 A、1,-2,0 B、-2,1,0 C、-2,0,1 D、0,-2,12. 下列哪个图形不可能是正方体的表面展开图( )A、
A、1,-2,0 B、-2,1,0 C、-2,0,1 D、0,-2,12. 下列哪个图形不可能是正方体的表面展开图( )A、 B、
B、 C、
C、 D、
D、 3. 若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和相等,则的值为( )
3. 若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和相等,则的值为( )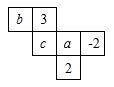 A、12 B、7 C、5 D、-54. 现有①②③④四种型号的铁皮,铁皮的形状与相关尺寸如图所示(单位:dm).从中选两种,正好可以制成一个无盖圆柱形水桶(不计接头),则所选的这两种铁皮的型号是( )
A、12 B、7 C、5 D、-54. 现有①②③④四种型号的铁皮,铁皮的形状与相关尺寸如图所示(单位:dm).从中选两种,正好可以制成一个无盖圆柱形水桶(不计接头),则所选的这两种铁皮的型号是( ) A、①③ B、①④ C、②④ D、②③5. 下图所示的长方形(长为14,宽为8)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( )
A、①③ B、①④ C、②④ D、②③5. 下图所示的长方形(长为14,宽为8)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( ) A、56 B、40 C、28 D、206. 如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y的值是( )
A、56 B、40 C、28 D、206. 如图,该平面展开图按虚线折叠成正方体后,相对面上两个数之和为8,则x+y的值是( ) A、7 B、8 C、9 D、107. 如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )
A、7 B、8 C、9 D、107. 如图1所示,将长为6的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等,若要将其围成如图2所示的三棱柱形物体,则图中a的值可以是( )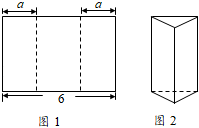 A、1 B、2 C、3 D、48. 如图,一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是圆,关于这个几何体的说法错误的是( )
A、1 B、2 C、3 D、48. 如图,一个空间几何体的主视图和左视图都是边长为2的正方形,俯视图是圆,关于这个几何体的说法错误的是( ) A、该几何体是圆柱 B、几何体底面积是 C、主视图面积是4 D、几何体侧面积是9. 如图是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
A、该几何体是圆柱 B、几何体底面积是 C、主视图面积是4 D、几何体侧面积是9. 如图是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )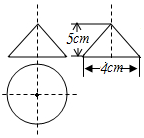 A、 B、 C、 D、10. 如图是一个不完整的正方体平面展开图,需再添上一个面,折叠后才能围成一个正方体.下面是四位同学补画的情况(图中阴影部分),其中正确的是( )
A、 B、 C、 D、10. 如图是一个不完整的正方体平面展开图,需再添上一个面,折叠后才能围成一个正方体.下面是四位同学补画的情况(图中阴影部分),其中正确的是( )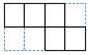 A、
A、 B、
B、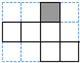 C、
C、 D、
D、
二、填空题(每题3分,共15分)
-
11. 如图.长方体的底面是边长2cm的正方形,高为6cm.如果从点A开始经过4个侧面缠绕2圈到达B,那么所用细线最短需要cm.
 12. 把一个正方体纸盒展成一个平面图形,至少需要剪开条棱.13. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
12. 把一个正方体纸盒展成一个平面图形,至少需要剪开条棱.13. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).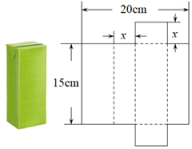 14. 如图,圆锥的母线长 , 底面圆的周长是 , 则圆锥的侧面积是 .
14. 如图,圆锥的母线长 , 底面圆的周长是 , 则圆锥的侧面积是 . 15. 如图1是三个直立于水面上的形状完全相同的几何体(下底面为圆面,单位:厘米),将它们拼成如图2的新几何体,求该新几何体的体积(结果保留);
15. 如图1是三个直立于水面上的形状完全相同的几何体(下底面为圆面,单位:厘米),将它们拼成如图2的新几何体,求该新几何体的体积(结果保留);
三、解答题(共8题,共55分)
-
16. 如图(1)是边长为60cm的正方形纸板,裁掉阴影部分后将其折叠成如图(2)所示的长方体盒子,已知该长方体的宽是高的2倍,求长方体盒子的体积.
 17. 如图是一个立体图形在三个方向上的形状图,请根据在三个方向的形状图写出该立体图形的名称,并计算该立体图形的体积.(结果保留π)
17. 如图是一个立体图形在三个方向上的形状图,请根据在三个方向的形状图写出该立体图形的名称,并计算该立体图形的体积.(结果保留π) 18. 如图,在四边形ABCD中,AD∥BC,AD=2,AB=2 , 以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.若扇形AFD是一个圆锥的侧面,求这个圆锥的底面圆的半径.
18. 如图,在四边形ABCD中,AD∥BC,AD=2,AB=2 , 以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.若扇形AFD是一个圆锥的侧面,求这个圆锥的底面圆的半径. 19. 每个正方体相对两个面上写的数之和等于2.
19. 每个正方体相对两个面上写的数之和等于2.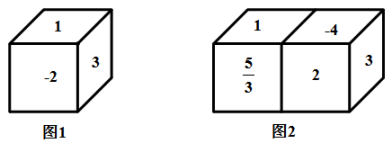 (1)、求图1的正方体看不见的三个面上的数字的积.(2)、现将两个这样的正方体黏合放置(如图2),求所有看不见的七个面上所写的数字的和.20. 如图,是一个几何体的表面展开图.
(1)、求图1的正方体看不见的三个面上的数字的积.(2)、现将两个这样的正方体黏合放置(如图2),求所有看不见的七个面上所写的数字的和.20. 如图,是一个几何体的表面展开图. (1)、该几何体是 .(2)、依据图中数据求该几何体的表面积和体积.21. 如图,在单位长度为1的正方形网格中建立直角坐标系,一条圆弧恰好经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
(1)、该几何体是 .(2)、依据图中数据求该几何体的表面积和体积.21. 如图,在单位长度为1的正方形网格中建立直角坐标系,一条圆弧恰好经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号): (1)、利用网格找出该圆弧所在圆的圆心D点的位置,则D点的坐标为;(2)、连接AD、CD,若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为;(3)、连接AB,将线段AB绕点D旋转一周,求线段AB扫过的面积.22. 妈妈给圆柱形的玻璃杯(底面直径16cm,高20cm)做了一个布套(包住侧面)
(1)、利用网格找出该圆弧所在圆的圆心D点的位置,则D点的坐标为;(2)、连接AD、CD,若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为;(3)、连接AB,将线段AB绕点D旋转一周,求线段AB扫过的面积.22. 妈妈给圆柱形的玻璃杯(底面直径16cm,高20cm)做了一个布套(包住侧面) (1)、求出至少用布料多少平方厘米?(2)、求这个杯子最多可以盛水多少立方厘米?23. 【问题情境】
(1)、求出至少用布料多少平方厘米?(2)、求这个杯子最多可以盛水多少立方厘米?23. 【问题情境】小圣所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔.

【操作探究】
(1)、图1中的哪些图形经过折叠能围成无盖正方体纸盒?(填序号).(2)、小圣所在的综合实践小组把折叠成6个棱长都为的无盖正方体纸盒摆成如图2所示的几何体.①请计算出这个几何体的体积;
②如果在这个几何体上再添加一些相同的正方体纸盒,并保持从上面看到的形状和从左面看到的形状不变,最多可以再添加 个正方体纸盒.