山东省泰安市2022-2023学年高三上学期数学期中考试试卷

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x = 3 n + 2 ， n \in N} ， B = {2 ， 4 ， 6 ， 8 ， 10 ， 12 ， 14}$ ，则集合 $A \cap B$ 中元素的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 已知命题 $p ： \forall a \in (0 ， + \infty)$ ， $a + \frac{1}{a} > 2$ 则 $\neg p$ 是（）

A、 $\exists a \in (0 ， + \infty)$ ， $a + \frac{1}{a} > 2$ B、 $\exists a \notin (0 ， + \infty)$ ， $a + \frac{1}{a} > 2$ C、 $\exists a \in (0 ， + \infty)$ ， $a + \frac{1}{a} \leq 2$ D、 $\exists a \notin (0 ， + \infty)$ ， $a + \frac{1}{a} \leq 2$

查看试题解析
3. “ $a > b > c$ ”是“ $a b > a c$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 下列函数中，是奇函数且在其定义域上为增函数的是（）

A、 $y = \sin x$ B、 $y = x | x |$ C、 $y = \tan x$ D、 $y = x - \frac{1}{x}$

查看试题解析
5. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n} (n \in N^{*})$ ，若 $a_{1} = 2 ， S_{15} = - 30$ ，则满足 $a_{n} \cdot a_{n + 1} < 0$ 的 $n$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
6. 函数 $f (x) = \frac{2 x^{2}}{e^{x} + e^{- x}}$ 的部分图象大致为（）

A、 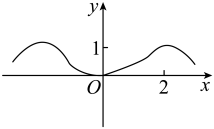B、 C、 D、

查看试题解析
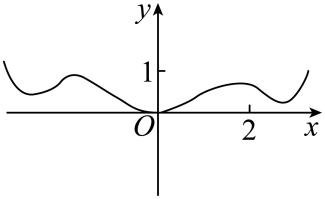7. 根据《民用建筑工程室内环境污染控制标准》，文化娱乐场所室内甲醛浓度 $\leq 0.1 mg / m^{3}$ 为安全范围.已知某新建文化娱乐场所施工中使用了甲醛喷剂，处于良好的通风环境下时，竣工1周后室内甲醛浓度为 $6.25 mg / m^{3}$ ，3周后室内甲醛浓度为 $1 mg / m^{3}$ ，且室内甲醛浓度 $ρ (t)$ （单位： $mg / m^{3}$ ）与竣工后保持良好通风的时间 $t (t \in N^{*})$ （单位：周）近似满足函数关系式 $ρ (t) = e^{a t + b}$ ，则该文化娱乐场所竣工后的甲醛浓度若要达到安全开放标准，至少需要放置的时间为（）

A、5周 B、6周 C、7周 D、8周

查看试题解析
8. 已知 $e^{a} = 1.02 ， b = \sqrt{1.04} - 1 ， (\sqrt{e})^{c} = 1.01$ ，则（）

A、 $a < b < c$ B、 $b < a < c$ C、 $b < c < a$ D、 $c < a < b$

查看试题解析

二、多选题

9. 在公比为 $q$ 等比数列 ${a_{n}}$ 中， $S_{n}$ 是数列 ${a_{n}}$ 的前n项和，若 $a_{1} = 1 ， a_{5} = 27 a_{2}$ ，则下列说法正确的是（）

A、 $q = 3$ B、数列 ${S_{n} + 2}$ 是等比数列 C、 $S_{5} = 121$ D、 $2 \lg a_{n} = \lg a_{n - 2} + \lg a_{n + 2} (n \geq 3)$

查看试题解析
10. 已知函数 $f (x) = s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的图象如图所示，则（）

A、点 $(\frac{7 π}{6} ， 0)$ 为函数 $f (x)$ 图象的一个对称中心 B、函数 $f (x)$ 在 $(\frac{π}{2} ， π)$ 上单调递减 C、函数 $f (x)$ 的图象与 $y$ 轴的交点为 $(0 ， - \frac{\sqrt{3}}{2})$ D、若函数 $f (x + θ)$ 为偶函数，则 $θ = k π + \frac{5 π}{12} ， k \in Z$

查看试题解析
11. 下列说法正确的是（）

A、若 $a > b > 0 ， c < d < 0$ ，则一定有 $\frac{b}{c} > \frac{a}{d}$ B、若关于 $x$ 的不等式 $a x^{2} - x - b < 0$ 的解集为 ${x | 2 < x < 3}$ ，则 $a + b = 1$ C、若 $x > 0 ， y > 0 ， x y + x + y = 8$ ，则 $x + y$ 的最小值为4 D、若 $a > 0 ， b \geq 0$ ，且 $a + b = 1$ ，则 $\frac{b (3 - b)}{a}$ 的最小值为0

查看试题解析
12. 已知 $f (x) = x - \frac{x^{2}}{π} - \sin x$ .（）

A、 $f (x)$ 的零点个数为4 B、 $f (x)$ 的极值点个数为3 C、x轴为曲线 $y = f (x)$ 的切线 D、若 $f (x_{1}) = f (x_{2})$ ，则 $x_{1} + x_{2} = π$

查看试题解析

三、填空题

13. 已知角 $α$ 的终边过点 $(3 ， 1)$ ，则 $\frac{s i n 2 α + 1}{c o s 2 α} =$ .

查看试题解析
14. “中国剩余定理”又称“孙子定理”.“中国剩余定理”讲的是一个关于整除的问题.现有这样一个整除问题：将1到100这100个数中，能被2除余1且被3除余1的数按从小到大的顺序排成一列，构成数列 ${a_{n}}$ ，则数列 ${a_{n}}$ 各项的和为.

查看试题解析
15. 已知函数 $f (x)$ 是定义在R上的偶函数，且对任意实数 $x$ 都有 $f (x) + f (2 - x) = 0$ ，当 $x \in [- 1 ， 0]$ 时， $f (x) = 2^{x} - \frac{1}{2}$ ，则 $f (l o g_{2} 63) =$ .

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} l o g_{2} (x + 1) ， x > 3 \\ \frac{1}{3} | x + 3 | ， - 9 \leq x \leq 3 \end{array}$ ，若 $x_{1} < x_{2} ， x_{1} < x_{3}$ 且 $f (x_{1}) = f (x_{2}) ， f (x_{1}) + f (x_{3}) = 4$ ，则 $\frac{x_{3}}{x_{1} + x_{2}}$ 的取值范围是.

查看试题解析

四、解答题

17. 已知集合 $A = {x | x > 0} ， B = {x | x^{2} - a x + 2 a > 0 ， a \in R}$ .

(1)、若 $B = R$ ，求 $a$ 的取值范围；

(2)、若 $a \geq 9$ ，求 $A \cap B$ .

查看试题解析
18. 在△ $A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，且满足 $\sqrt{3} c o s A (c c o s B + b c o s C) = a s i n A$ .

(1)、求 $A$ ；

(2)、已知 $D$ 为 $B C$ 边上一点， $A D$ 平分 $∠ A$ ， △ $A B D$ 的面积是△ $A D C$ 的面积的2倍，若 $B D = 2$ ，求 $A D$ .

查看试题解析
19. 已知函数 $f (x) = (2 s i n^{2} x - a) c o s (2 x + θ) (θ \in [0 ， π])$ 为奇函数，且 $f (\frac{π}{3}) = - \frac{\sqrt{3}}{4}$ .

(1)、若： $f (\frac{α}{4}) = \frac{2}{5} ， α \in (\frac{π}{2} ， π)$ ，求 $s i n (α + \frac{π}{3})$ ；

(2)、将函数 $y = f (x)$ 的图使上各点的横坐标变为原来为2倍（纵坐标不变），再将得到的函数图象向左平移 $\frac{π}{6}$ 个单位长度，得到函数 $y = g (x)$ 的图象，求函数 $g (x)$ 在 $[0 ， \frac{π}{6}]$ 上的值域.

查看试题解析
20. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n} ， a_{1} = 1 ， a_{2} = 2 ， 2 S_{n} = a_{n + 2} + a_{n + 1} - 3$ .

(1)、求 $S_{n}$ ；

(2)、设 $b_{n} = \frac{1}{S_{2 n}} ， {b_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，求证： $T_{n} < \frac{1}{2}$

查看试题解析
21. 某群体的人均通勤时间，是指单日内该群体成员从居住地到工作地的平均用时.某地上班族 $S$ 中的成员仅以自驾或公交方式通勤，分析显示：当 $S$ 中 $x % (0 < x < 100)$ 的成员自驾时，自驾群体的人均通勤时间为 $f (x) = {\begin{array}{l} 20 + \frac{x}{5} ， 0 < x ⩽ 30 \\ 2 x + \frac{k}{x} - 94 ， 30 < x < 100 \end{array}$ （单位：分钟）；公交群体的人均通勤时间为 $g (x) = 36 - \frac{x}{10}$ （单位：分钟）.已知当 $x = 40$ 时，公交群体的人均通勤时间比自驾群体的人均通勤时间长1分钟.

(1)、求 $k$ 的值；

(2)、求该地上班族 $S$ 的最短人均通勤时间.

查看试题解析
22. 已知函数 $f (x) = e^{x} - a x - 1 ， a \in R$ .

(1)、求函数 $f (x)$ 的极值；

(2)、若1是关于 $x$ 的方程 $f (x) = b x^{2} (b \in R)$ 的根，且方程 $f (x) = b x^{2}$ 在 $(0 ， 1)$ 上有实根，求 $b$ 的取值范围.

查看试题解析