河北省冀东名校2022-2023学年高三上学期数学期中调研考试试卷

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 设集合 $A = {x ∣ x^{2} - 7 x + 12 = 0}$ ， $B = {1 ， 3 ， 5}$ ， $C = {0 ， 2 ， 4}$ ，则 $(A \cap B) \cup C =$ （）

A、 ${0 ， 2}$ B、 ${3 ， 4 ， 5}$ C、 ${3 ， 4}$ D、 ${0 ， 2 ， 3 ， 4}$

查看试题解析
2. 已知 $z = (3 - i) (1 + 2 i)$ ，则z的虚部为（）

A、5 B、 $5 i$ C、 $- 1$ D、 $- i$

查看试题解析
3. 某工厂利用随机数表对生产的50个零件进行抽样测试，先将50个零件进行编号，编号分别为01，02，…，50，从中抽取5个样本，下面提供随机数表的第1行到第2行：
$\begin{array}{l} 66 & 67 & 40 & 37 & 14 & 64 & 05 & 71 & 11 & 05 & 65 & 09 & 95 & 86 & 68 & 76 & 83 & 20 & 37 & 90 \\ 57 & 16 & 03 & 11 & 63 & 14 & 90 & 84 & 45 & 21 & 75 & 73 & 88 & 05 & 90 & 52 & 23 & 59 & 43 & 10 \end{array}$
若从表中第1行第9列开始向右依次读取数据，则得到的第4个样本编号是（）

A、10 B、09 C、71 D、20

查看试题解析
4. 若函数 $f (x) = \frac{a x - 2}{x - 1}$ 的图像关于点 $(1 ， 3)$ 对称，则实数 $a =$ （）

A、5 B、3 C、6 D、2

查看试题解析
5. 已知直线 $a x + 2 b y - 1 = 0$ 和 $x^{2} + y^{2} = 1$ 相切，则 $a b$ 的最大值是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看试题解析
6. 在梯形ABCD中， $A B / / C D$ ， $∠ A = 9 0^{°}$ ， $A B = 2 C D = 3$ ， $A D = 2$ ，若EF在线段AB上运动，且 $E F = 1$ ，则 $\vec{C E} \cdot \vec{C F}$ 的最小值为（）

A、5 B、 $\sqrt{3}$ C、4 D、 $\frac{15}{4}$

查看试题解析
7. 多面体欧拉定理是指对于简单多面体，其各维对象数总满足一定的数量关系，在三维空间中，多面体欧拉定理可表示为：顶点数＋表面数－棱长数＝2.在数学上，富勒烯的结构都是以正五边形和正六边形面组成的凸多面体，例如富勒烯 $C_{60}$ （结构图如图）是单纯用碳原子组成的稳定分子，具有60个顶点和32个面，其中12个为正五边形，20个为正六边形.除 $C_{60}$ 外具有封闭笼状结构的富勒烯还可能有 $C_{28}$ ， $C_{32}$ ， $C_{50}$ ， $C_{70}$ ， $C_{84}$ ， $C_{240}$ ， $C_{540}$ ，等，则 $C_{84}$ 结构含有正六边形的个数为（）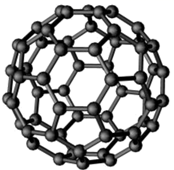

A、12 B、24 C、30 D、32

查看试题解析
8. 函数 $f (x) = c o s x + x s i n x - \frac{1}{4} x^{2} - 1$ 零点的个数为（）

A、0 B、1 C、2 D、3

查看试题解析

二、多选题

9. 若 ${(x^{2} + \frac{1}{a x})}^{6}$ 的展开式中 $x^{3}$ 的系数是 $- 160$ ，则（）

A、 $a = - \frac{1}{2}$ B、所有项系数之和为1 C、二项式系数之和为 $64$ D、常数项为 $- 320$

查看试题解析
10. 在数列 ${a_{n}}$ 中，若 $a_{n} + a_{n + 1} = 3^{n}$ ，则称 ${a_{n}}$ 为“和等比数列”．设 $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和，且 $a_{1} = 1$ ，则下列对“和等比数列”的判断中正确的有（）

A、 $a_{2020} = \frac{3^{2020} - 1}{4}$ B、 $a_{2020} = \frac{3^{2021} - 1}{4}$ C、 $S_{2021} = \frac{3^{2022} - 1}{8}$ D、 $S_{2021} = \frac{3^{2023} - 1}{8}$

查看试题解析
11. 如图， $P$ 为椭圆 $C_{1}$ ： $\frac{x^{2}}{8} + \frac{y^{2}}{6} = 1$ 上的动点，过 $P$ 作椭圆 $C_{1}$ 的切线交圆 $C_{2}$ ： $x^{2} + y^{2} = 24$ 于 $M$ ， $N$ ，过 $M$ ， $N$ 作 $C_{2}$ 切线交于 $Q$ ，则（）

A、 $S_{△ O P Q}$ 的最大值为 $\sqrt{3}$ B、 $S_{△ O P Q}$ 的最大值为 $\frac{2 \sqrt{3}}{3}$ C、 $Q$ 的轨迹方程是 $\frac{x^{2}}{36} + \frac{y^{2}}{48} = 1$ D、 $Q$ 的轨迹方程是 $\frac{x^{2}}{72} + \frac{y^{2}}{96} = 1$

查看试题解析
12. 已知C是以AB为直径的圆O上异于A，B的点，平面PAC⊥平面ABC，
$P A = P C = A C = 2$ ， $B C = 4$ ， E，F分别是PC，PB的中点，平面AEF与平面ABC的交线为直线l，点Q为直线l上动点，则直线PQ与平面AEF所成的角的取值可以为（）

A、0° B、15° C、30° D、45°

查看试题解析

三、填空题

13. 为庆祝冬奥会取得胜利，甲、乙两位同学参加知识竞赛.已知两人答题正确与否相互独立，且各一次正确的概率分别是0.4和0.3，则甲、乙两人各作答一次，至少有一人正确的概率为

查看试题解析
14. 若 $t a n (\frac{9 π}{4} - α) = - \frac{3}{5}$ ，则 $c o s 2 α =$

查看试题解析
15. 定义n个正数 $p_{1} ， p_{2} ， \dots ， p_{n}$ 的“均倒数”为 $\frac{n}{p_{1} + p_{2} + \cdot \cdot \cdot + p_{n}}$ ，若各项均为正数的数列 ${a_{n}}$ 的前n项的“均倒数”为 $\frac{1}{2 n + 1}$ ，则 $a_{2023}$ 的值为

查看试题解析
16. 《益古演段》是我国古代数学家李冶（1192～1279）的一部数学著作.内容主要是已知平面图形的信息，求圆的半径、正方形的边长和周长等等.其中有这样一个问题：如图，已知 $∠ A = 60 °$ ，点 $B$ 、 $C$ 分别在 $∠ A$ 的两个边上移动，且保持 $B$ 、 $C$ 两点间的距离为 $2 \sqrt{3}$ ，则点 $B$ 、 $C$ 在移动过程中，线段 $B C$ 的中点 $D$ 到点 $A$ 的最大距离为．

查看试题解析

四、解答题

17. 如图所示，在四边形ABCD中， $A C = A D = C D = 7$ ， $∠ A B C = 12 0^{°}$ ， $s i n ∠ B A C = \frac{5 \sqrt{3}}{14}$

(1)、求BC；

(2)、若BD为 $∠ A B C$ 的平分线，试求BD．

查看试题解析
18. 数列{an}满足： $a_{1} = 1$ ，点 $(n ， a_{n} + a_{n + 1})$ 在函数 $y = k x + 1$ 的图象上，其中k为常数，且 $k \neq 0$ .

(1)、若 $a_{1}$ ， $a_{2}$ ， $a_{4}$ 成等比数列，求k的值；

(2)、当 $k = 3$ 时，求数列 ${a_{n}}$ 的前 $2 n$ 项的和 $S_{2 n}$

查看试题解析
19. 如图①，在梯形 $A B C D$ 中， $B C / / A D$ ， $A D = 4$ ， $B C = 1$ ， $∠ A D C = 4 5^{°}$ ，梯形的高为1，M为AD的中点，以BM为折痕将△ABM折起，使点A到达点N的位置，且平面NBM⊥平面BCDM，连接NC，ND，如图②.

(1)、证明：平面NMC⊥平面NCD；

(2)、求图②中平面NBM与平面NCD夹角的余弦值.

查看试题解析
20. 为调查某社区居民进行核酸检测的地点，随机调查了该社区80人，得到下面的数据表：
单位：人
性别
核酸检测地点
合计
工作单位
社区
男
10
50
60
女
10
10
20
合计
20
60
80

(1)、根据小概率值α＝0.01的独立性检验，能否认为“居民的核酸检测地点与性别有关系”？

(2)、将此样本的频率估计为总体的概率，在该社区的所有男性中随机调查3人，设调查的3人以社区为核酸检测地点的人数为随机变量X，求X的数学期望和方差.

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{4} + y^{2} = 1$ ，点P为椭圆C上非顶点的动点，点 $A_{1}$ ， $A_{2}$ 分别为椭圆C的左、右顶点，过 $A_{1}$ ， $A_{2}$ 分别作 $l_{1} ⊥ P A_{1}$ ， $l_{2} ⊥ P A_{2}$ ，直线 $l_{1}$ ， $l_{2}$ 相交于点G，连接OG（O为坐标原点），线段OG与椭圆C交于点Q.若直线OP，OQ的斜率分别为 $k_{1}$ ， $k_{2}$ .

(1)、求 $\frac{k_{1}}{k_{2}}$ 的值；

(2)、求 $△ P O Q$ 面积的最大值.

查看试题解析
22. 已知函数 $f (x) = 2 e^{x} + a (x^{2} - l n x) + x$ .

(1)、若 $a = - 2 e - 1$ ，求 $f (x)$ 的单调区间；

(2)、记函数 $g (x) = - x^{2} - a l n (x + 1) + x + 4$ ，若 $f (x + 1) \geq g (x)$ 恒成立，试求实数 $a$ 的取值范围.

查看试题解析

性别	核酸检测地点		合计
性别	工作单位	社区	合计
男	10	50	60
女	10	10	20
合计	20	60	80