天津市武清区2022~2023学年八年级上学期期中数学试卷
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 如果一个三角形的两边长分别是 和 ,则第三边长可能是( )A、 B、 C、 D、2. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在 中, , ,则下列判断错误的是( )A、 是直角三角形 B、 是等腰三角形 C、 是锐角三角形 D、 和 互余4. 若等腰三角形的两边长为和 , 则周长为( )A、 B、 C、或 D、以上都不对5. 如图,在△ABC中,AB=AC , D为BC中点,∠BAD=35°,则∠C的度数为( )
3. 在 中, , ,则下列判断错误的是( )A、 是直角三角形 B、 是等腰三角形 C、 是锐角三角形 D、 和 互余4. 若等腰三角形的两边长为和 , 则周长为( )A、 B、 C、或 D、以上都不对5. 如图,在△ABC中,AB=AC , D为BC中点,∠BAD=35°,则∠C的度数为( ) A、35° B、45° C、55° D、60°6. 如图,已知△ABC≌△CDE,其中AB=CD,错误的是( )
A、35° B、45° C、55° D、60°6. 如图,已知△ABC≌△CDE,其中AB=CD,错误的是( ) A、AC=CE B、∠BAC=∠DCE C、∠ACB=∠ECD D、∠B=∠D7. 如图,已知AB=AD,∠BAD=∠CAE,则添加下列条件之一,仍不一定能判定△ABC≌△ADE的是( )
A、AC=CE B、∠BAC=∠DCE C、∠ACB=∠ECD D、∠B=∠D7. 如图,已知AB=AD,∠BAD=∠CAE,则添加下列条件之一,仍不一定能判定△ABC≌△ADE的是( ) A、AC=AE B、∠C=∠E C、BC=DE D、∠B=∠D8. 在等腰三角形中,有一个角是50°,它的一条腰上的高与底边的夹角是( )A、25° B、25°或40° C、30°或40° D、50°9. 下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )A、①②③ B、①②④ C、①③ D、①②③④10. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
A、AC=AE B、∠C=∠E C、BC=DE D、∠B=∠D8. 在等腰三角形中,有一个角是50°,它的一条腰上的高与底边的夹角是( )A、25° B、25°或40° C、30°或40° D、50°9. 下列三角形:①有两个角等于60°;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )A、①②③ B、①②④ C、①③ D、①②③④10. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( ) A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC11. 如图,在中, , AD,CE是的两条中线,P是AD上的一个动点,则下列线段的长等于最小值的是( )
A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC11. 如图,在中, , AD,CE是的两条中线,P是AD上的一个动点,则下列线段的长等于最小值的是( )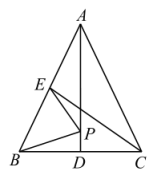 A、AC B、BC C、AD D、CE12. 如图,在中,已知 , , , 的平分线与边交于点D,于点E,则的周长为( )
A、AC B、BC C、AD D、CE12. 如图,在中,已知 , , , 的平分线与边交于点D,于点E,则的周长为( ) A、 B、2 C、 D、无法计算
A、 B、2 C、 D、无法计算二、填空题
-
13. 如图,的大小关系是(填>,=或<).
 14. 如图,已知∠C=∠D , ∠ABC=∠BAD , AC与BD相交于点E , 请你写出图中一组相等的线段 . (写出一组即可)
14. 如图,已知∠C=∠D , ∠ABC=∠BAD , AC与BD相交于点E , 请你写出图中一组相等的线段 . (写出一组即可) 15. 如果一个多边形的每个外角都等于 , 那么这个多边形是边形.16. 如图为6个边长相等的正方形的组合图形,则 .
15. 如果一个多边形的每个外角都等于 , 那么这个多边形是边形.16. 如图为6个边长相等的正方形的组合图形,则 . 17. 如图, 中, 是 的垂直平分线, , 的周长为 , 则 的周长为 .
17. 如图, 中, 是 的垂直平分线, , 的周长为 , 则 的周长为 . 18. 在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标 .
18. 在平面直角坐标系中,已知点A(1,2),B(5,5),C(5,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标 .三、解答题
-
19. 如图,三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
 (1)、画出关于y轴对称的 ,(2)、写出三个顶点坐标分别为: , , ;(3)、求的面积?20. 如图,已知 , 点D在上,与交于点P.若 , , 求的度数.
(1)、画出关于y轴对称的 ,(2)、写出三个顶点坐标分别为: , , ;(3)、求的面积?20. 如图,已知 , 点D在上,与交于点P.若 , , 求的度数. 21. 如图,已知锐角三角形的两条高相交于点O,且 . 请你判断的形状,并说明理由.
21. 如图,已知锐角三角形的两条高相交于点O,且 . 请你判断的形状,并说明理由. 22. 如图,已知是等边三角形,D是延长线上一点,平分 , 且 .
22. 如图,已知是等边三角形,D是延长线上一点,平分 , 且 .
求证:
(1)、;(2)、为等边三角形.23. 如图,一条船上午8时从海岛A出发,以15海里/时的速度向正北方向航行,上午10时到达海岛B处,分别从A,B处望灯塔C,测得∠NAC=30°,∠NBC=60°. (1)、求海岛B到灯塔C的距离;(2)、若这条船继续向正北航行,问什么时间小船与灯塔C的距离最短?
(1)、求海岛B到灯塔C的距离;(2)、若这条船继续向正北航行,问什么时间小船与灯塔C的距离最短?

