山西省太原市杏花岭区2022-2023学年八年级上学期期中数学试卷

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个实数中，最大的数是（）

A、－3 B、－1 C、 $\sqrt{10}$ D、3

查看试题解析
2. 在 $\sqrt{1.5}$ ， $\sqrt{30}$ ， $\sqrt{\frac{1}{2}}$ ， $\sqrt{12}$ 中最简二次根式的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
3. 下列二次根式中，不能与 $\sqrt{3}$ 合并的是（　）

A、 $\sqrt{12}$ B、 $\sqrt{18}$ C、 $\sqrt{27}$ D、 $\sqrt{48}$

查看试题解析
4. 如图，作一个正方形，使其边长为单位长度，以表示数1的点为圆心，正方形对角线的长为半径画弧，交数轴于点A，则点A表示的数是（）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{3}$ C、 $1 - \sqrt{3}$ D、 $1 - \sqrt{2}$

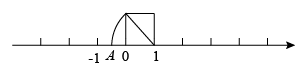查看试题解析
5. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）²＝21，小正方形的面积为5，则大正方形的面积为（）

A、13 B、14 C、15 D、16

查看试题解析
6. 下面哪个点不在函数 $y = - 2 x + 3$ 的图像上（）

A、（3，0） B、（0.5，2） C、（-5，13） D、（1，1）

查看试题解析
7. 对于一次函数 $y = \frac{1}{2} x - 3$ 的描述错误的是（）

A、y随x的增大而增大 B、图象与y轴的交点是 $(0 ， - 3)$ C、图象经过点 $(- 2 ， - 1)$ D、图象不经过第二象限

查看试题解析
8. 在同一坐标系中，函数y＝2kx与y＝x-k的图象大致是（）

A、 B、 C、 D、

查看试题解析
9. 如图1，动点P从矩形ABCD的顶点A出发，在边AB，BC上沿A→B→C的方向，以1cm/s的速度匀速运动到点C，△APC的面积 $S (c m^{2})$ 随运动时间t（s）变化的函数图象如图2所示，则AC的长是（）

A、3cm B、4cm C、5cm D、6cm

查看试题解析
10. 如图，在平面直角坐标系中，已知 $A (2 ， 0)$ ， $B (1 ， 3)$ ．在y轴上有一动点C，当△ABC的周长最小时，点C的坐标是（）

A、 $(0 ， 0)$ B、 $(0 ， - 2)$ C、 $(0 ， 2)$ D、 $(- 2 ， 0)$

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{4 - 2 x}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 4－ $\sqrt{15}$ 的倒数是．

查看试题解析
13. 若线段 $A B ∥ x$ 轴且 $A B = 3$ ，点A的坐标为 $(- 2 ， 1)$ ，则点B的坐标为．

查看试题解析
14. 如图，是一片树叶标本，将其放在平面直角坐标系中，表示叶片尖端A，B两点的坐标分别为（-3，3）（-1，0），则叶柄底部点C的坐标为．

查看试题解析
15. 甲、乙两车从A地出发，匀速驶向B地．甲车以 $80 k m / h$ 的速度行驶 $1 h$ 后，乙车才沿相同路线行驶，乙车先到达B地并停留 $1 h$ 后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离 $y (k m)$ 与乙车行驶时间 $x (h)$ 之间的函数关系如图所示．下列说法：①乙车的速度是 $120 k m / h$ ；② $m = 160$ ；③点H的坐标是 $(7 ， 85)$ ；④ $n = 7.4$ ，其中正确的有（填序号）．

查看试题解析

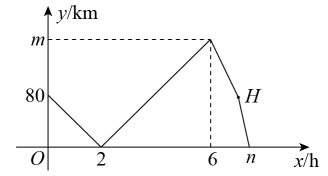
三、解答题

16. 计算题：

(1)、 $\sqrt{5} + (\sqrt{20} - \sqrt{45})$

(2)、 $3 \div \sqrt{3} \times \frac{1}{\sqrt{3}}$

(3)、 ${(3 - \sqrt{2})}^{2}$

(4)、 $(5 + 2 \sqrt{6}) (5 - 2 \sqrt{6})$

查看试题解析
17. 如图，在边长为1的小正方形所组成的网格上，每个小正方形的顶点都称为“格点”，△ABC的顶点都在格点上，用直尺完成下列作图：

(1)、作出△ABC关于直线MN的对称图形；

(2)、求△ABC的面积；

(3)、在直线MN上取一点P，使得AP＋CP最小（保留作图痕迹）

查看试题解析
18. 作出函数 $y = - 2 x + 4$ 的图象，并结合图象回答问题：

(1)、当 $y = - 3$ 时，；

(2)、图象与坐标轴的两个交点的坐标分别是；

(3)、图象与坐标轴围成的三角形的面积是；

(4)、当 $y < 0$ 时，x的取值范围是；
当 $y = 0$ 时，x的值是；
当 $y > 0$ 时，x的取值范围是；

(5)、若 $- 2 ≤ y ≤ 2$ 时，则x的取值范围是；

(6)、若 $- 2 \leq x \leq 2$ 时，则y的取值范围是．

查看试题解析
19. 某道路安装的护栏平面示意图如图所示，每根立柱宽为0.2米，立柱间距为3米．

(1)、设有x根立柱，护栏总长度为y米，请写出y与x之间的关系式．

(2)、当护栏的总长度为61米时，求出立柱的根数．

查看试题解析
20. 如图，5米长的一根木棒AB靠在墙上A点处，落地点为B，已知OB＝4米．现从O点处拉出一根铁丝OP（点P在线段AB上）来加固该木棒

(1)、在图中画出铁丝最短时的情形，并求出此时铁丝的长度

(2)、如果落地点B向墙角O处移动2米，则木棒上端A上移是少于2米，还是多于2米？
并说明理由

查看试题解析
21. 如图，已知直线 $y = 4 x - 6$ 与x轴交于点A，直线 $y = - 2 x - 2$ 与x轴交于点B，且这两条直线交于点C．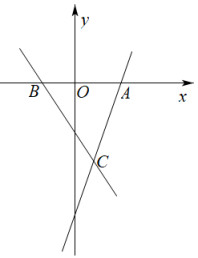

(1)、点A的坐标为，点B的坐标为；

(2)、这两条直线交点C的坐标为；

(3)、求出 $△ A B C$ 的面积．

查看试题解析
22. 如图，直线y＝ $\frac{4}{3}$ x+4与x轴、y轴分别交于点A和点B．

(1)、求A，B两点的坐标；

(2)、过B点作直线与x轴交于点P，若△ABP的面积为8，试求点P的坐标．

(3)、点M是OB上的一点，若将△ABM沿AM折叠，点B恰好落在x轴上的点B₁处，求
出点M的坐标．

(4)、点C在y轴上，连接AC，若△ABC是以AB为腰的等腰三角形，请直接写出点C的坐标．

查看试题解析
23. 倡导垃圾分类，共享绿色生活．为了对回收的垃圾进行更精准的分类，某机器人公司研发出A型和B型两款垃圾分拣机器人，每台A型、B型机器人每小时分栋垃圾分别为0.4吨和0.2吨．

(1)、某垃圾处理厂计划向机器人公司购进一批A型和B型垃圾分栋机器人，这批机器人每小时一共能分拣垃圾20吨．设购买A型机器人x台（ $10 \leq x \leq 35$ ），B型机器人y台，请求出y关于x的函数解析式；

(2)、机器人公司的报价如下表：
型号
原价
购买数量少于30台
购买数量不少于30台
A型
20万元/台
原价购买
每台打九折
B型
12万元/台
原价购买
每台打八折
在（1）的条件下，设购买走费用为w万元，问如何购买A型和B型机器人，使得购买总费用w最少？请说明理由．

查看试题解析

型号	原价	购买数量少于30台	购买数量不少于30台
A型	20万元/台	原价购买	每台打九折
B型	12万元/台	原价购买	每台打八折