山西省吕梁市交城县2022-2023学年八年级上学期期中考试数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点M的坐标为 $(- 2 ， 5)$ ，那么点M关于y轴的对称点N的坐标是（）

A、 $(- 2 ， - 5)$ B、 $(2 ， 5)$ C、 $(2 ， - 5)$ D、 $(5 ， - 2)$

查看试题解析
3. 若一个多边形的每一个外角都等于40°，则这个多边形的边数是（）

A、7 B、8 C、9 D、10

查看试题解析
4. 下列判断正确的是（）

A、有一条直角边对应相等的两个直角三角形全等 B、腰相等的两个等腰三角形全等 C、斜边相等的两个等腰直角三角形全等 D、有一个锐角对应相等的两个直角三角形全等

查看试题解析
5. 如图，点E， F在直线AC上，DF=BE， ∠AFD=∠CEB，下列条件中不能判断△ADF≌△CBE的是（）

A、∠D=∠B B、AD=CB C、AE=CF D、AD// BC

查看试题解析
6. 如图， $Δ A B C ≌ Δ A E F$ ，给出下列结论：① $A C = A F$ ；② $∠ F A B = ∠ E A B$ ；③ $E F = B C$ ；④ $∠ E A B = ∠ F A C$ ．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C，D，则下列结论错误的是（　　）

A、PC=PD B、∠CPD=∠DOP C、∠CPO=∠DPO D、OC=OD

查看试题解析
8. 如图，MN是线段AB的垂直平分线，C在MN外，且与A点在MN的同一侧，BC交MN于P点，则（）

A、BC>PC+AP B、BC<PC+AP C、BC=PC+AP D、BC≥PC+AP

查看试题解析
9. 如图，在四边形ABDC中，∠B＝∠D＝90°，∠BAC与∠ACD的平分线交于点O，且点O在线段BD上，BD＝4，则点O到边AC的距离是（）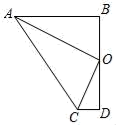

A、1 B、1.5 C、2 D、3

查看试题解析
10. 如图， $△ A B C$ 的面积为12，点D，E，F分别为 $B C ， A D ， C E$ 的中点，则阴影部分的面积为（）

A、2 B、3 C、4 D、6

查看试题解析

二、填空题

11. 正十二边形的内角和是．

查看试题解析
12. 在△ABC中，若AB=4，BC=2，且AC的长为偶数，则AC= ．

查看试题解析
13. 从一个多边形的一个顶点出发共可作10条对角线，则这个多边形共有对角线的条数为．

查看试题解析
14. 如图，在 $△ A B C$ 中， $A D$ 平分 $∠ B A C$ ， $A E ⊥ B C$ 于点E， $∠ B = 40 °$ ， $∠ D A E = 15 °$ ，则 $∠ C =$ °．

查看试题解析
15. 如图，线段AB=8cm，射线AN⊥AB，垂足为点A，点C是射线上一动点，分别以AC，BC为直角边作等腰直角三角形，得△ACD与△BCE，连接DE交射线AN于点M，则CM的长为．

查看试题解析

三、解答题

16. 如图，在四边形ABCD中，AB＝AD.在BC上求作一点P使△ABP≌△ADP.（要求：用尺规作图，不写作法，保留作图痕迹）

查看试题解析
17. 如图， $∠ A B C$ 的平分线与 $△ A B C$ 的外角 $∠ A C D$ 的平分线相交于点P．若 $∠ A = 80 °$ ，求 $∠ P$ 的度数．

查看试题解析
18. 如图，在直角坐标系中，A（﹣1，5），B（﹣3，0），C（﹣4，3）.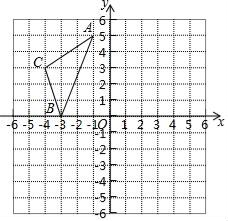

(1)、在图中作出△ABC关于y轴对称的图形△A₁B₁C₁；

(2)、写出点C₁的坐标；

(3)、求△ABC的面积.

查看试题解析
19. 如图， $A F$ 平分 $∠ B A C$ ，点P是 $A F$ 上任意一点，过点P向 $A B$ ， $A C$ 作垂线段 $P D$ ， $P E$ ，垂足分别为D，E，连接 $D E$ ．求证： $A F$ 垂直平分 $D E$ ．

查看试题解析
20. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 2 A C$ ．

(1)、按要求作图：作线段 $A B$ 的垂直平分线 $D E$ ，交 $B C$ 于点D，垂足为点E，连接 $A D$ （尺规作图，保留痕迹，不写作法）；

(2)、求证： $A D$ 平分 $∠ B A C$ ．

查看试题解析
21. 某产品的商标如图所示，O是线段AC、DB的交点，且AC=BD，AB=DC，小林认为图中的两个三角形全等，他的思考过程是：
∵ AC=DB，∠AOB=∠DOC，AB=DC，
∴ △ABO≌△DCO．
你认为小林的思考过程对吗？
如果正确，指出他用的是哪个判别三角形全等的方法；如果错误，写出你的思考过程

查看试题解析
22. 如图，在Rt△ABC中，∠BAC=90°，∠ABC=60°，AD，CE分别平分∠BAC，∠ACB．

(1)、求∠AOE得度数；

(2)、求证：AC=AE+CD．

查看试题解析
23. 综合与实践：
问题情境：已知 $O M$ 是 $∠ A O B$ 的平分线，P是射线 $O M$ 上的一点，点C，D分别在射线 $O A$ ， $O B$ 上，连接 $P C ， P D$ ．

(1)、初步探究：如图1，当 $P C ⊥ O A$ ， $P D ⊥ O B$ 时， $P C$ 与 $P D$ 的数量关系是；

(2)、深入探究：如图2，点C，D分别在射线 $O A$ ， $O B$ 上运动，且 $∠ A O B = 90 °$ ，当 $∠ C P D = 90 °$ 时， $P C$ 与 $P D$ 在（1）中的数量关系还成立吗？请说明理由；

(3)、拓展应用：如图3，如果点C在射线 $O A$ 上运动，且 $∠ A O B = 90 °$ ，当 $∠ C P D = 90 °$ 时，点D落在了射线 $O B$ 的反向延长线上，若点P到 $O B$ 的距离为3， $O D = 1$ ，求 $O C$ 的长（直接写出答案）．

查看试题解析