辽宁省沈阳市沈北新区2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 在平面直角坐标系中,下列坐标所对应的点位于第三象限的是( )A、(-1,2) B、(1,2) C、(2,-1) D、(-1,-3)2. 函数y=(k2-1)x+3是一次函数,则k的取值范围是( )A、k≠1 B、k≠-1 C、k≠±1 D、k为任意实数3. 如图,将边长为2的正方形OABC放在平面直角坐标系中,O是原点,点A的横坐标为1,则点C的坐标为( )
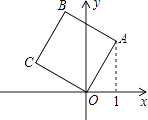 A、(﹣2,1) B、(﹣1,2) C、( ,﹣1) D、(﹣ ,1)4. 直角三角形两直角边分别为5cm和12cm,则其斜边的高为( )A、6cm B、8cm C、 cm D、 cm5. 已知等腰三角形的腰长为5,底边长为8,则它的面积为( )A、10 B、12 C、20 D、246. 的平方根是( )A、 B、 C、 D、7. 对于函数y=-x+3,下列结论正确的是( )A、它的图象与两坐标轴围成等腰直角三角形 B、它的图象经过第一、二、三象限 C、它的图象必经过点(-1,3) D、y的值随x值的增大而增大8. 若一个正数的两个平方根分别是2m-4与3m-1,则m的值是( )A、1 B、-1 C、-3 D、-3或19. 下列图象中,表示y是x的函数的个数有( )
A、(﹣2,1) B、(﹣1,2) C、( ,﹣1) D、(﹣ ,1)4. 直角三角形两直角边分别为5cm和12cm,则其斜边的高为( )A、6cm B、8cm C、 cm D、 cm5. 已知等腰三角形的腰长为5,底边长为8,则它的面积为( )A、10 B、12 C、20 D、246. 的平方根是( )A、 B、 C、 D、7. 对于函数y=-x+3,下列结论正确的是( )A、它的图象与两坐标轴围成等腰直角三角形 B、它的图象经过第一、二、三象限 C、它的图象必经过点(-1,3) D、y的值随x值的增大而增大8. 若一个正数的两个平方根分别是2m-4与3m-1,则m的值是( )A、1 B、-1 C、-3 D、-3或19. 下列图象中,表示y是x的函数的个数有( ) A、1个 B、2个 C、3个 D、4个10. 如图,已知一次函数 的图象为直线,则关于x的方程 的解为 ( )
A、1个 B、2个 C、3个 D、4个10. 如图,已知一次函数 的图象为直线,则关于x的方程 的解为 ( )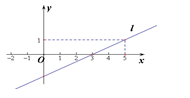 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在函数中,当时,y是x的正比例函数.12. 等边三角形的边长为6 cm,则它的高为 .13. 在平面直角坐标系内,已知点在第三象限的角平分线上,则点P的坐标为 .14. 一次函数的图象与x轴的交点为A,与y轴的交点为B,坐标原点为O,则的面积为 .15. 如图,根据图中的标注和作图痕迹可知,在数轴上的点A所表示的数为 .
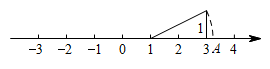 16. 如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为 .
16. 如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为 .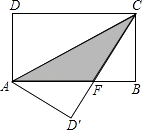
三、解答题
-
17. 计算:(1)、;(2)、;(3)、;(4)、 .18. 在由边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,四边形ABCD是格点四边形(顶点为网格线的交点).
 (1)、写出点A,B,C,D的坐标;
(1)、写出点A,B,C,D的坐标;
(2)、求四边形ABCD的面积.
19. 求下列各式中x的值:(1)、;(2)、 .20.(1)、设的小数部分为b,求的值;(2)、已知 , , 求的值.21. 如图,在四边形ABCD中,AB=AD=8cm,∠A=60°,∠ADC=150°,已知四边形ABCD的周长为32cm,求△BCD的面积. 22. 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米/秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
22. 如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米/秒的速度收绳,10秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号) 23. 如图,直线与x轴、y轴分别交于点B,C,点A的坐标为 , 是直线在第一象限内一个动点.
23. 如图,直线与x轴、y轴分别交于点B,C,点A的坐标为 , 是直线在第一象限内一个动点.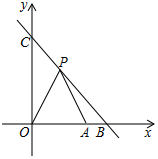 (1)、求的面积S与x的函数关系式,并写出自变量的x的取值范围;(2)、当的面积为24时,求点P的坐标.24. 已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm.
(1)、求的面积S与x的函数关系式,并写出自变量的x的取值范围;(2)、当的面积为24时,求点P的坐标.24. 已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm. (1)、求证:CD⊥AB;(2)、求该三角形的腰的长度.25. 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地米,小明登上山顶立即按原路匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程(米),(米)与小明出发的时间x(分)的函数关系如图所示.
(1)、求证:CD⊥AB;(2)、求该三角形的腰的长度.25. 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地米,小明登上山顶立即按原路匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程(米),(米)与小明出发的时间x(分)的函数关系如图所示. (1)、图中a= , b=;(2)、小明上山的速度米/分;小明下山的速度米/分;爸爸上山的速度米/分.(3)、小明的爸爸下山所用的时间 .26. 如图,直线 与x轴、y轴分别交于 两点, 于点M,点P为直线l上不与点 重合的一个动点.
(1)、图中a= , b=;(2)、小明上山的速度米/分;小明下山的速度米/分;爸爸上山的速度米/分.(3)、小明的爸爸下山所用的时间 .26. 如图,直线 与x轴、y轴分别交于 两点, 于点M,点P为直线l上不与点 重合的一个动点.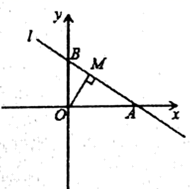 (1)、求线段 的长;(2)、当 的面积是6时,求点P的坐标;(3)、在y轴上是否存在点Q,使得以O、P、Q为顶点的三角形与 全等,若存在,请直接写出所有符合条件的点P的坐标,否则,说明理由.
(1)、求线段 的长;(2)、当 的面积是6时,求点P的坐标;(3)、在y轴上是否存在点Q,使得以O、P、Q为顶点的三角形与 全等,若存在,请直接写出所有符合条件的点P的坐标,否则,说明理由.