江西省南昌市十校联考2022-2023学年八年级上学期期中联考数学试卷
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个多边形的每个内角都等于135°,则这个多边形的边数为( )A、8 B、9 C、10 D、113. 等腰三角形一腰上的高与另一腰上的夹角为 , 则顶角的度数为( )A、 B、 C、或 D、或4. 如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( )
2. 一个多边形的每个内角都等于135°,则这个多边形的边数为( )A、8 B、9 C、10 D、113. 等腰三角形一腰上的高与另一腰上的夹角为 , 则顶角的度数为( )A、 B、 C、或 D、或4. 如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( ) A、AD=AE B、AB=AC C、BE=CD D、∠AEB=∠ADC5. 如图, , , B点在的垂直平分线上,若 , 则为( )
A、AD=AE B、AB=AC C、BE=CD D、∠AEB=∠ADC5. 如图, , , B点在的垂直平分线上,若 , 则为( ) A、4 B、6 C、8 D、106. 如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )个.
A、4 B、6 C、8 D、106. 如图,在2×2的方格纸中有一个以格点为顶点的△ABC,则与△ABC成轴对称且以格点为顶点三角形共有( )个. A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题
-
7. 点关于y轴对称的点的坐标是 .8. 若等腰三角形的两边长分别为3cm和8cm,则它的周长是.9. 如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2= .
 10. 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为 .
10. 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为 . 11. 如图,在中,H是高和的交点,且 , 已知 , 则的长为 .
11. 如图,在中,H是高和的交点,且 , 已知 , 则的长为 . 12. 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是(填序号)
12. 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④AE=EC,其中正确的是(填序号)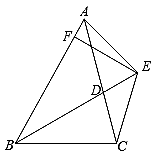
三、解答题
-
13. 在中, , .(1)、求 , , 的度数;(2)、按边分类,属于三角形,按角分类,属于三角形.14. 如图,点在同一直线上, , , . 求证:
 (1)、;(2)、 .15. 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)、;(2)、 .15. 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题: (1)、画出格点(顶点均在格点上)关于直线对称的;(2)、在上找出点Q,使最短.16. 在△ABC中,AB=AC,AC上的中线BD把三角形的周长分为15㎝和30㎝的两个部分,求:三角形的三边长.17. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.
(1)、画出格点(顶点均在格点上)关于直线对称的;(2)、在上找出点Q,使最短.16. 在△ABC中,AB=AC,AC上的中线BD把三角形的周长分为15㎝和30㎝的两个部分,求:三角形的三边长.17. 如图,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F.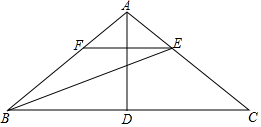 (1)、若∠C=36°,求∠BAD的度数;(2)、求证:FB=FE.18. 如图Rt△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于D,BF平分∠ABC,交AD于E,交AC于F.
(1)、若∠C=36°,求∠BAD的度数;(2)、求证:FB=FE.18. 如图Rt△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于D,BF平分∠ABC,交AD于E,交AC于F. (1)、求证:△AEF是等边三角形;(2)、求证:BE=EF.19. 已知: , 垂足分别为D,E.
(1)、求证:△AEF是等边三角形;(2)、求证:BE=EF.19. 已知: , 垂足分别为D,E. (1)、如图1,①线段和的数量关系是 ;
(1)、如图1,①线段和的数量关系是 ;②请写出线段之间的数量关系并证明;
(2)、如图2,请写出线段之间的数量关系并证明20. 小明在学习完“等腰三角形底边上的高线、中线及顶角平分线重合”,继续探索,他猜想“如果三角形的一条角平分线是这个角对边上的中线,那么这个三角形是等腰三角形”并进行了证明. (1)、请根据以上命题和图形写出已知和求证:
(1)、请根据以上命题和图形写出已知和求证:已知: ,
求证: .
(2)、请证明以上命题.21. 如图,在中, , , , , , 动点E以的速度从A点向F点运动,动点G以的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t. (1)、求证:;(2)、当t取何值时,与全等.22. 如图,在中, , 点D是直线上一点(不与B,C重合),以为一边在的右侧作 , 使 , , 连结 .
(1)、求证:;(2)、当t取何值时,与全等.22. 如图,在中, , 点D是直线上一点(不与B,C重合),以为一边在的右侧作 , 使 , , 连结 .
 (1)、如图1,当点D在线段BC上时,如果 , 则;(2)、设 , .
(1)、如图1,当点D在线段BC上时,如果 , 则;(2)、设 , .①如图2,当点D在线段BC上移动时, , 之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动时, , 之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论.
23. 【阅读理解】如图1.在中,若 , , 求边上的中线的取值范围.解决此问题可以用如下方法:延长到点E,使 , 再连接(或将绕着点D逆时针旋转得到),把 , , 集中在中, (1)、利用三角形的三边关系直接写出中线的取值范围是;(2)、【问题解决】如图2,在中,D是边上的中点,于点D,交于点E,交于点F,连接 , 求证:;(3)、【问题拓展】如图3,在中, , D为边的中点,求证: .
(1)、利用三角形的三边关系直接写出中线的取值范围是;(2)、【问题解决】如图2,在中,D是边上的中点,于点D,交于点E,交于点F,连接 , 求证:;(3)、【问题拓展】如图3,在中, , D为边的中点,求证: .