江西省赣州市定南县2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 下列交通标志是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三根小木棒能构成三角形的是( )A、2cm,3cm,5cm B、7cm,4cm,2cm C、3cm,4cm,8cm D、3cm,3cm,4cm3. 如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则∠1+∠2等于( )
2. 下列长度的三根小木棒能构成三角形的是( )A、2cm,3cm,5cm B、7cm,4cm,2cm C、3cm,4cm,8cm D、3cm,3cm,4cm3. 如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则∠1+∠2等于( ) A、60° B、75° C、90° D、105°4. 下列四个图形中,线段BE是△ABC的高的是( )A、
A、60° B、75° C、90° D、105°4. 下列四个图形中,线段BE是△ABC的高的是( )A、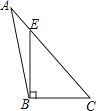 B、
B、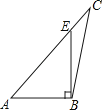 C、
C、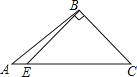 D、
D、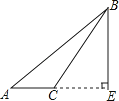 5. 如图,△ABC 中,于点D,根据“”判定 , 还需添加条件( )
5. 如图,△ABC 中,于点D,根据“”判定 , 还需添加条件( ) A、 B、 C、 D、6. 如图,在等腰直角中, , , 点F为AB中点,点D、E分别在边AC、CB上运动,且始终保持 , 在此运动变化过程中,下列结论:①;②是等腰直角三角形;③;④四边形的面积始终保持不变;其中正确结论有( )
A、 B、 C、 D、6. 如图,在等腰直角中, , , 点F为AB中点,点D、E分别在边AC、CB上运动,且始终保持 , 在此运动变化过程中,下列结论:①;②是等腰直角三角形;③;④四边形的面积始终保持不变;其中正确结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 如图是一个轴对称图形,若 , 则 .
 8. 如图,图中显示的是从镜子中看到背后墙上的电子钟读数,由此你可以推断这时的实际时间是.
8. 如图,图中显示的是从镜子中看到背后墙上的电子钟读数,由此你可以推断这时的实际时间是. 9. 若正多边形的一个外角是60°,则这个正多边形的是边形.10. 如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2 , 则△BDE的面积为.
9. 若正多边形的一个外角是60°,则这个正多边形的是边形.10. 如图,在△ABC中,D、E分别是BC、AD的中点,△ABC的面积为6cm2 , 则△BDE的面积为.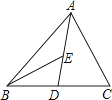 11. 如图,点A,D,C在同一条直线上,且 , 若 , 则的度数为 .
11. 如图,点A,D,C在同一条直线上,且 , 若 , 则的度数为 . 12. 如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
12. 如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
三、解答题
-
13.(1)、如图,已知 , 求证;
 (2)、一个多边形的内角和是 , 求多边形的边数.14. 在中, , 求的度数.15. 如图,在△ABC与△DCB中,AB=DC,AC=BD,AC与BD交于M.求证:BM=CM.
(2)、一个多边形的内角和是 , 求多边形的边数.14. 在中, , 求的度数.15. 如图,在△ABC与△DCB中,AB=DC,AC=BD,AC与BD交于M.求证:BM=CM.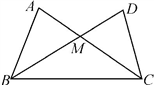 16. 请仅用无刻度的直尺,根据下列条件分别在图1和图2中画出的垂直平分线.(保留作图痕迹,不写作法)
16. 请仅用无刻度的直尺,根据下列条件分别在图1和图2中画出的垂直平分线.(保留作图痕迹,不写作法) (1)、如图1,是以为底边的等腰三角形,点D为内一点,;(2)、如图2, , E,F分别为 , 的中点.17. 如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF.
(1)、如图1,是以为底边的等腰三角形,点D为内一点,;(2)、如图2, , E,F分别为 , 的中点.17. 如图所示,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G,求证:AD垂直平分EF. 18. 如图,一个四边形纸片ABCD, ,把纸片按如图所示折叠,使点B落在AD边上的 点,AE是折痕.
18. 如图,一个四边形纸片ABCD, ,把纸片按如图所示折叠,使点B落在AD边上的 点,AE是折痕. (1)、判断 与DC的位置关系,并说明理由;(2)、如果 ,求 的度数.19. 在平面直角坐标系中,点 , 点 .(1)、若点A在第一象限的角平分线上,求a的值;(2)、若点A与点B关于x轴对称,求的值.20. 如图,在边长为1个单位长度的小正方组成的网格中,按要求画出△A1B1C1与△A2B2C2.
(1)、判断 与DC的位置关系,并说明理由;(2)、如果 ,求 的度数.19. 在平面直角坐标系中,点 , 点 .(1)、若点A在第一象限的角平分线上,求a的值;(2)、若点A与点B关于x轴对称,求的值.20. 如图,在边长为1个单位长度的小正方组成的网格中,按要求画出△A1B1C1与△A2B2C2.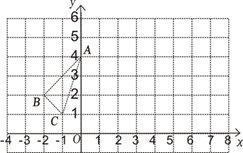
( 1 )作出△ABC关于y轴对称的△A1B1C1;
( 2 )将△ABC向右平移6个单位,作出平移后的△A2B2C2;
( 3 )观察△A1B1C1和△A2B2C2 , 他们是否关于某直线对称?若是,请用粗线条画出对称轴.
21. 如图, , 相交于点O,且 , . (1)、求证:;(2)、若在直线上截取 , 求证: .22. 如图,在△中,点分别在边上,与交于点O,给出下列三个条件:①∠=∠;②;③ .
(1)、求证:;(2)、若在直线上截取 , 求证: .22. 如图,在△中,点分别在边上,与交于点O,给出下列三个条件:①∠=∠;②;③ .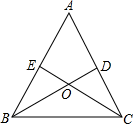 (1)、上述三个条件中,由哪两个条件可以判定是等腰三角形?(用序号写出所有成立的情形)(2)、请选择(1)中的一种情形,写出证明过程.23. 问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板的两条直角边上,点A与点P在直线的同侧,若点P在内部,试问 , 与的大小是否满足某种确定的数量关系?
(1)、上述三个条件中,由哪两个条件可以判定是等腰三角形?(用序号写出所有成立的情形)(2)、请选择(1)中的一种情形,写出证明过程.23. 问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板的两条直角边上,点A与点P在直线的同侧,若点P在内部,试问 , 与的大小是否满足某种确定的数量关系?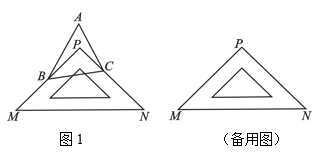 (1)、特殊探究:若 , 则度,度,度;(2)、类比探索:请猜想与的关系,并说明理由;(3)、类比延伸:改变点A的位置,使点P在外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出 , 与满足的数量关系式.
(1)、特殊探究:若 , 则度,度,度;(2)、类比探索:请猜想与的关系,并说明理由;(3)、类比延伸:改变点A的位置,使点P在外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出 , 与满足的数量关系式.