广东省佛山市南海区西樵镇2022-2023学年八年级上学期期中考数学试题
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 下列实数中是无理数的是( )A、0.38 B、 C、 D、2. 在平面直角坐标系中,点 的位置在A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各组数分别为一个三角形三边的长,其中能构成直角三角形的一组是( )A、1, , 2 B、2,3,4 C、4,5,6 D、1,3,24. 下列四点在函数 的图象上的点是( )A、 B、 C、 D、5. 一矩形的长为 ,宽为 ,则该矩形的面积为( )A、 B、3 C、 D、6. 一个正方体的体积是100,估计它的棱长的大小在( )A、3与4之间 B、4与5之间 C、5与6之间 D、6与7之间7. 如图,圆柱的底面周长是24,高是5,—只在A点的蚂蚁沿侧面爬行,想吃到B点的食物,需要爬行的最短路径是( )
 A、9 B、13 C、14 D、8. 将△ABC的三个顶点坐标的横坐标都乘以-1,并保持纵坐标不变,则所得图形与原图形的关系是( )
A、9 B、13 C、14 D、8. 将△ABC的三个顶点坐标的横坐标都乘以-1,并保持纵坐标不变,则所得图形与原图形的关系是( ) A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、将原图形沿x轴的负方向平移了1个单位9. 下列结论正确的是( )A、有理数与数轴上的点一一对应 B、二次根式有意义条件是 C、立方根等于它本身是 D、如果 , 那么10. 关于函数 , 下列结论正确的是( )A、图象必经过点 B、y随x的增大而增大 C、当时, D、图象经过第一、二、三象限
A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、将原图形沿x轴的负方向平移了1个单位9. 下列结论正确的是( )A、有理数与数轴上的点一一对应 B、二次根式有意义条件是 C、立方根等于它本身是 D、如果 , 那么10. 关于函数 , 下列结论正确的是( )A、图象必经过点 B、y随x的增大而增大 C、当时, D、图象经过第一、二、三象限二、填空题
-
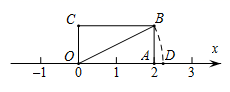
11. -8的立方根是.12. 比较大小:(填“>”或“<”或“=”) .13. 如图,在矩形中, , , , 数轴上点所表示的数是 .
 14. 如图,已知AD//BC , BD平分∠ABC , ∠A=112°,且BD⊥CD , 则∠ADC= .
14. 如图,已知AD//BC , BD平分∠ABC , ∠A=112°,且BD⊥CD , 则∠ADC= . 15. 如图,已知 是腰长为1的等腰直角三角形,以 的斜边AC为直角边,画第二个等腰 ,再以 的斜边AD为直角边,画第三个等腰 ,……依此类推,则第2021个等腰直角三角形的斜边长是 .
15. 如图,已知 是腰长为1的等腰直角三角形,以 的斜边AC为直角边,画第二个等腰 ,再以 的斜边AD为直角边,画第三个等腰 ,……依此类推,则第2021个等腰直角三角形的斜边长是 .
三、解答题
-
16. +(+1)(-1)17. 如图,在 中, , , ,点 从点 出发,以每秒 的速度向点 运动,连接 ,设运动时间为 秒 .
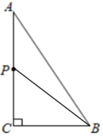 (1)、 ;(2)、当 时,求 的值.18. 已知与x成正比例关系,且当时, .
(1)、 ;(2)、当 时,求 的值.18. 已知与x成正比例关系,且当时, . (1)、求y与x之间的函数关系式;(2)、请在下面直角坐标系中,画出这个函数的图象.19. 如图,点、、的坐标分别是、、 .
(1)、求y与x之间的函数关系式;(2)、请在下面直角坐标系中,画出这个函数的图象.19. 如图,点、、的坐标分别是、、 . (1)、判断的形状,并说明理由;(2)、点是轴上的一动点,求出使得的值最小时点的坐标.20. 如图是规格为的正方形网格,请在所给网格中按下列要求操作:
(1)、判断的形状,并说明理由;(2)、点是轴上的一动点,求出使得的值最小时点的坐标.20. 如图是规格为的正方形网格,请在所给网格中按下列要求操作: (1)、在网格(每个小正方形边长为1)中建立平面直角坐标系,使A点坐标为 , B点坐标为;(2)、在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是;(3)、画出关于y轴对称的 .21. 如图,在平面直角坐标系中,轴,轴, , 点B的坐标为 . 将沿AC折叠得到 , 点B落在点D的位置,交y轴于点E,
(1)、在网格(每个小正方形边长为1)中建立平面直角坐标系,使A点坐标为 , B点坐标为;(2)、在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是;(3)、画出关于y轴对称的 .21. 如图,在平面直角坐标系中,轴,轴, , 点B的坐标为 . 将沿AC折叠得到 , 点B落在点D的位置,交y轴于点E, (1)、求点D的坐标.(2)、求经过点A、D的直线的解析式.22. 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角处
(1)、求点D的坐标.(2)、求经过点A、D的直线的解析式.22. 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角处 (1)、请你在下面网格(每个小正方形边长为1)中,画出蚂蚁能够最快到达目的地的可能路径;(2)、当 , , 时,求蚂蚁爬过的最短路径的长;(3)、我们发现,“用不同的方式表示同一图形的面积”可以解决计算线段的有关问题,这种方法称为“面积法”.请“面积法”求点到最短路径的距离.23. 如图1,直线交x轴于点A,交y轴于点B,点C在上,且 .
(1)、请你在下面网格(每个小正方形边长为1)中,画出蚂蚁能够最快到达目的地的可能路径;(2)、当 , , 时,求蚂蚁爬过的最短路径的长;(3)、我们发现,“用不同的方式表示同一图形的面积”可以解决计算线段的有关问题,这种方法称为“面积法”.请“面积法”求点到最短路径的距离.23. 如图1,直线交x轴于点A,交y轴于点B,点C在上,且 . (1)、直接写出点C的坐标为;(2)、P为x轴负半轴上一点,且 , 连接 , 设的面积为S,直接写出S与m的函数关系式;(3)、在(2)的条件下,过点B作 , 交x轴于点D,若 , 求点D的坐标.
(1)、直接写出点C的坐标为;(2)、P为x轴负半轴上一点,且 , 连接 , 设的面积为S,直接写出S与m的函数关系式;(3)、在(2)的条件下,过点B作 , 交x轴于点D,若 , 求点D的坐标.