北京市通州区2022-2023学年八年级上学期期中考试数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 若代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则 $x$ 的取值范围是 $($ $)$

A、x<1 B、x≤1 C、x>1 D、x≥1

查看试题解析
2. 下列分式中是最简分式的是（）

A、 $\frac{2 x}{x^{2} + 1}$ B、 $\frac{4}{2 x}$ C、 $\frac{x - 1}{x^{2} - 1}$ D、 $\frac{1 - x}{x - 1}$

查看试题解析
3. 下列四个等式：① $\sqrt{(- 4)^{2}} = 4$ ；②（- $\sqrt{4}$ ）²＝16；③（ $\sqrt{4}$ ）²＝4；④ $\sqrt{(- 4)^{2}} = - 4$ ．正确的是（　　）

A、①② B、③④ C、②④ D、①③

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$ C、 $\sqrt{3} \times \sqrt{2} = 6$ D、 $\sqrt{8} \div \sqrt{2} = 4$

查看试题解析
5. 下列等式成立的是（）

A、 $\frac{1}{a} + \frac{2}{b} = \frac{3}{a + b}$ B、 $\frac{a b}{a b - b^{2}} = \frac{a}{a - b}$ C、 $\frac{2}{2 a + b} = \frac{1}{a + b}$ D、 $\frac{a}{- a + b} = - \frac{a}{a + b}$

查看试题解析
6. 小东一家自驾车去某地旅行，手机导航系统推荐了两条线路，线路一全程75km，线路二全程90km，汽车在线路二上行驶的平均时速是线路一上车速的1.8倍，线路二的用时预计比线路一用时少半小时，如果设汽车在线路一上行驶的平均速度为xkm/h，则下面所列方程正确的是（）

A、 $\frac{75}{x} = \frac{90}{1.8 x} + \frac{1}{2}$ B、 $\frac{75}{x} = \frac{90}{1.8 x} - \frac{1}{2}$ C、 $\frac{75}{1.8 x} = \frac{90}{x} + \frac{1}{2}$ D、 $\frac{75}{1.8 x} = \frac{90}{x} - \frac{1}{2}$

查看试题解析
7. 已知n是一个正整数，且 $\sqrt{24 n}$ 是整数，那么n的最小值是（）

A、6 B、36 C、3 D、2

查看试题解析
8. 若 $x y = - 6$ ，其中 $x > y$ ，则下列分式的值一定比 $\frac{y}{x}$ 的值大的是（）

A、 $\frac{3 y}{3 x}$ B、 $\frac{3 y}{x}$ C、 $- \frac{3}{x}$ D、 $\frac{y + 3}{x}$

查看试题解析

二、填空题

9. 3的算术平方根是．

查看试题解析
10. 若分式 $\frac{x - 1}{x + 2}$ 的值为0，则x的值为．

查看试题解析
11. 分式 $\frac{3}{2 b c} ， \frac{2}{5 c^{2}}$ 的最简公分母是．

查看试题解析
12. 写出一个比2大且比3小的无理数：．

查看试题解析
13. ① $\frac{3 a}{5 x y} = \frac{()}{10 a x y} ， (a \neq 0)$ ② $\frac{a + 2}{a^{2} - 4} = \frac{1}{()}$

查看试题解析
14. 若 $\sqrt{{(1 - a)}^{2}} = a - 1$ ，则a的取值范围是．

查看试题解析
15. 某种弹簧秤原来的长度为l，悬挂重物后的长度L可以用公式 $L = l + \frac{m}{k}$ 表示，其中m是悬挂物的质量，k是常数，则m= ．（用 $L ， l ， k$ 表示）

查看试题解析
16. 利用平方与开平方互为逆运算的关系，可以将某些无理数进行如下操作：例如： $a = \sqrt{3} + 1$ 时，移项得 $a - 1 = \sqrt{3}$ ，两边平方得 $(a - 1)^{2} = (\sqrt{3})^{2}$ ，所以 $a^{2} - 2 a + 1 = 3$ ，即得到整系数方程： $a^{2} - 2 a - 2 = 0$ ．仿照上述操作方法，完成下面的问题：当 $a = \frac{\sqrt{5} - 1}{2}$ 时，①得到的整系数方程为；②计算： $a^{3} - 2 a + 2025 =$ ．

查看试题解析

三、解答题

17. 计算： $(1 - π)^{0} + | - \sqrt{2} | + \sqrt[3]{27} - \sqrt{8}$ ．

查看试题解析
18. 计算： $4 a b^{2} \div {(\frac{- b}{a})}^{3}$ ．

查看试题解析
19. 计算： $\frac{2 x}{x - y} - \frac{2 y}{x - y}$ ．

查看试题解析
20. 计算： $3 \sqrt{20} - \sqrt{45} + \sqrt{\frac{1}{5}}$ ．

查看试题解析
21. 计算： $(\sqrt{3} + 1) (\sqrt{3} - 1) - (\sqrt{2} - 1)^{2}$ ．

查看试题解析
22. 解方程： $\frac{x}{x - 1}$ ＋ $\frac{1}{x}$ ＝1．

查看试题解析
23. 解方程 $\frac{2 x}{x - 2} = 1 -$ $\frac{1}{2 - x}$

查看试题解析
24. 先化简，再求值： $\frac{x^{2} + x}{x^{2} - 2 x + 1} \div (\frac{2}{x - 1} - \frac{1}{x})$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
25. 已知： $\sqrt{x - y} = 1$ ， ${(x + 2 y)}^{3} = 64$ ，求代数式 $\frac{x + y}{x^{2} + y^{2}}$ 的值.

查看试题解析
26. 如图为 $4 \times 4$ 方格，每个小正方形的边长都为1．

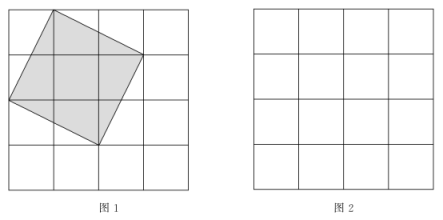(1)、图1中阴影正方形的面积为，边长为；

(2)、请在图2中画出一个与图1中阴影部分面积不相等的正方形，并求出所画正方形的边长．要求所画正方形满足以下条件：①正方形的边长为无理数 ②正方形的四个顶点均在网格格点处．

查看试题解析

27. 晨晨家近期准备换车，看中了价格相同的两款国产车．

燃油车	新能源车
油箱容积： $40$ 升	电池电量： $60$ 千瓦时
油价： $9$ 元/升	电价： $0.6$ 元/千瓦时
续航里程：a千米	续航里程：a千米
每千米行驶费用： $\frac{40 \times 9}{a}$ 元	每千米行驶费用：____元

注：续航里程是指在最大的能源储备下可连续行驶的总里程．

(1)、用含a的代数式表示新能源车的每千米行驶费用；

(2)、若燃油车的每千米行驶费用比新能源车多0.54元．

①分别求出这两款车的每千米行驶费用．

②若燃油车和新能源车每年的其它费用分别为4800元和7500元．问：每年行驶里程在什么范围时，买新能源车的年费用更低？（年费用=年行驶费用+年其它费用）

查看试题解析

28. 根据学习“数与式”的经验，通过由“特殊到一般”的方法探究下面二次根式的运算规律．以下是探究过程，请补充完整．

(1)、具体运算，发现规律．
特例1． $\sqrt{1 + 3} = 2$ ．特例2． $\sqrt{1 + \frac{5}{4}} = \frac{3}{2}$ ，特例3． $\sqrt{1 + \frac{7}{9}} = \frac{4}{3}$ ，特例4． $\sqrt{1 + \frac{9}{16}} = \frac{5}{4}$ ，
特例5．．

(2)、观察、归纳，得出猜想．
如果n为正整数，用含n的式子表示上述的运算规律为：．

(3)、证明你的猜想．

查看试题解析
29. 阅读理解
材料1：为了研究分式 $\frac{1}{x}$ 与其分母x的数量变化关系，小明制作了表格，并得到如下数据：
x
…
$- 4$
$- 3$
$- 2$
$- 1$
0
$1$
$2$
$3$
$4$
…
$\frac{1}{x}$
…
$- 0.25$
$- 0 . \dot{3}$
$- 0.5$
$- 1$
无意义
$1$
$0.5$
$0 . \dot{3}$
$0.25$ .
…
从表格数据观察，当 $x > 0$ 时，随着x的增大， $\frac{1}{x}$ 的值随之减小，若x无限增大，则 $\frac{1}{x}$ 无限接近于0；
当 $x < 0$ 时，随着x的增大， $\frac{1}{x}$ 的值也随之减小．
材料2：在分子、分母都是整式的情况下，如果分子的次数低于分母的次数，称这样的分式为真分式．如果分子的次数不低于分母的次数，称这样的分式为假分式．
任何一个假分式都可以化为一个整式与一个真分式的和．
例如：
$\frac{x + 1}{x - 4} = \frac{(x - 4) + 5}{x - 4} = \frac{x - 4}{x - 4} + \frac{5}{x - 4} = 1 + \frac{5}{x - 4}$
根据上述材料完成下列问题：

(1)、当 $x > 0$ 时，随着x的增大， $1 + \frac{1}{x}$ 的值（增大或减小）；
当 $x < 0$ 时，随着x的增大， $\frac{x + 2}{x}$ 的值（增大或减小）；

(2)、当 $x > 1$ 时，随着x的增大， $\frac{3 x + 1}{x - 1}$ 的值无限接近一个数，请求出这个数；

(3)、当 $0 < x < 2$ 时，请直接写出代数式 $\frac{2 x - 1}{x - 3}$ 值的范围．

查看试题解析

x	…	$- 4$	$- 3$	$- 2$	$- 1$	0	$1$	$2$	$3$	$4$	…
$\frac{1}{x}$	…	$- 0.25$	$- 0 . \dot{3}$	$- 0.5$	$- 1$	无意义	$1$	$0.5$	$0 . \dot{3}$	$0.25$ .	…