安徽省蚌埠市蚌山区2022-2023学年八年级上学期11月期中数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点(2，-1)所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 一本笔记本5元，买x本共付y元，则5和y分别是（）

A、常量，常量 B、变量，变量 C、常量，变量 D、变量，常量

查看试题解析
3. 在平面直角坐标系中，将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是（）

A、（﹣1，1） B、（﹣1，﹣2） C、（﹣1，2） D、（1，2）

查看试题解析
4. 一次函数 $y = k x - 2 k$ 的图象经过点 $A$ ，且 $y$ 随 $x$ 的增大而增大，则点 $A$ 的坐标可以是（）

A、 $(1 ， 1)$ B、 $(- 1 ， 3)$ C、 $(0 ， - 1)$ D、 $(3 ， - 1)$

查看试题解析
5. 若一个三角形的两边长分别为5和8，则第三边长可能是（）

A、14 B、10 C、3 D、2

查看试题解析
6. 在 $△ A B C$ 中， $∠ A = \frac{1}{2} ∠ B = \frac{1}{2} ∠ C$ ，则 $△ A B C$ 是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形

查看试题解析
7. 下列命题中，为真命题的是（　　）

A、两个锐角之和一定为钝角 B、相等的两个角是对顶角 C、同位角相等 D、垂线段最短

查看试题解析
8. 如图，在△ABC中，已知点D，E，F分别是BC，AD，CE的中点，且S_△ABC=4，S_△BEF=（）

A、2 B、1 C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
9. 如图所示，一次函数 $y = k x + b$ （k，b是常数 $k \neq 0$ ）与正比例函数 $y = m x$ （m是常数， $m \neq 0$ ）的图像相交于点 $M （ 1 ， 2 ）$ ，下列判断错误的是（）

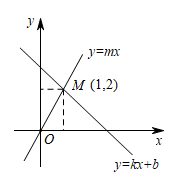A、关于x的方程 $m x = k x + b$ 的解是 $x = 1$ B、关于x的不等式 $m x < k x + b$ 的解集是 $x > 1$ C、当 $x < 0$ 时，函数 $y = k x + b$ 的值比函数 $y = m x$ 的值大 D、关于x，y的方程组 ${\begin{array}{l} y - m x = 0 \\ y - k x - b \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$

查看试题解析
10. 在平面直角坐标系中，已知A，B，C，D四点的坐标依次为（0，0），（6，2），（8，8），（2，6），若一次函数y＝mx﹣6m+2（m≠0）图象将四边形ABCD的面积分成1：3两部分，则m的值为（）

A、﹣4 B、 $- \frac{1}{5}$ ，﹣5 C、 $- \frac{1}{5}$ D、 $- \frac{1}{4}$ ，﹣4

查看试题解析

二、填空题

11. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 已知△A′B′O′是由△ABO平移得到的，点A的坐标为（-1，2），它的对应点A'的坐标为（3，4），△ABO内任意一点P（a，b）平移后的对应点P'的坐标为．

查看试题解析
13. 如图，直线 $l_{1} ： y = x + 1$ 与直线 $l_{2} ： y = m x + n$ 相交于点 $P (1 ， b)$ ，则关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} y = x + 1 \\ y = m x + n \end{array}$ 的解为．

查看试题解析
14. 探究与发现：如图，在 $△ A B C$ 中， $∠ B = ∠ C = 45 °$ ，点D在 $B C$ 边上，点E在 $A C$ 边上，且 $∠ A D E = ∠ A E D$ ，连接 $D E$ ．

(1)、当 $∠ B A D = 60 °$ 时，求 $∠ C D E =$ ．

(2)、当点D在 $B C$ (点 $B ， C$ 除外)边上运动时，试猜想 $∠ B A D$ 与 $∠ C D E$ 的数量关系为．

查看试题解析

三、解答题

15. 已知 $△ A B C$ 在平面直角坐标系中的位置如图所示．将 $△ A B C$ 向右平移6个单位长度，再向下平移6个单位长度得到 $△ A_{1} B_{1} C_{1} . ($ 图中每个小方格边长均为1个单位长度 $)$ ．

(1)、在图中画出平移后的 $△ A_{1} B_{1} C_{1}$ ；

(2)、直接写出 $△ A_{1} B_{1} C_{1}$ 各顶点的坐标．

查看试题解析
16. 在平面直角坐标系 $x O y$ 中，直线 $y = 2 x + 1$ 与 $x$ 轴交于点A，与y轴交于点B．求点 $A ， B$ 的坐标．

查看试题解析
17. 已知函数 $y = (m - 10) x + 1 - 2 m$ .

(1)、当m为何值时，这个函数是一次函数？

(2)、当m为何值时，这个函数是正比例函数？

查看试题解析
18. 已知 $y + 3$ 与x成正比例，当 $x = 2$ 时， $y = 7$ ．

(1)、求y与x的函数表达式；

(2)、当 $x = - \frac{1}{2}$ 时，求y的值．

查看试题解析
19. 如图， $l_{1}$ ， $l_{2}$ 分别表示两个一次函数的图象，它们相交于点P．

(1)、求出两条直线的函数关系式

(2)、点P的坐标可看作是哪个二元一次方程组的解．

查看试题解析
20. 如图，在△ABC中，AD，AE分别是△ABC的高和角平分线，若∠B=30°，∠C=50°．

(1)、求∠DAE的度数；

(2)、试写出 ∠DAE与∠C-∠B有何关系? 关系为：．

查看试题解析
21. 已知a、b、c是△ABC的三边长，a=4，b=6，设三角形的周长是x．

(1)、直接写出c及x的取值范围；

(2)、若x是小于18的偶数，①求c的长；
②判断△ABC的形状．

查看试题解析
22. 如图，△ABC中，D为BC上一点，∠C＝∠BAD ， △ABC的角平分线BE交AD于点F ．

(1)、求证：∠AEF＝∠AFE；

(2)、G为BC上一点，当FE平分∠AFG且∠C＝30°时，求∠CGF的度数．

查看试题解析
23. 已知一次函数 $y_{1} = a x + b$ 的图象交x轴和y轴于点B和D；另一个一次函数 $y_{2} = b x + a$ 的图象交x轴和y轴于点C和E，且两个函数的图象交于点 $A (1 ， 4)$

(1)、当a，b为何值时， $y_{1}$ 和 $y_{2}$ 的图象重合；

(2)、当 $0 < a < 4$ ，且在 $x < 1$ 时，则 $y_{1} > y_{2}$ 成立，求b的取值范围；

(3)、当 $△ A B C$ 的面积为 $\frac{16}{3}$ 时，求线段 $D E$ 的长．

查看试题解析