天津市津南区2022-2023学年九年级上学期11月期中考试数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 方程5x²－1＝4x化成一般形式后，二次项系数为正，其中一次项系数，常数项分别是（）

A、4，－1 B、4，1 C、－4，－1 D、－4，1

查看试题解析
2. 一元二次方程 $x^{2} - 2 x + 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
3. 用配方法解方程 $x^{2} - 6 x + 8 = 0$ 时，方程可变形为（）

A、 ${(x - 3)}^{2} = 1$ B、 ${(x - 3)}^{2} = - 1$ C、 ${(x + 3)}^{2} = 1$ D、 ${(x + 3)}^{2} = - 1$

查看试题解析
4. 已知x₁、x₂是一元二次方程2x²﹣4x+1＝0的两个实数根，则x₁•x₂等于（）

A、﹣2 B、﹣ $\frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
5. 已知关于x的一元二次方程kx²﹣2x+3＝0有两个不相等的实数根，则k的取值范围是（）

A、k＜ $\frac{1}{3}$ B、k＞﹣ $\frac{1}{3}$ C、k＞﹣ $\frac{1}{3}$ 且k≠0 D、k＜ $\frac{1}{3}$ 且k≠0

查看试题解析
6. 抛物线 $y = 2 (x - 3)^{2} + 4$ 的顶点坐标是（）

A、 $(3 ， 4)$ B、 $(- 3 ， 4)$ C、 $(3 ， - 4)$ D、 $(2 ， 4)$

查看试题解析
7. 如图，二次函数 $y = a (x + 1)^{2} + k$ 的图象与 $x$ 轴交于 $A (- 3 ， 0)$ ， B两点，下列说法错误的是（）

A、 $a < 0$ B、图象的对称轴为直线 $x = - 1$ C、点B的坐标为 $(1 ， 0)$ D、当 $x < 0$ 时，y随x的增大而增大

查看试题解析
8. 将二次函数 $y = 2 x^{2}$ 的图象向右平移2个单位，再向下平移3个单位，得到的函数图象的表达式是（　　）

A、 $y = 2 {(x + 2)}^{2} + 3$ B、 $y = 2 {(x + 2)}^{2} -3$ C、 $y = 2 {(x -2)}^{2} -3$ D、 $y = 2 {(x -2)}^{2} + 3$

查看试题解析
9. 秋冬季节为流感得高发期，有一人患了流感，经过两轮传染后共有81人患了流感，每轮传染中平均一个人传染的人数为（）

A、7人 B、8人 C、9人 D、10人

查看试题解析
10. 小匡同学从市场上买一块长80cm、宽70cm的矩形铁皮，准备制作一个工具箱．如图，他将矩形铁皮的四个角各剪掉一个边长xcm的正方形后，剩余的部分刚好能围成一个底面积为3000 $c m^{2}$ 的无盖长方形工具箱，根据题意列方程为（）

A、 $(80 - x) (70 - x) = 3000$ B、 $80 \times 70 - 4 x^{2} = 3000$ C、 $(80 - 2 x) (70 - 2 x) = 3000$ D、 $80 \times 70 - 4 x^{2} - (70 + 80) x = 3000$

查看试题解析
11. 如图是二次函数 $y = a x^{2} + b x + c$ 的部分图象，由图象可知不等式 $a x^{2} + b x + c < 0$ 的解集是（）

A、 $- 1 < x < 5$ B、 $x > 5$ C、 $x < - 1$ 且 $x > 5$ D、x＜－1或x＞5

查看试题解析
12. 如图，抛物线y＝ax²+bx+c（a≠0）与x轴交于点A（-1，0）和B，与y轴交于点C给出下列结论：①abc＞0；②2a+b＜0；③4a-2b+c＞0；⑨④3a+c＞0．其中正确的结论个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

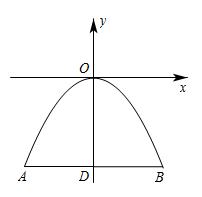
13. 一元二次方程x²+3x=0的解是．

查看试题解析
14. 若x= $- 1$ 是一元二次方程 $x^{2} + 2 x + n = 0$ 的一个根，则n的值为 .

查看试题解析
15. 抛物线 $y = - x^{2} + 3 x - \frac{5}{2}$ 的对称轴是直线．

查看试题解析
16. 赵州桥的桥拱横截面是近似的抛物线形，其示意图如图所示，其解析式为y＝- $\frac{1}{25}$ x² ．当水面离桥拱顶的高度DO为4m时，水面宽度AB为m．

查看试题解析
17. 一个两位数，个位数字比十位数字少1，且个位数字与十位数字的乘积等于72，则这个两位数是．

查看试题解析
18. 设抛物线 $y = x^{2} + (a + 1) x + a$ ，其中a为实数．

(1)、若抛物线经过点 $(- 1 ， m)$ ，则 $m =$ ；

(2)、将抛物线 $y = x^{2} + (a + 1) x + a$ 向上平移2个单位，所得抛物线顶点的纵坐标的最大值是．

查看试题解析

三、解答题

19. 解下列方程

(1)、x2-6x-16=0（配方法）；

(2)、 $2 x^{2} - 2 \sqrt{2} x + 1 = 0$ （公式法）．

查看试题解析
20. 解下列方程

(1)、 $3 x (x - 1) = 2 (x - 1)$

(2)、 $(2 x - 1)^{2} = (3 - x)^{2}$ ．

查看试题解析
21. 已知二次函数 $y = x^{2} - 4 x + 3$ ．

(1)、求出该二次函数图象的顶点坐标．

(2)、填写下列表格：
x
…
0
1
2
3
4
…
y
…
3
0
…

(3)、在图中所示的坐标系中画出该二次函数的图象．

查看试题解析
22. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象上部分点的横坐标x与纵坐标y的对应值如下表所示：
x
…
－1
0
2
4
…
y
…
－5
1
1
m
…
求：

(1)、这个二次函数的解析式；

(2)、这个二次函数图象的顶点坐标及上表中m的值．

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 12 c m$ ， $B C = 24 c m$ ，动点 $P$ 从点 $A$ 开始沿边 $A B$ 向点 $B$ 以 $2 c m / s$ 的速度移动，动点 $Q$ 从点 $B$ 开始沿边 $B C$ 向点 $C$ 以 $4 c m / s$ 的速度移动，如果 $P$ ， $Q$ 两点分别从 $A$ ， $B$ 两点同时出发，设运动时间为 $x$ $s$ ．

(1)、用含x的式子表示：
$A P =$ $c m$ ，

$B P =$ $c m$ ，

$B Q =$ $c m$ ，

(2)、当 $△ P B Q$ 的面积为 $32 c m^{2}$ 时，求运动时间；

(3)、四边形 $A P Q C$ 的面积能否等于 $172 c m^{2}$ ？若能，求出运动的时间；若不能，说明理由．

查看试题解析
24. 某水果商店销售一种进价为40元/千克的优质水果，若售价为50元/千克，则一个月可售出500千克；若售价在50元/千克的基础上每涨价1元，则月销售量就减少10千克．

(1)、当售价为55元/千克时，每月销售水果多少千克？

(2)、当每千克水果售价为多少元时，获得的月利润最大？

查看试题解析
25. 已知抛物线 $y = \frac{1}{4} x^{2} + 1$ 具有如下性质：给抛物线上任意一点到定点 $F (0 ， 2)$ 的距离与到x轴的距离相等，如图，点M的坐标为 $(\sqrt{3} ， 3)$ ， P是抛物线 $y = \frac{1}{4} x^{2} + 1$ 上一动点，则

(1)、当 $△ P O F$ 面积为4时，求P点的坐标；

(2)、求 $△ P M F$ 周长的最小值．

查看试题解析
26. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 4 (a \neq 0)$ 与x轴交于点 $A (- 1 ， 0)$ ， $B (4 ， 0)$ ，与y轴交于点C．

(1)、求该抛物线的解析式及对称轴；

(2)、直线l为该抛物线的对称轴，点D与点C关于直线l对称，点P为直线AD下方抛物线上一动点，连接PA，PD，求△PAD面积的最大值．

查看试题解析

x	…	0	1	2	3	4	…
y	…	3	0				…

x	…	－1	0	2	4	…
y	…	－5	1	1	m	…