天津市河西区2022-2023学年九年级上学期期中考试数学试卷
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 在抛物线上的点为( )A、(1,0) B、(2,2) C、(-1,1) D、(0,1)2. 在艺术字中,有些字母是中心对称图形,下面的5个字母中,是中心对称图形的有( )
 A、2个 B、3个 C、4个 D、5个3. 解方程的结果为( )A、 B、 C、 , D、 ,4. 正方体的六个面是全等的正方形,设正方体的棱长为x,表面积为y,则y是x的函数,它们的关系式为( )A、 B、 C、 D、5. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )
A、2个 B、3个 C、4个 D、5个3. 解方程的结果为( )A、 B、 C、 , D、 ,4. 正方体的六个面是全等的正方形,设正方体的棱长为x,表面积为y,则y是x的函数,它们的关系式为( )A、 B、 C、 D、5. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )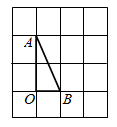 A、
A、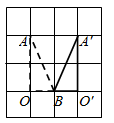 B、
B、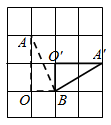 C、
C、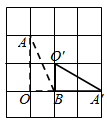 D、
D、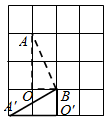 6. 下列二次函数的图象中,开口最小的是( )A、 B、 C、 D、7. 已知二次函数 , 当自变量时,函数值为( )A、 B、 C、 D、8. 若关于x的一元二次方程有两个相等的实数根,则a的取值为( )A、 B、 C、 D、9. 要组织一次排球邀请赛,参赛的每两个各队之间都要比赛一场,根据场地和时间等条件,赛程计划安排共计28场比赛,比赛组织者应邀请多少个队参赛?若设应邀请x个队参赛,可列出的方程为( )A、 B、 C、 D、10. 将抛物线向右平移1个单位,新的函数解析式为( )A、 B、 C、 D、11. 如图,在中, , 将绕点C顺时针旋转得到 , 使点B的对应点E恰好落在边上,点A的对应点为D,延长交于点F,则下列结论一定正确的是( )
6. 下列二次函数的图象中,开口最小的是( )A、 B、 C、 D、7. 已知二次函数 , 当自变量时,函数值为( )A、 B、 C、 D、8. 若关于x的一元二次方程有两个相等的实数根,则a的取值为( )A、 B、 C、 D、9. 要组织一次排球邀请赛,参赛的每两个各队之间都要比赛一场,根据场地和时间等条件,赛程计划安排共计28场比赛,比赛组织者应邀请多少个队参赛?若设应邀请x个队参赛,可列出的方程为( )A、 B、 C、 D、10. 将抛物线向右平移1个单位,新的函数解析式为( )A、 B、 C、 D、11. 如图,在中, , 将绕点C顺时针旋转得到 , 使点B的对应点E恰好落在边上,点A的对应点为D,延长交于点F,则下列结论一定正确的是( ) A、 B、 C、 D、12. 已知抛物线( , , 是常数, , )经过点 , 其对称轴是直线 . 有下列结论:
A、 B、 C、 D、12. 已知抛物线( , , 是常数, , )经过点 , 其对称轴是直线 . 有下列结论:① ;② 关于的方程有两个不等的实数根;③ .
其中,正确结论的个数是( )
A、3 B、2 C、1 D、0二、填空题
-
13. 点关于原点对称点的坐标为 .14. 时钟上的时针匀速旋转一周是12小时,从5时到6时,时针转动的度数为 .15. 若关于x的一元二次方程 有两个不相等的实数根,则m的值可以是.(写出一个即可)16. 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把绕点B逆时针旋转90°,得 , 点A、O旋转后的对应点为 , , 那么A的长为 .
 17. 如图,将△ABC绕着点C顺时针旋转50°后得到△A’B’C.若=40°,=110°,则∠的度数为.
17. 如图,将△ABC绕着点C顺时针旋转50°后得到△A’B’C.若=40°,=110°,则∠的度数为. 18. 如图是一个三角点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点……,它们的前n行点数和为 .
18. 如图是一个三角点阵,从上向下有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点……,它们的前n行点数和为 .
三、解答题
-
19. 解方程(1)、 ;(2)、20. 如图,若将线段绕点O旋转 , 得到点A的对应点 , 点B的对应点为 .
 (1)、画出旋转后的图形,并连接;(2)、四边形的形状一定为 . (填写序号即可)
(1)、画出旋转后的图形,并连接;(2)、四边形的形状一定为 . (填写序号即可)①矩形;②菱形;③平行四边形;④不能确定形状的任意四边形
21. 已知抛物线 . (1)、画出这条抛物线的草图;(2)、抛物线有最点(填“高”或“低”),该点是;(3)、利用图象直接回答:当x取什么值时,函数值大于0?22. 如图,已知在中, , 将绕点B顺时针旋转得到 , 和交于点 P,连接 , .
(1)、画出这条抛物线的草图;(2)、抛物线有最点(填“高”或“低”),该点是;(3)、利用图象直接回答:当x取什么值时,函数值大于0?22. 如图,已知在中, , 将绕点B顺时针旋转得到 , 和交于点 P,连接 , . (1)、和都是等边三角形吗?说明理由;(2)、求的度数.23. 如图,利用一面墙(墙长20米),用总长度43米的篱笆(图中实线部分)围成一个矩形鸡舍 , 且中间共留两个1米的小门,设篱笆长为x米.
(1)、和都是等边三角形吗?说明理由;(2)、求的度数.23. 如图,利用一面墙(墙长20米),用总长度43米的篱笆(图中实线部分)围成一个矩形鸡舍 , 且中间共留两个1米的小门,设篱笆长为x米. (1)、米(用含x的代数式表示);(2)、若矩形鸡舍面积为150平方米,求篱笆的长?(3)、矩形鸡舍面积的最大值是多少?说明理由.24. 在平面直角坐标系中,已知为坐标原点,点 , . 以点为旋转中心,把顺时针旋转,得 .
(1)、米(用含x的代数式表示);(2)、若矩形鸡舍面积为150平方米,求篱笆的长?(3)、矩形鸡舍面积的最大值是多少?说明理由.24. 在平面直角坐标系中,已知为坐标原点,点 , . 以点为旋转中心,把顺时针旋转,得 . (1)、如图①,当旋转后满足轴时,求点C的坐标;(2)、如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标;(3)、在(2)的条件下,边OB上的一点旋转后的对应点为当取得最小值时,求点的坐标(直接写出结果即可).25. 已知抛物线过点 , 且与轴交于点 .(1)、求该抛物线的顶点坐标;(2)、若有点A在直线上,过点A作轴于点B,以为斜边,在左侧作等腰直角三角形 .
(1)、如图①,当旋转后满足轴时,求点C的坐标;(2)、如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标;(3)、在(2)的条件下,边OB上的一点旋转后的对应点为当取得最小值时,求点的坐标(直接写出结果即可).25. 已知抛物线过点 , 且与轴交于点 .(1)、求该抛物线的顶点坐标;(2)、若有点A在直线上,过点A作轴于点B,以为斜边,在左侧作等腰直角三角形 .① 当点Q与点A重合时,求点C到抛物线对称轴的距离;
② 若点C恰好落在抛物线上,求此时点C的坐标 .