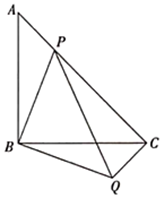
天津市和平区2022-2023学年九年级上学期期中质量调查数学试题
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. “垃圾分类,利国利民”,在2019年7月1日起上海开始正式实施垃圾分类,到2020年底先行先试的46个重点城市,要基本建成垃圾分类处理系统.以下四类垃圾分类标志的图形,其中既是轴对称图形又是中心对称图形的是( )
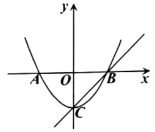
 A、可回收物 B、有害垃圾 C、厨余垃圾 D、其他垃圾2. 一元二次方程 的根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定3. 如图,菱形对角线交点与坐标原点重合,点 , 则点的坐标为( )
A、可回收物 B、有害垃圾 C、厨余垃圾 D、其他垃圾2. 一元二次方程 的根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定3. 如图,菱形对角线交点与坐标原点重合,点 , 则点的坐标为( )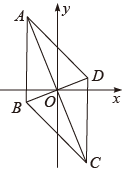 A、 B、 C、 D、4. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、5. AB是⊙O的直径,点C在圆上,∠ABC=65°,那么∠OCA的度数是( )
A、 B、 C、 D、4. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、5. AB是⊙O的直径,点C在圆上,∠ABC=65°,那么∠OCA的度数是( ) A、25° B、35° C、15° D、20°6. 把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )A、y=﹣2(x+1)2+2 B、y=﹣2(x+1)2﹣2 C、y=﹣2(x﹣1)2+2 D、y=﹣2(x﹣1)2﹣27. 若 , , 为二次函数的图象上的三点,则 , , 的大小关系是( )A、 B、 C、 D、8. 某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x)2=182 B、50+50(1+x)+50(1+x)2=182 C、50(1+2x)=182 D、50+50(1+x)+50(1+2x)=1829. 关于二次函数 ,下列说法正确的是( )A、图像与 轴的交点坐标为 B、图像的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-310. 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径
A、25° B、35° C、15° D、20°6. 把抛物线y=﹣2x2先向右平移1个单位长度,再向上平移2个单位长度后,所得函数的表达式为( )A、y=﹣2(x+1)2+2 B、y=﹣2(x+1)2﹣2 C、y=﹣2(x﹣1)2+2 D、y=﹣2(x﹣1)2﹣27. 若 , , 为二次函数的图象上的三点,则 , , 的大小关系是( )A、 B、 C、 D、8. 某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x)2=182 B、50+50(1+x)+50(1+x)2=182 C、50(1+2x)=182 D、50+50(1+x)+50(1+2x)=1829. 关于二次函数 ,下列说法正确的是( )A、图像与 轴的交点坐标为 B、图像的对称轴在 轴的右侧 C、当 时, 的值随 值的增大而减小 D、 的最小值为-310. 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径 A、6米 B、米 C、7米 D、米11. 如图 ,已知△ABC 中,∠C=90°,AC=BC= , 将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
A、6米 B、米 C、7米 D、米11. 如图 ,已知△ABC 中,∠C=90°,AC=BC= , 将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( ) A、2- B、 C、 D、112. 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:
A、2- B、 C、 D、112. 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:x
…
-2
-1
0
1
2
…
y=ax2+bx+c
…
t
m
-2
-2
n
…
且当x=时,与其对应的函数值y>0,有下列结论:
①abc<0;②m=n;③-2和3是关于x的方程ax2+bx+c=t的两个根;④ .
其中,正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
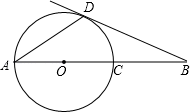
13. 写出下列一元二次方程的根 .14. 抛物线的顶点坐标为 .15. 如图,线段AB经过圆心O,交⊙O于点A、C,∠B=30°,直线BD与⊙O切于点D,则∠ADB的度数是 .
 16. 已知二次函数 的图象与 轴有交点,则 的取值范围是 .17. △ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是.18. 如图,是等边三角形, , D是的中点,F是直线上一动点,线段绕点D逆时针旋转 , 得到线段 , 当点F运动时,的最小值是 .
16. 已知二次函数 的图象与 轴有交点,则 的取值范围是 .17. △ABC为⊙O的内接三角形,若∠AOC=160°,则∠ABC的度数是.18. 如图,是等边三角形, , D是的中点,F是直线上一动点,线段绕点D逆时针旋转 , 得到线段 , 当点F运动时,的最小值是 .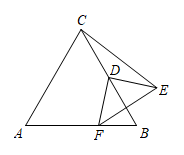
三、解答题
-
19. 解方程:
(Ⅰ)x2+x-12=0;
(Ⅱ)5x(x-1)=2(x-1).
20. 如图,在半径为的中,弦长 . 求: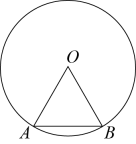 (1)、的度数;(2)、点O到的距离.21. 已知 , 分别与相切于点 , , , 为上一点.
(1)、的度数;(2)、点O到的距离.21. 已知 , 分别与相切于点 , , , 为上一点.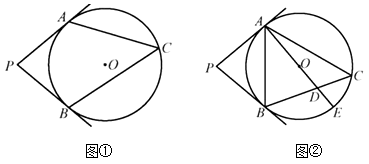
(Ⅰ)如图①,求的大小;
(Ⅱ)如图②,为的直径,与相交于点 , 若 , 求的大小.
22. 如图,某小区规划在一个长30 m,宽20 m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78 m2 , 那么通道的宽应设计成多少m?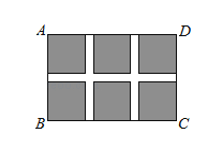 23. 某书店销售复习资料,已知每本复习资料进价为40元,市场调查发现:若以每本50元销售,平均每天可销售90本,在此基础上,若售价每提高1元,则平均每天少销售3本.设涨价后每本的售价为元,书店平均每天销售这种复习资料的利润为元.(1)、涨价后每本复习资料的利润为元,平均每天可销售本;(2)、求与的函数关系式;(3)、当复习资料每本售价为多少时,平均每天的利润最大?最大利润为多少?
23. 某书店销售复习资料,已知每本复习资料进价为40元,市场调查发现:若以每本50元销售,平均每天可销售90本,在此基础上,若售价每提高1元,则平均每天少销售3本.设涨价后每本的售价为元,书店平均每天销售这种复习资料的利润为元.(1)、涨价后每本复习资料的利润为元,平均每天可销售本;(2)、求与的函数关系式;(3)、当复习资料每本售价为多少时,平均每天的利润最大?最大利润为多少?