上海市宝山区2022-2023学年九年级上学期数学期中试题
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 下列各组图形中,一定相似的是( )A、两个矩形 B、两个菱形 C、两个正方形 D、两个等腰梯形2. 在平面直角坐标系中,已知点与原点的连线与轴的正半轴的夹角为 , 那么的值是( )A、3 B、 C、 D、3. 在Rt△ABC中, ,如果∠A= , ,那么线段AC的长可表示为( ).A、 ; B、 ; C、 ; D、 .4. 已知 、 、 都是非零向量,下列条件中,不能判断 的是( )A、 B、 C、 , D、5. 已知的三边长分别为 , , , 的一边长为 , 如果这两个三角形相似,那么的另两边长可能是( )A、 , B、 , C、 , D、 ,6. 如图,在中,点是边的中点,交对角线于点 , 如果 , 那么的面积为( )
 A、6 B、12 C、24 D、36
A、6 B、12 C、24 D、36二、填空题
-
7. 如果 , 那么 的值为8. 已知线段厘米,厘米,那么线段和的比例中项是厘米.9. 已知点P是线段AB的黄金分割点,AB=4厘米,则较短线段AP的长是厘米.10. 已知与相似,且点A与点是对应点,点与点是对应点,如果 , , 那么 .11. 在中,如果 , , , 那么 .12. 已知 , 顶点、、分别与、、对应, , 、分别是边、的中点,如果 , 那么的长为 .13. 在梯形中, , , , 点、分别在边、上,且 , 如果 , 那么的长为 .14. 如图,矩形的边在的边上,顶点、分别在边、上.已知 , , , 那么的面积是 .
 15. △ABC中,AD是中线,G是重心, ,那么 =(用 表示).16. 在中,点、分别在直线、上,如果 , , , , 那么 .17. 如图,图中提供了一种求的方法,作 , 使 , , 再延长到点 , 使 , 联结 , 即可得 , 如果设 , 则可得 , 那么 , 运用以上方法,可求得的值是 .
15. △ABC中,AD是中线,G是重心, ,那么 =(用 表示).16. 在中,点、分别在直线、上,如果 , , , , 那么 .17. 如图,图中提供了一种求的方法,作 , 使 , , 再延长到点 , 使 , 联结 , 即可得 , 如果设 , 则可得 , 那么 , 运用以上方法,可求得的值是 . 18. 如图,矩形中,、分别是边、上的点,将矩形沿直线翻折后,点落在边上的点处,如果 , , , 那么的长为 .
18. 如图,矩形中,、分别是边、上的点,将矩形沿直线翻折后,点落在边上的点处,如果 , , , 那么的长为 .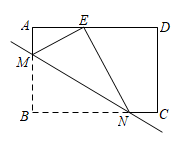
三、解答题
-
19. 计算:20. 如图,已知两个不平行的向量和 , 先化简,再求作:(不要求写作法,但要指出图中表示结论的向量)
 21. 如图,在四边形中,平分 , , .
21. 如图,在四边形中,平分 , , . (1)、求的值;(2)、如果 , 求四边形的面积.22. 如图,在中, , 过点作 , 垂足为点
(1)、求的值;(2)、如果 , 求四边形的面积.22. 如图,在中, , 过点作 , 垂足为点 (1)、求的值﹔(2)、点是延长线上一点,联结 , 当时,求线段的长.23. 已知:如图,在直角梯形中, , , , 为的中点,连结并延长,交线段于点 .
(1)、求的值﹔(2)、点是延长线上一点,联结 , 当时,求线段的长.23. 已知:如图,在直角梯形中, , , , 为的中点,连结并延长,交线段于点 . (1)、求证:;(2)、若 , , 求的长.24. 学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一颗古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米.
(1)、求证:;(2)、若 , , 求的长.24. 学习了相似三角形知识后,小丽同学准备用自制的直角三角形纸板测量校园内一颗古树的高度.已知三角形纸板的斜边长为0.5米,较短的直角边长为0.3米.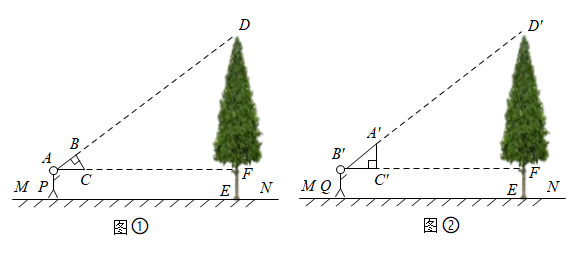 (1)、小丽先调整自己的位置至点 , 将直角三角形纸板的三个顶点位置记为、、(如图①),斜边平行于地面(点、、、在一直线上),且点在边(较长直角边)的延长线上,此时测得边距离地面的高度为1.5米,小丽与古树的距离为16米,求古树的高度;(2)、为了尝试不同的思路,小丽又向前移动自己的位置至点 , 将直角三角形纸板的三个顶点的新位置记为、、(如图②),使直角边(较短直角边)平行于地面(点、、、在一直线上),点在斜边的延长线上,且测得此时边距离地面的高度依然是1.5米,那么小丽向前移动了多少米?25. 如图,正方形中, , 是边上一点(点不与点、重合),点在的延长线上,且 , 联结 , 分别交、于点、 .
(1)、小丽先调整自己的位置至点 , 将直角三角形纸板的三个顶点位置记为、、(如图①),斜边平行于地面(点、、、在一直线上),且点在边(较长直角边)的延长线上,此时测得边距离地面的高度为1.5米,小丽与古树的距离为16米,求古树的高度;(2)、为了尝试不同的思路,小丽又向前移动自己的位置至点 , 将直角三角形纸板的三个顶点的新位置记为、、(如图②),使直角边(较短直角边)平行于地面(点、、、在一直线上),点在斜边的延长线上,且测得此时边距离地面的高度依然是1.5米,那么小丽向前移动了多少米?25. 如图,正方形中, , 是边上一点(点不与点、重合),点在的延长线上,且 , 联结 , 分别交、于点、 .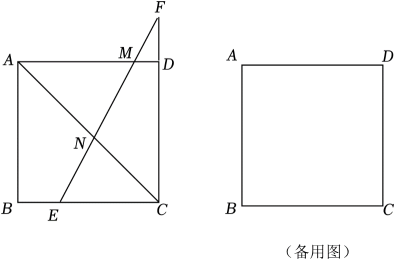 (1)、已知 , 求的长;(2)、求证:;(3)、当是等腰三角形时,求的值.
(1)、已知 , 求的长;(2)、求证:;(3)、当是等腰三角形时,求的值.