山西省朔州市朔城区2022-2023学年九年级上学期期中考试数学试卷
试卷更新日期:2022-12-09 类型:期中考试
一、单选题
-
1. 已知关于x的一元二次方程的一个解是 , 则实数m的值是( )A、1 B、 C、 D、-12. 数学中的对称之美无处不在,下列是小明看到的他所在小区的垃圾桶上的四幅垃圾分类标志图案,如果不考虑图案下面的文字说明,那么这四幅图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,是的直径,为弦, , 在上任取一点D,且点D与点C位于直径的两侧,连接和 , 则的度数是( )
3. 如图,是的直径,为弦, , 在上任取一点D,且点D与点C位于直径的两侧,连接和 , 则的度数是( ) A、 B、 C、 D、4. 下列一元二次方程一定有两个不相等的实数解的方程是( )A、 B、 C、 D、5. 在数学课上,老师给出二次函数的四幅图像如下,根据二次函数的图象的性质可知,下列图像可能表示二次函数( , a,c是常数)的图像是( )A、
A、 B、 C、 D、4. 下列一元二次方程一定有两个不相等的实数解的方程是( )A、 B、 C、 D、5. 在数学课上,老师给出二次函数的四幅图像如下,根据二次函数的图象的性质可知,下列图像可能表示二次函数( , a,c是常数)的图像是( )A、 B、
B、 C、
C、 D、
D、 6. 在应用一元二次方程解决问题时,老师展示出一张图片如图所示,在矩形纸片上截去两个同样大小的圆,要求使两圆的面积和是剩余面积的一半,已知矩形的长和宽分别为和 , 圆的半径为 , 根据题意列方程为( )
6. 在应用一元二次方程解决问题时,老师展示出一张图片如图所示,在矩形纸片上截去两个同样大小的圆,要求使两圆的面积和是剩余面积的一半,已知矩形的长和宽分别为和 , 圆的半径为 , 根据题意列方程为( ) A、 B、 C、 D、7. 如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是 , 请你找出此时的对称中心是( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,画关于点O成中心对称的图形时,由于紧张对称中心选错,画出的图形是 , 请你找出此时的对称中心是( ) A、 B、 C、 D、8. 某钢铁厂七月份产钢50吨,九月份的钢产量比八月份的钢产量增加12吨,若平均每月产钢量的增长率相同且为x,则根据题意,列出的方程正确的是( )A、 B、 C、 D、9. 如图是一个半径为6cm的的纸片,是的内接三角形,分别以直线和折叠纸片,和都经过圆心O,则图中阴影部分的面积是( )
A、 B、 C、 D、8. 某钢铁厂七月份产钢50吨,九月份的钢产量比八月份的钢产量增加12吨,若平均每月产钢量的增长率相同且为x,则根据题意,列出的方程正确的是( )A、 B、 C、 D、9. 如图是一个半径为6cm的的纸片,是的内接三角形,分别以直线和折叠纸片,和都经过圆心O,则图中阴影部分的面积是( ) A、 B、 C、 D、10. 在平面直角坐标系中,抛物线 与 轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为( )A、 B、 C、 D、
A、 B、 C、 D、10. 在平面直角坐标系中,抛物线 与 轴交于点 ,则该抛物线关于点 成中心对称的抛物线的表达式为( )A、 B、 C、 D、二、填空题
-
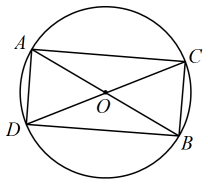
11. 在平面直角坐标系中,点 , 连接OA,把线段OA绕原点O逆时针旋转90°得到线段 , 则点的坐标是 .12. 如图,和是的两条直径,顺次连接 , , 和 , 得到四边形 , 则四边形的形状一定是 .
 13. 已知矩形的面积是 , 当把这个矩形的长减少1cm,宽增加2cm后,所得四边形是正方形,若矩形的宽为xcm,则根据题意,列方程为 .14. 如图,点 , 点 , 线段绕点A逆时针旋转得到线段 , 连接 , 再把绕点A逆时针旋转得到 , 点C的对应点为点 , 则点的坐标是 .
13. 已知矩形的面积是 , 当把这个矩形的长减少1cm,宽增加2cm后,所得四边形是正方形,若矩形的宽为xcm,则根据题意,列方程为 .14. 如图,点 , 点 , 线段绕点A逆时针旋转得到线段 , 连接 , 再把绕点A逆时针旋转得到 , 点C的对应点为点 , 则点的坐标是 . 15. 如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF= .
15. 如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF= .
三、解答题
-
16.(1)、解方程:;(2)、求二次函数的图象与x轴的交点坐标.17. 已知方程是关于x的一元二次方程.(1)、当时,求该方程的根;(2)、若该方程有两个不相等的实数根,求m的取值范围.18. 如图,在平面直角坐标系中,A,B,C三点的坐标依次为 , , . 根据题意,解答下列问题.
 (1)、画出关于原点O成中心对称的;(2)、把绕点顺时针旋转90°得到;(3)、连接 , 和 , 直接写出的面积.19. 如图1,灌溉车沿着平行于绿化带底部边线的方向行驶,为绿化带浇水,喷水口H离地竖直高度为 . 如图2,把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象,把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度为 . 下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为 , 高出喷水口 , 喷出的水最远落在地面C处.
(1)、画出关于原点O成中心对称的;(2)、把绕点顺时针旋转90°得到;(3)、连接 , 和 , 直接写出的面积.19. 如图1,灌溉车沿着平行于绿化带底部边线的方向行驶,为绿化带浇水,喷水口H离地竖直高度为 . 如图2,把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象,把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度为 . 下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为 , 高出喷水口 , 喷出的水最远落在地面C处.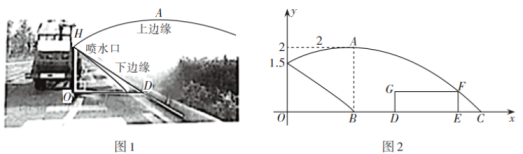 (1)、求上边缘抛物线的函数解析式(用顶点式表示),并求喷出水的最大射程;(2)、灌溉车行驶时喷出的水能浇灌到整个绿化带,喷出的水恰好经过点F时,求此时点F的坐标.20. 如图,在中, , , 对角线 , 点E在射线的延长线上,连接 , 在上取点O,以点O为圆心,长为半径作与射线切于点B,交于点F,交于点M.
(1)、求上边缘抛物线的函数解析式(用顶点式表示),并求喷出水的最大射程;(2)、灌溉车行驶时喷出的水能浇灌到整个绿化带,喷出的水恰好经过点F时,求此时点F的坐标.20. 如图,在中, , , 对角线 , 点E在射线的延长线上,连接 , 在上取点O,以点O为圆心,长为半径作与射线切于点B,交于点F,交于点M. (1)、求证:;(2)、求的长;(3)、连接 , , 直接写出四边形的形状和面积.21. 开发商在新建的某小区划出一个长为90米,宽为60米的矩形场地,计划在其中修建四个面积相等的休闲区,并将余下的空地修建成横向宽为米,纵向宽为米的鹅卵石健身道如图所示.已知修建平方米的休闲区需要费用100元,修建平方米的鹅卵石健身道需要费用200元,开发商投入的资金是元.
(1)、求证:;(2)、求的长;(3)、连接 , , 直接写出四边形的形状和面积.21. 开发商在新建的某小区划出一个长为90米,宽为60米的矩形场地,计划在其中修建四个面积相等的休闲区,并将余下的空地修建成横向宽为米,纵向宽为米的鹅卵石健身道如图所示.已知修建平方米的休闲区需要费用100元,修建平方米的鹅卵石健身道需要费用200元,开发商投入的资金是元. (1)、求与的函数关系式,并直接写出的取值范围;(2)、若开发商预计投入的资金为658800元,求的值.22. 综合与探究
(1)、求与的函数关系式,并直接写出的取值范围;(2)、若开发商预计投入的资金为658800元,求的值.22. 综合与探究问题呈现:
“智慧”数学小组在课外数学活动中研究了一个问题,请帮他们解决,如图1,在正方形的边上任取一点E,以为边在与正方形的同侧作正方形 .
(1)、探究结论:
连接 , 则与的数量关系是 , 位置关系是.
(2)、探究发现:如图2,在图1的基础上连接 , , 作的中点M,连接 , 判断与的数量关系和位置关系,并证明你的结论;
(3)、探究拓展:“智慧”数学小组把“边上任取一点E”改成了“边的延长线上任取一点E”,其余条件不变,请在图3中补全图形,并直接写出(2)中的结论是否符合题意,若不符合题意,请直接写出正确的结论.
23. 综合与实践如图,抛物线与x轴交于A,B两点,且点A在点B的左侧,与y轴交于点C,点D是抛物线上的一动点.
 (1)、求A,B,C三点的坐标;(2)、如图2,当点D在第四象限时,连接和 , 得到 , 当的面积最大时,求点D的坐标;(3)、点E在x轴上运动,以点B,C,D,E为顶点的四边形是平行四边形,请借助图1探究,直接写出点E的坐标.
(1)、求A,B,C三点的坐标;(2)、如图2,当点D在第四象限时,连接和 , 得到 , 当的面积最大时,求点D的坐标;(3)、点E在x轴上运动,以点B,C,D,E为顶点的四边形是平行四边形,请借助图1探究,直接写出点E的坐标.