山西省吕梁市交城县2022-2023学年九年级上学期期中考试数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、等边三角形 B、正五角星 C、正六边形 D、平行四边形

查看试题解析
2. 一元二次方程 $x^{2} - 2 x - 3 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
3. 我们学习了一次函数、二次函数和反比例函数，回顾学习过程，都是按照列表、描点、连线得到函数的图象，然后根据函数的图象研究函数的性质，这种研究方法主要体现的数学思想是（）

A、演绎 B、数形结合 C、抽象 D、公理化

查看试题解析
4. 如图所示，将一个含30°角的直角三角板ABC绕点A旋转，使得点B，A，C′在同一直线上，则三角板ABC旋转的度数是（）．

A、60° B、90° C、120° D、150°

查看试题解析

5. 二次函数

y = a x^{2} + b x + c

（a≠0）中x，y的部分对应值如下表：

x	…	-2	-1	0	1	2	…
y	…	0	-4	-6	-6	-4	…

则该二次函数图象的对称轴为（）

A、y轴 B、直线x＝

\frac{1}{2}

C、直线x＝1 D、直线x＝

\frac{3}{2}

查看试题解析

6. 将抛物线 $y = - 2 x^{2} - 1$ 向左平移1个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为（）

A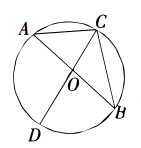、 $y = - 2 (x - 1)^{2} - 2$ B、 $y = - 2 {(x + 1)}^{2} - 2$ C、 $y = - 2 (x - 1)^{2} + 4$ D、 $y = - 2 (x + 1)^{2} - 4$

查看试题解析
7. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆， $C D$ 是 $⊙ O$ 的直径， $∠ B = 35 °$ ，则 $∠ A C D$ 的度数是（）

A、 $45 °$ B、 $50 °$ C、 $55 °$ D、 $60 °$

查看试题解析
8. 有一个两位数，个位数字与十位数字之和为8，把它的个位数字与十位数字对调，得到一个新数，新数与原数之积为1855，则原两位数是（）

A、35 B、53 C、62 D、35或53

查看试题解析
9. 已知二次函数 $y = 2 x^{2} - 8 x + c$ 的图象过点A $(- 2 ， y_{1})$ ， B $(- 1 ， y_{2})$ ， $C (8 ， y_{3})$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{3} < y_{2}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的图象与 $x$ 轴交于点A，B，且点A在 $- 1$ 和0之间，图象与 $y$ 轴交于负半轴，对称轴为直线 $x = 1$ ，对于该二次函数，下列结论中错误的是（）

A、二次函数的最小值为 $a + b + c$ B、 $b^{2} - 4 a c > 0$ C、 $a - b + c < 0$ D、 $9 a + 3 b + c > 0$

查看试题解析

二、填空题

11. 抛物线 $y = {(x - 2)}^{2} + 1$ 的顶点坐标是.

查看试题解析
12. 在2020年太原五中秋季运动会上，某班参加圆周接力的同学每两人握一次手，共握手190次，设参加圆周接力的人数为x，则可列方程为.

查看试题解析
13. 飞机着陆后滑行的距离s（单位：m）关于滑行的时间t（单位：s）的函数解析式是 $s = - \frac{3}{2} t^{2} + 60 t$ ．则飞机着陆后滑行的最大距离是m．

查看试题解析
14. 已知关于 $x$ 的方程 $a {(x + c)}^{2} = b$ （ $a ， b ， c$ 为常数， $a \neq 0$ ）的两根分别为 $- 3$ ， $1$ ，那么关于 $y$ 的方程 $a (y + c - 3)^{2} = b$ 的两根分别为．

查看试题解析
15. 如图， $△ A B C$ 绕点 $A$ 逆时针旋转 $45 °$ 得到 $△ A B^{'} C^{'}$ ，若 $∠ B A C = 90 °$ ， $A B = A C = \sqrt{2}$ ，则图中阴影部分的面积等于．

查看试题解析

三、解答题

16. 解下列方程：

(1)、 $2 (x + 3)^{2} = 8$ ；

(2)、 $x^{2} + 2 x - 17 = 0$ ．

查看试题解析
17. 已知关于x的一元二次方程 $x^{2} + (2 k - 1) x + k^{2} - 1 = 0$ 的两个实数根分别为 $x_{1}$ ， $x_{2}$ ．

(1)、求k的取值范围；

(2)、若 $x_{1}$ ， $x_{2}$ 满足 $x_{1}^{2} + x_{2}^{2} = 16 + x_{1} x_{2}$ ，求实数k的值．

查看试题解析
18. 正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：
⑴作出△ABC绕点A逆时针旋转90°的△AB₁C₁ ．
⑵作出△AB₁C₁关于原点O成中心对称的△A₁B₂C₂ ．
⑶请直接写出以A₁、B₂、C₂为顶点的平行四边形的第四个顶点D的坐标．

查看试题解析
19. 如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD＝CD，过点D作⊙O的切线交边AC于点F.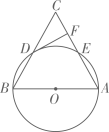

(1)、求证：DF⊥AC；

(2)、若⊙O的半径为5，∠CDF＝30°，求弧BD的长(结果保留π)．

查看试题解析
20. 阅读以下材料，并按要求完成相应的任务．
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题：今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？用现在的数学语言表达是：如图， $C D$ 为 $⊙ O$ 的直径，弦 $A B ⊥ C D$ ，垂足为 $E$ ， $C E = 1$ 寸， $A B = 1$ 尺，其中1尺 $= 10$ 寸，求出直径 $C D$ 的长．
解题过程如下：
连接 $O A$ ，设 $O A = r$ 寸，则 $O E = r - C E = (r - 1)$ 寸．
∵ $A B ⊥ C D ， A B = 1$ 尺，∴ $A E = \frac{1}{2} A B = 5$ 寸．
在 $R t △ O A E$ 中， $O A^{2} = A E^{2} + O E^{2}$ ，即 $r^{2} = 5^{2} + {(r - 1)}^{2}$ ，解得 $r = 13$ ，
∴ $C D = 2 r = 26$ 寸．
任务：

(1)、上述解题过程运用了定理和定理．

(2)、若原题改为已知 $D E = 25$ 寸， $A B = 1$ 尺，请根据上述解题思路，求直径 $C D$ 的长．

(3)、若继续往下锯，当锯到 $A E = O E$ 时，弦 $A B$ 所对圆周角的度数为．

查看试题解析
21. 某商店经销一种学生用双肩包，已知这种双肩包的成本价为每个30元.市场调查发现，这种双肩包每天的销售量y（个）与销售单价x（元）有如下关系：y=﹣x+60（30≤x≤60）.设这种双肩包每天的销售利润为w元.

(1)、求w与x之间的函数关系式；

(2)、这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？

(3)、如果物价部门规定这种双肩包的销售单价不高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少.

查看试题解析
22. 综合与实践
【情境呈现】如图1，将两个正方形纸片 $A B C D$ 和 $A E F G$ 放置在一起.若固定正方形 $A B C D$ ，将正方形 $A E F G$ 绕着点A旋转．

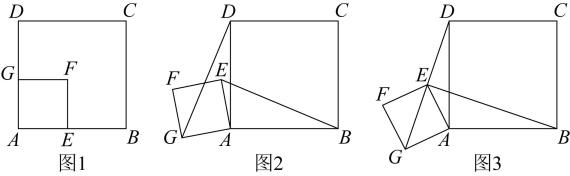(1)、【数学思考】如图1，当点E在 $A B$ 边上，点G在 $A D$ 边上时，线段 $B E$ 与 $D G$ 的数量关系是，位置关系是．

(2)、如图2，是将正方形 $A E F G$ 绕着点A逆时针旋转 $α$ 度得到的，则（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

(3)、【拓展探究】如图3，若点D，E，G在同一条直线上，且 $A B = 2 A E = 2 \sqrt{2}$ ，求线段 $B E$ 的长度（直接写出答案）．

查看试题解析
23. 如图，已知抛物线 $y = a x^{2} + b x + c$ $（ a \neq 0 ）$ 的顶点坐标为Q $(2 ， - 1)$ ，且与 $y$ 轴交C $(0 ， 3)$ ，与 $x$ 轴交于A，B两点（点A在点B的右侧），点P是抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作 $P D ⊥$ 直线 $A C$ 于点D．

(1)、求该抛物线的解析式及A，B两点的坐标；

(2)、求点P在运动的过程中，线段PD的最大值；

(3)、若点P与点Q重合，点E在 $x$ 轴上，点F在抛物线上，问是否存在以A，P，E，F为顶点的平行四边形？若存在，直接写出点F的坐标；若不存在，请说明理由．

查看试题解析