青海省海东市2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中是关于x的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x} = 0$ B、ax²+bx+c＝0 C、(x﹣1)(x﹣2)＝0 D、3x²+2＝x²+2(x﹣1)²

查看试题解析
2. 下列函数中，是二次函数的是（）

A、 $y = - 8 x$ B、 $y = \frac{8}{x}$ C、 $y = 8 x^{2}$ D、 $y = 8 x - 4$

查看试题解析
3. 一元二次方程 $x^{2} - 2 x + 1 = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
4. 若两个连续奇数的积为63，则这两个数的和为（）

A、16 B、17 C、±16 D、±17

查看试题解析
5. 抛物线 $y = {(x - 1)}^{2} - 3$ 的对称轴是（）

A、y轴 B、直线 $x = - 1$ C、直线 $x = 1$ D、直线 $x = - 3$

查看试题解析
6. 二次函数 $y = {(x - \frac{3}{2})}^{2} + \frac{3}{4}$ 的图象 $(1 \leq x \leq 3)$ 如图所示，则该函数在所给自变量的取值范围内，函数值y的取值范围是（）

A、 $y \geq 1$ B、 $1 \leq y \leq 3$ C、 $\frac{3}{4} \leq y \leq 3$ D、 $0 \leq y \leq 3$

查看试题解析
7. 将方程3x（x-1）=5（x+2）化成一元二次方程的一般形式后，一次项系数是（）

A、3 B、-8x C、-8 D、-10

查看试题解析
8. 抛物线 $y = 3 x^{2}$ 向右平移1个单位，再向下平移2个单位，所得到的抛物线是（）

A、 $y = 3 {(x - 1)}^{2} - 2$ B、 $y = 3 {(x + 1)}^{2} - 2$ C、 $y = 3 {(x + 1)}^{2} + 2$ D、 $y = 3 {(x - 1)}^{2} + 2$

查看试题解析
9. 若 $x_{1}$ 、 $x_{2}$ 是一元二次方程 $x^{2} + 3 x - 5 = 0$ 的两根，则 $x_{1} \cdot x_{2}$ 的值是（）

A、3 B、-3 C、5 D、-5

查看试题解析
10. 一元二次方程x²－8x－1=0配方后为（）

A、(x－4)²=17 B、(x＋4)²=15 C、(x＋4)²=17 D、(x－4)²=17或(x＋4)²=17

查看试题解析

二、填空题

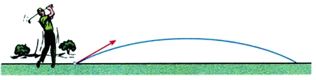
11. 若方程 $(m - 2) x^{m^{2} - 2} + 3 x = 0$ 是关于x的一元二次方程，则m的值为．

查看试题解析
12. 如图，若被击打的小球飞行高度 $h$ （单位： $m$ ）与飞行时间 $t$ （单位： $s$ ）之间具有的关系为 $h = 20 t - 5 t^{2}$ ，则小球从飞出到落地所用的时间为 $s$ ．

查看试题解析
13. 在二次函数y=-x²+1中，二次项系数、一次项系数、常数项的和为．

查看试题解析
14. 方程2x²+1=3x的解为．

查看试题解析
15. 二次函数y＝2x²+bx+3的图象的对称轴是直线x＝1，则常数b的值为．

查看试题解析
16. 二次函数 $y = - x^{2} - x - 1$ 的图像有最点．（填“高”或“低”）

查看试题解析
17. 已知四个二次函数的图象如图所示，那么a₁ ， a₂ ， a₃ ， a₄的大小关系是．（请用“＞”连接排序）

查看试题解析
18. 若函数 $y = (m - 2) x^{| m |} + 1$ （m是常数）是二次函数，则m的值是.

查看试题解析
19. 把函数 $y = 2 x^{2} - 4 x - 1$ 写成 $y = a {(x - h)}^{2} + k$ 的形式，则 $h + k =$ ．

查看试题解析
20. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - 2 x + 1 = 0$ 的两个根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}} =$ ．

查看试题解析

三、解答题

21. 若二次函数 $y = a x^{2} + b x + c$ 的x与y的部分对应值如下表：
x
-2
01
0
1
e
y
d
3
5
3
-27

(1)、求二次函数的表达式；

(2)、求d，e的值．

查看试题解析
22. 解方程：

(1)、 $x^{2} - 3 x + 1 = 0$ ；

(2)、 $3 x (x - 2) = 2 (2 - x)$ ；

(3)、 $x^{2} + 4 x - 5 = 0$ ．

查看试题解析
23. 已知二次函数 $y = - x^{2} + 2 x - m$ （ $m$ 是常数）．

(1)、若该函数的图象与 $x$ 轴有两个不同的交点，求 $m$ 的取值范围．

(2)、若该二次函数的图象与 $x$ 轴的其中一个交点坐标为 $(- 1 ， 0)$ ，求一元二次方程 $- x^{2} + 2 x - m = 0$ 的解．

查看试题解析
24. 如图是某公园一喷水池(示意图)，在水池中央有一垂直于地面的喷水柱，喷水时，水流在各方向沿形状相同的抛物线落下．若水流喷出的高度y(m)与水平距离x(m)之间的函数关系式为y＝－(x－1)²＋2.25．

(1)、求喷出的水流离地面的最大高度；

(2)、求喷嘴离地面的高度；

(3)、若把喷水池改成圆形，则水池半径至少为多少时，才能使喷出的水流不落在水池外？

查看试题解析
25. 某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙（墙足够长），已知计划中的建筑材料可建围墙的总长度为50m ．设饲养室为长为x（m），占地面积为 $y (m^{2})$ ．

(1)、如图1，问饲养室为长x为多少时，占地面积y 最大？

(2)、如图2，现要求在图中所示位置留2m的门，且仍使饲养室占地面积最大．小敏说：“只要饲养室长比（1）中的长多2m就行了．”请你通过计算，判断小敏的说法是否符合题意．

查看试题解析
26. 如图，一块长和宽分别为60厘米和40厘米的长方形铁皮，要在它的四角截去四个相等的小正方形，折成一个无盖的长方体水槽，使它的底面积为800平方厘米．求截去正方形的边长．

查看试题解析
27. 关于x的一元二次方程2（x-1）²+b（x-1）+c＝0化为一般形式后为2x²-3x-1＝0，试求b，c的值．

查看试题解析

x	-2	01	0	1	e
y	d	3	5	3	-27