江西省九江市湖口县2022-2023学年九年级上学期期中数学试卷

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列命题中，真命题是（）．

A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形

查看试题解析
2. 直线 $y = x + a$ 不经过第二象限，则关于x的一元二次方程 $a x^{2} + 2 x + 1 = 0$ 的解的情况是（）

A、无法确定 B、无实数根 C、两个相等的实根 D、两个不相等的实根

查看试题解析
3. 如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于H，则DH等于（）

A、 $\frac{24}{5}$ B、 $\frac{12}{5}$ C、5 D、4

查看试题解析
4. 一元二次方程 $x^{2} - m x - 2 = 0$ 的一个根为2，则m的值是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 如图，一个小球在在地板上自由滚动，并随机停在某块方砖上，如果每一块方砖除颜色外完全相同，那么小球最终停留在黑砖上的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
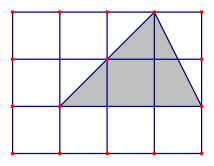6. 如图，已知在等腰Rt△ABC中，∠ACB＝90°，AD为BC边的中线，过点C作CE⊥AD于点E，交AB于点F．若AC＝2，则线段EF的长为（）

A、 $\frac{3}{5}$ B、 $\frac{4 \sqrt{5}}{15}$ C、 $\frac{2 \sqrt{5}}{15}$ D、 $\frac{2}{3}$

查看试题解析

二、填空题

7. 已知三角形两边的长分别是2和3，第三边的长是方程 $x^{2} - 8 x + 12 = 0$ 的根，则这个三角形的周长为．

查看试题解析
8. 同时掷两枚形状、大小、质地完全相同的骰子，至少有一枚骰子的点数是3的概率为．

查看试题解析
9. 如图，四边形ABCD是周长为20的菱形，点A的坐标是（0，4），则点B的坐标为．

查看试题解析
10. 若 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} - 3 x - 1 = 0$ 的两个实数根，则 ${x_{1}}^{2} - x_{1} + 2 x_{2}$ 的值为．

查看试题解析
11. 如图，点D、E分别在AB、AC上，且∠ABC＝∠AED．若DE＝4，AE＝5，BC＝8，则AB的长为

查看试题解析
12. 无论 $x$ 取何整数， $\sqrt{x^{2} - (m - 3) x + m}$ 的值都是整数，则 $m$ 的值为．

查看试题解析

三、解答题

13. 用适当的方法解下列方程：

(1)、x²+2x＝3；

(2)、（x+3）（2-x）＝5．

查看试题解析
14. 一农场要建一个长方形的养鸡场，养鸡场的一边靠墙（墙长15m），另三边用木栏围成，木栏的长为30m，若养鸡场的面积能达到 $100 m^{2}$ ，则养鸡场的长和宽各为多少？

查看试题解析
15. 如图，在矩形ABCD中，点E、F分别在边AD、DC上，BE⊥EF，AB＝6，AE＝9，DE＝2，求EF的长．

查看试题解析
16. 关于x的一元二次方程 $x^{2} - m x + 2 m - 4 = 0$

(1)、求证：方程总有两个实数根．

(2)、若方程的一个根为1，求方程的另一个根．

查看试题解析
17. 在平行四边形 $A B C D$ 中，E为 $A D$ 的中点，请仅用无刻度的直尺完成下列画图，不写画法，保留画图痕迹．

(1)、如图1，在 $B C$ 上找出一点M，使点M是 $B C$ 的中点；

(2)、如图2，在 $B D$ 上找出一点N，使点N是 $B D$ 的一个三等分点．

查看试题解析
18. 如图，在平行四边形ABCD中，点E在边BC上，连结AE并延长，交对角线BD于点F、DC的延长线于点G．如果 $\frac{C E}{B E} = \frac{2}{3}$ ，求 $\frac{F E}{E G}$ 的值．

查看试题解析
19. 某校合唱团组织开展“百人唱红歌”活动，需要发展新合唱团成员，A、B、C、D四名同学均报名参加了应聘，其中A、B来自七年级，C、D来自八年级，张老师、王老师现对这四名同学进行面试．

(1)、若张老师随机抽取一名同学进行面试，恰好抽到C的概率为；

(2)、若以上四位同学随机平均分配到以上两位老师处进行面试，每位老师各面试两人，请用列表法或树状图求来自七年级的A、B两位同学在同一位老师处面试的概率．

查看试题解析
20. 如图，△ABC中，AB＝BC，过A点作BC的平行线与∠ABC的平分线交于点D，连接CD．

(1)、求证：四边形ABCD是菱形；

(2)、过点D作AC的平行线交直线BC于点E，连接DE，点P是线段BD上的动点，若 $A D = 5 ， A C = 2 \sqrt{5}$ ，请直接写出PC+PE的最小值．

查看试题解析
21. 某店销售A产品，每千克售价为100元．

(1)、若连续两次降低售价后，每千克81元，求这两次降价的平均百分率？

(2)、若按现价销售，每千克可以盈利20元，每天可以售出120千克．调查发现，在进价不变的情况下，每千克A产品的售价每涨价2元，日销售量就减少10千克．该店希望每天A产品盈利2340元，设每千克A产品涨价x元（x＞0），求x的值．

查看试题解析
22. 如图，矩形 $E F G H$ 的顶点E，G分别在菱形 $A B C D$ 的边 $A D$ ， $B C$ 上，顶点F，H在菱形 $A B C D$ 的对角线 $B D$ 上．

(1)、求证： $B G = D E$ ；

(2)、若E为 $A D$ 中点， $F H = 2$ ，求菱形 $A B C D$ 的周长．

查看试题解析
23. 我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用．
例：已知x可取任何实数，试求二次三项式 $x^{2} + 6 x - 1$ 最小值．
解： $x^{2} + 6 x - 1 = x^{2} + 2 \times 3 · x + 3^{2} - 3^{2} - 1$
$= {(x + 3)}^{2} - 10$
∵无论x取何实数，总有 ${(x + 3)}^{2} \geq 0$ ．
∴ ${(x + 3)}^{2} - 10 \geq - 10$ ，即 $x^{2} + 6 x - 1$ 的最小值是 $- 10$ ．
即无论x取何实数， $x^{2} + 6 x - 1$ 的值总是不小于 $- 10$ 的实数．
问题：

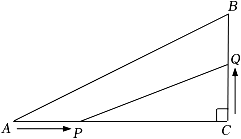
(1)、已知 $y = x^{2} - 4 x + 7$ ，求证y是正数；

(2)、知识迁移：如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 6 c m$ ， $B C = 4 c m$ ，点P在边 $A C$ 上，从点A向点C以 $2 c m / s$ 的速度移动，点Q在 $C B$ 边上以 $\sqrt{3} c m / s$ 的速度从点C向点B移动若点P，Q同时出发，且当一点移动到终点时，另一点也随之停止，设 $△ P C Q$ 的面积为 $S c m^{2}$ ，运动时间为t秒时S最大，请求出t和S的值，

查看试题解析