江西省赣州市定南县2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图标中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知一元二次方程x²+kx-3=0有一个根为1，则k的值为（）

A、−2 B、2 C、−4 D、4

查看试题解析
3. 抛物线 $y = x^{2} - 6 x + 4$ 的顶点坐标是（）

A、 $(3 ， 5)$ B、 $(- 3 ， 5)$ C、 $(3 ， - 5)$ D、 $(- 3 ， - 5)$

查看试题解析
4. 如图，△ODC是由△OAB绕点O顺时针旋转31°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠DOB的度数是（）

A、34° B、36° C、38° D、40°

查看试题解析
5. 某市“菜篮子工程”蔬菜基地2018年产量为100吨，预计到2020年产量可达121吨．设该基地蔬菜产量的年平均增长率为x，则可列方程为（）

A、100（1+x）²＝121 B、121（1-x）²＝100 C、100（1+2x）＝121 D、100（1+x²）＝121

查看试题解析
6. 如图，抛物线 $y = a x^{2} + b x + c$ 的对称轴是 $x = - 1$ ，且过点 $(\frac{1}{2} ， 0)$ ，有下列结论：① $a b c > 0$ ；② $a - 2 b + 4 c = 0$ ；③ $3 b + 2 c > 0$ ；④ $a - b \geq m (a m - b)$ ；其中正确的结论为（）

A、①② B、②③ C、③④ D、①④

查看试题解析

二、填空题

7. 抛物线 $y = 2 x^{2}$ 的图象的对称轴是．

查看试题解析
8. 如图∆DEF是由∆ABC绕着某点旋转得到的，则这点的坐标是.

查看试题解析
9. 设 $x_{1} 、 x_{2}$ 是方程 $x^{2} - 3 x + 2 = 0$ 的两个根，则 $x_{1} + x_{2} - x_{1} x_{2} =$ .

查看试题解析
10. 若关于x的一元二次方程kx²+2x+1＝0有实数根，则k的取值范围是．

查看试题解析
11. 已知函数 $y = 3 (x - 2)^{2} + 1$ 图象上有三点 $A (1 ， y_{1})$ 、 $B (4 ， y_{2})$ 、 $C (\sqrt{2} ， y_{3})$ ，试确定 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小．

查看试题解析
12. 如图，菱形ABCD和菱形AEFG开始完全重合，现将菱形AEFG绕点A顺时针旋转，设旋转角∠BAE=α（0°＜α＜360°），则当α=时，菱形的顶点F会落在菱形ABCD的对角线所在的直线上．

查看试题解析

三、解答题

13.

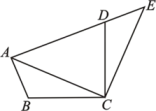
(1)、解方程： $x^{2} + 6 x = - 7$ ；

(2)、如图，将 $△ A B C$ 绕点C顺时针旋转 $90 °$ 得到 $△ E D C$ ．若点A、D、E在同一条直线上，且 $∠ A C B = 20 °$ ，求 $∠ C E A$ 与 $∠ B$ 的度数．

查看试题解析
14. 一道古算题：有执长竿入城门者，横执之多六尺，竖执之多三尺，有老父至，教他斜竿对两角，不多不少刚抵足，借问竿长多少数？
大意如下：某人拿着长竹竿进城门，横着拿竿多六尺，竖着拿竿多三尺，有一个经验丰富的老者，教他斜着拿竹竿进城门，竹竿刚好就是城门斜对角线的长度，正好可以进城，问竹竿长多少尺？（城门为矩形）

查看试题解析
15. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别为A $(1 ， 3)$ ， B $(2 ， 1)$ ， C $(5 ， 2)$ ．
⑴将 $△ A B C$ 以原点O为旋转中心旋转180°得到 $△ A_{1} B_{1} C_{1}$ ，画出旋转后的 $△ A_{1} B_{1} C_{1}$ ．
⑵平移 $△ A B C$ ，使点A的对应点A₂坐标为 $(3 ， - 3)$ ，画出平移后的 $△ A_{2} B_{2} C_{2}$ ．
⑶若将 $△ A_{1} B_{1} C_{1}$ 绕某一点旋转可得到 $△ A_{2} B_{2} C_{2}$ ，请直接写出旋转中心的坐标．

查看试题解析
16. 如图1，某灌溉设备的喷头B高出地面 $1.25 m$ ，喷出的抛物线形水流在与喷头底部A的距离为 $1 m$ 处达到距地面最大高度 $2.25 m$ ，如图2所示建立平面直角坐标系．

(1)、求该抛物线水流对应的二次函数关系式；

(2)、求喷头与水流落地处的水平距离．

查看试题解析
17. 已知 $P = (a - 3 + \frac{9}{a + 3}) \div \frac{a}{a^{2} - 9}$ ．

(1)、化简P；

(2)、若a为方程 $\frac{1}{3}$ x²-x-2=0的解，求P的值．

查看试题解析
18. 已知关于x的方程 $x^{2} + a x + a - 2 = 0$

(1)、当该方程的一个根为1时，求a的值及该方程的另一根；

(2)、求证：不论a取何实数，该方程都有两个不相等的实数根．

查看试题解析
19. 在如图所示的直角坐标系中，已知正方形 $A B C D$ 的边长为 $4$ ，且 $D (2 ， 2)$ ，

(1)、求图像经过 $B$ ， $E$ ， $F$ 三点的二次函数的表达式；

(2)、求（1）中二次函数图象的顶点坐标．

查看试题解析
20. 如图，点 $M$ ， $N$ 分别在正方形 $A B C D$ 的边 $B C$ ， $C D$ 上，且 $∠ M A N = 45 °$ ，把 $△ A D N$ 绕点 $A$ 顺时针旋转 $90 °$ 得到 $△ A B E$ ．

(1)、求证： $△ A E M$ ≌ $△ A N M$ ．

(2)、若 $B M = 3$ ， $D N = 2$ ，求正方形 $A B C D$ 的边长．

查看试题解析
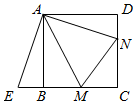21. 在疫情期间，某地推出线上名师公益大课堂，为广大师生、其他社会人士提供线上专业知识学习、心理健康疏导.参与学习第一批公益课的人数达到2万人，因该公益课社会反响良好，参与学习第三批公益课的人数达到2.42万人.参与学习第二批、第三批公益课的人数的增长率相同.

(1)、求这个增长率；

(2)、据大数据统计，参与学习第三批公益课的人数中，师生人数在参与学习第二批公益课的师生人数的基础上增加了80%；但因为已经部分复工，其他社会人士的人数在参与学习第二批公益课的其他社会人士人数的基础上减少了60%.求参与学习第三批公益课的师生人数.

查看试题解析
22. 如图，在正方形ABCD中，E为CD边上一点，以DE为边向外作正方形DEFG，将正方形DEFG绕点D顺时针旋转，连接AG．

(1)、如图1，若AD＝2 $\sqrt{3}$ 、DE＝2，当 $∠ A D G ＝ 150 °$ 时，求AG的长；

(2)、如图2，正方形DEFG绕点D旋转的过程中，取AG的中点M，连接DM、CE，猜想：DM和CE之间有何等量关系？并利用图2加以证明．

查看试题解析
23. 如图，抛物线 $y = - x^{2} + 2 x + 3$ 与 $x$ 轴相交于A、B两点（点A在点B的左侧），与 $y$ 轴相交于点 $C$ ，顶点为 $D$

(1)、直接写出 $A$ 、 $B$ 、 $C$ 三点的坐标和抛物线的对称轴；

(2)、连接 $B C$ ，与抛物线的对称轴交于点 $E$ ，点 $P$ 为线段 $B C$ 上的一个动点，过点 $P$ 作 $P F ∥ D E$ 交抛物线于点 $F$ ，设点 $P$ 的横坐标为 $m$ ；
①用含 $m$ 的代数式表示线段 $P F$ 的长，并求出当 $m$ 为何值时，四边形 $P E D F$ 为平行四边形？
②设 $△ B C F$ 的面积为S，求S与 $m$ 的函数关系式

查看试题解析