河北省唐山市丰南区2021-2022学年九年级上学期期中数学试卷

试卷更新日期：2022-12-09 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程 $3 x^{2} = 3 - 2 x$ 的一次项系数和常数项分别是（）

A、2和-3 B、3和-2 C、-3和2 D、3和2

查看试题解析
2. 以下关于新型冠状病毒的防范宣传图标中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 已知点 $A (- 2, a)$ ， $B (2, b)$ ， $C (4, c)$ 是抛物线 $y = x^{2} - 4 x$ 上的三点，则a，b，c的大小关系为（）

A、 $b > c > a$ B、 $b > a > c$ C、 $c > a > b$ D、 $a > c > b$

查看试题解析
4. 若关于x的一元二次方程 $(a - 2) x^{2} + 4 x + a^{2} - 4 = 0$ 的常数项为0，则a的值为（）

A、2 B、-2 C、±2 D、0

查看试题解析
5. 对于二次函数y＝﹣ $\frac{1}{4}$ （x﹣2）²﹣3，下列说法正确的是（）

A、当x＞2时，y随x的增大而增大 B、当x＝2时，y有最大值﹣3 C、图象的顶点坐标为（﹣2，﹣3） D、图象与x轴有两个交点

查看试题解析
6. 如图，将△ABC绕点A逆时针旋转100°，得到△ADE，若点D在线段BC的延长线上，则∠B的大小为（）

A、 $6 0^{∘}$ B、 $5 0^{∘}$ C、 $4 5^{∘}$ D、 $4 0^{∘}$

查看试题解析
7. 代数式 $3 x^{2} - 4 x + 6$ 的值为9，则 $x^{2} - \frac{4}{3} x + 6$ 的值为（）

A、 $7$ B、 $18$ C、 $12$ D、 $9$

查看试题解析
8. 如图，是二次函数 $y = a x^{2} + b x + c$ 的图象，则下列四个结论中正确的有（）
① $a b c ＜ 0$ ；② $b^{2} ＞ 4 a c$ ；③ $2 a + b = 0$ ；④ $9 a + 3 b + c ＞ 0$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 一块矩形菜地的面积是120平方米，如果它的长减少2米，菜地就变成正方形，则原菜地的长是（）

A、10 B、12 C、13 D、14

查看试题解析
10. 函数y=ax²+2ax+m（a＜0）的图象过点（2，0），则使函数值y＜0成立的x的取值范围是（）

A、x＜﹣4或x＞2 B、﹣4＜x＜2 C、x＜0或x＞2 D、0＜x＜2

查看试题解析
11. 一个 $Q Q$ 群里共有 $x$ 个好友，每个好友都分别给群里的其他好友发一条信息，共发信息1980条，则可列方程（）

A、 $\frac{1}{2} x (x - 1) = 1980$ B、 $x (x - 1) = 1980$ C、 $\frac{1}{2} x (x + 1) = 1980$ D、 $x (x + 1) = 1980$

查看试题解析
12. 嘉琪在距离地面 $2 m$ 高的房顶把一圆球以初速度 $v_{0}$ （ $m$ / $s$ ）竖直向上抛出，在不计空气阻力的情况下，其上升高度 $s$ （ $m$ ）与抛出时间 $t$ （ $s$ ）满足： $s = v_{0} t - \frac{1}{2} g t^{2}$ （其中 $g$ 是常数，通常取 $10 m$ / $s^{2}$ ）．若 $v_{0} = 10 m$ / $s$ ，则该物体在运动过程中最高点距地面（）

A、 $2 m$ B、 $5 m$ C、 $7 m$ D、 $10 m$

查看试题解析
13. 如图，点E是正方形 $A B C D$ 的边 $D C$ 上一点，把 $△ A D E$ 绕点A顺时针旋转 $90 °$ 到 $△ A B F$ 位置．若四边形 $A E C F$ 的面积为36， $D E = 2$ ，则 $A E$ 的长为（）

A、 $4 \sqrt{2}$ B、 $2 \sqrt{6}$ C、6 D、 $2 \sqrt{10}$

查看试题解析
14. 在平面直角坐标系中，有两条抛物线关于x轴对称，且它们的顶点相距8个单位长度．若其中一条抛物线的函数表达式为 $y = x^{2} - 6 x + m$ ，则m的值是（）

A、-5或-13 B、-1或19 C、5或13 D、4或14

查看试题解析
15. 已知一次函数 y=kx+b 的大致图象如图所示，则关于 x 的一元二次方程 x²-2x+kb+1=0 的根的情况是（）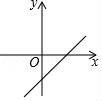

A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、有一个根是 0

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $A C$ 是对角线，将矩形 $A B C D$ 绕点 $B$ 顺时针旋转 $90 °$ 到 $G B E F$ 位置， $H$ 是 $E G$ 的中点，若 $A B = 6$ ， $B C = 8$ ，则线段 $C H$ 的长为（）

A、 $2 \sqrt{5}$ B、6 C、5 D、 $\sqrt{41}$

查看试题解析

二、填空题

17. 将方程 $(3 - 2 x)(x +2) = 5$ 化为一般形式为．

查看试题解析
18. 若抛物线y＝2x²-mx+n向上平移2个单位长度，再向左平移3个单位长度得到抛物线y＝2x²-4x+1，则m＝， n＝．

查看试题解析
19. 第一次：将点A绕原点O逆时针旋转 $90 °$ 得到 $A_{1}$ ；
第二次：作点 $A_{1}$ 关于x轴的对称点 $A_{2}$ ；
第三次：将点 $A_{2}$ 绕点O逆时针旋转 $90 °$ 得到 $A_{3}$ ；
第四次：作点 $A_{3}$ 关于x轴的对称点 $A_{4}$ …，
按照这样的规律，点 $A_{3}$ 的坐标是，点 $A_{2021}$ 的坐标是．

查看试题解析

三、解答题

20. 已知关于x的一元二次方程 $x^{2} - (2 k + 1) x + \frac{1}{2} k^{2} - 2 = 0$ ．

(1)、求证：无论k为何实数，方程总有两个不相等的实数根；

(2)、若这个方程有一个根为1，求k的值．

查看试题解析
21. 如图是二次函数 $y = a x^{2} + b x + c$ 的图象，与x轴交于B，C两点，与y轴交于A点．

(1)、如果A点的坐标为 $（ 0 ， - 3 ）$ ， $∠ A B C = 45 °$ ， $3 O C = O A$ ，求这个二次函数的函数表达式．

(2)、点P在（1）中的抛物线上，且 $S_{△ B C P} = \frac{4}{3} S_{△ A B C}$ ，求P点坐标．

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A C = B C = 3 \sqrt{2}$ ，点D在 $A B$ 上，且 $B A = 3 A D$ ，连接 $C D$ ，将线段 $C D$ 绕点C逆时针方向旋转 $90 °$ 至 $C E$ ，连接 $B E ， D E$ ．

(1)、求证： $△ A C D ≌ △ B C E$ ；

(2)、求线段 $D E$ 的长度．

查看试题解析
23. 某超市服装柜在销售中发现：进货价为每件50元，销售价为每件90元的某品牌服装平均每天可售出20件，现商场决定采取适当的降价措施并规定：单件获利不超过50%．经市场调查发现：如果每件服装降价0.5元，那么平均每天就可多售出1件．设每件服装降价x元．

(1)、用含x的代数式表示降价后平均每天销售的数量；

(2)、要想平均每天销售这种服装盈利1200元，那么每件的售价应为多少？

查看试题解析
24. 把一副三角板按如图甲放置，其中∠ACB＝∠DEC＝90°，∠A＝45°，∠D＝30°，斜边AB＝6cm，DC＝7cm．把三角板DCE绕点C顺时针旋转15°得到△D₁CE₁（如图乙）．这时AB与CD₁相交于点O、与D₁E₁相交于点F．

(1)、求∠OFE₁的度数；

(2)、求线段AD₁的长；

(3)、若把△DCE绕着点C顺时针再旋转30°得△D₂CE₂ ，这时点B在△D₂CE₂的内部、外部、还是边上？说明理由．

查看试题解析
25. 如图，足球场上守门员在 $O$ 处开出一高球，球从离地面1米的 $A$ 处飞出（ $A$ 在 $y$ 轴上），运动员乙在距 $O$ 点6米的 $B$ 处发现球在自己头的正上方达到最高点 $M$ ，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．

(1)、求足球开始飞出到第一次落地时，该抛物线的表达式．

(2)、足球第一次落地点 $C$ 距守门员多少米？（取 $4 \sqrt{3} = 7$ ）

(3)、运动员乙要抢到第二个落点 $D$ ，他应再向前跑多少米？
（取 $2 \sqrt{6} = 5$ ）

查看试题解析
26. 如图，在平面直角坐标系 $x O y$ 中，A、B为x轴上两点，C、D为y轴上的两点，经
过点A、C、B的抛物线的一部分C₁与经过点A、D、B的抛物线的一部分C₂组合成一条封闭曲线，我们把这条封
闭曲线称为“蛋线”．已知点C的坐标为（0，），点M是抛物线C₂： $y = m x^{2} - 2 m x - 3 m$ （ $m$ ＜0）的顶点．

(1)、求A、B两点的坐标；

(2)、“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；

(3)、当△BDM为直角三角形时，求 $m$ 的值．

查看试题解析